混沌系统变量的分离时间能够反映系统参数的近似程度,这为参数探测和同步攻击的实施提供了便利。针对这个混沌系统所共有的安全弱点,通过预处理系统变量并对系统参敦扰动,得到了对参数偏盖敏感且分离时阀与参敦差值关东不明显的混沌变量,随后,提出了一种时变密钥自同步混池加密方法,该方法具有抵御同步攻击的能力,可以实现一次一密的安全思想。安全性分析和仿真实验证明了谊方法的可行性和安全性。
一、混沌参数敏感性分析
设n维系统:
![]()
其中,n维向量函数f(x)的各元素,fi(x),i=1,2,...,n是x的有界、连续可微单值函数。设参数向量a∈Rm使系统(1)处于混沌态,a和初值x0组成向量ψd=[a,x0]t,ψd∈Rm+n。
系统(1)的同构系统为:
![]()
同理有参数向量β∈Rm与初值y0的组合向量ψr=[β,y0]t,ψr∈Rm+n。
定义1:设系统(1)和(2)在初始状态xo,y0下的解x(t)=φ(t;to,xo),y(t)=φ(t;to,yo),满足Lipschitz条件。若系统(1)与(2)的同步误差:
![]()
满足:
![]()
其中![]() 是欧几里德范数,称系统(1)与(2)同步。当初值满足xo,yo∝D(t0),称D(t0)为同步区域。
是欧几里德范数,称系统(1)与(2)同步。当初值满足xo,yo∝D(t0),称D(t0)为同步区域。
定义2:令系统(1)和(2)的ψd,ψr存在微小偏差:
![]()
其中,l为大于零的整数。若同步误差τ在经过时间τ(τ>to),达到稳态后的范数满足:
![]()
其中,L (L>0)是预先设定的轨道分离的下确界,则称混沌系统(1)与(2)的轨道完成分离,并称τ为系统(1)和(2)的参数或初值偏差为z级时的分离时间。
分离时间T描述了参数(或初值)存在偏差的同构混沌系统变量的分离速度,τ越小分离速度越快,系统变量对参数(或初值)的敏感度也越高,越能够提供高的安全特性。
考虑处于混沌态的Lorenz系统

构造非耦合同构系统,令初值相同而参数存在偏差,即![]() ,取L =10-4,则I与T的关系如图1所示:
,取L =10-4,则I与T的关系如图1所示:

图1曲线说明了Lorerrz系统变量的分离时间与参数的偏差量级数存在明显对应关系,特别在参数偏差较小时分离时间较长,这都为参数探测和同步攻击的实施提供了条件。实验表明Rosslor系统、细胞神经网络(CNN)系统以及Logstic等混沌系统都存在此类问题,是混沌系统存在的一个共同安全弱点。
二、参数敏感性改善方法
定义3:对于n维系统(1),当参数向量Ⅱ取值Q击时系统为混沌状态。如果对于任意给定的实数e>0,使得参数向量满足|a一ach|≤θ时,系统(1)仍为混沌的,则称e为系统(1)的混沌参数范围。
设混沌系统参数向量as(t),as∈Rm为:
![]()
当满足||μ(x) ||<θ时,θ是系统的混沌参数范围,称as(t) 为混沌时变参数向量μ(x)为变量预处理函数。
取x为lorerrz系统变量的函数,令μ(x)为:
![]()
其中,![]() 为取整运算。
为取整运算。
构造两Lorenz同构系统,令初值相同而参数存在偏差![]() ,改变定值参数a2为时变参数:
,改变定值参数a2为时变参数:
![]()
其中,w2= 102。在v=0(无时变)时依据式(9)得到变量Xsl,v=0.1时得到变量X/2,取L=10-4,则变量X1,Xsl,Xs2相对应的Z与T关系曲线如图2所示。
由图2可知,当系统参数取固定值时(V=0),Xs1对参数变化的敏感性要好于X1,而当参数为时变时(V=0.1),得到的混沌变量X对参数变化敏感性较好,对应变量分离时间与参数差值的关系不明显,且具有近似均匀性,因此Xs2更适合作为明文信息的调制变量。
三、时变密钥混沌加密系统
1、系统设计
密码学中用密钥长度表示安全程度,在混沌同步保密通信中,混沌系统的参数和初值相当于密钥。根据Shanron的信息理论,“一次一密’’是最安全的,如果混沌系统的参数或初值是某种程度上的随机变量,将可能取得近似“一次一密”的效果。利用式(8)得到时变参数时,是充分利用了混沌系统自身的内随机特性,通过函数μ()产生伪随机变量叠加到混沌系统参数上,形成了一种具有伪随机特性的动态密钥。据此,可设计一种时变密钥混沌加密系统,其结构如图3所示。

图3中x为Lorenz变量,b为对xs量化生成二值伪随机序列,m为明文,c为密文,加解密采用二值异或方式;x’为接收端为Lorertz变量,b'为接收端量化二值伪随机序列,m'为解密明文。Xsyn为同步信号,Xsyn为定时采集的LorerTz系统变量值。发送控制器则负责将定时采集的同步信息Xsyn按一定字长对其编码与密文c按照一定格式连接发送给接收端。接收控制器负责将同步信号Xsyn和密文c分离,利用Xsyn定时驱动接收端系统,迫使其与发送端同构混沌同步使得b'=b(参数相同时)以实现对密文的解密。
2、可行性与安全性分析
当接收端的参数设置与发送端一致时,由于同步信息Xsyn直接将接收端当前系统状态值替换,接收端在下一步迭代时会产生与发送端相同的状态变量,即x’=x,从而得到x’s=xs。在相同烁作用下,接收端系统参数也跟随发送端变化,生成b'=b,可得到m'=m。同步信息Xsyn是定时发送的,即使在异步接收情况下也能正确解密。
为增加实用性,同步信息Xsyn大都以明文传递,攻击者可利用Xsy。驱动本地系统实现同步攻击。而在本系统中,用于加密的二值序列来源于对参数变化敏感的变量xs,攻击者可利用实施同步攻击的时间很短。同时由于μ(x)作为随机扰动加入到收发双方混沌系统中,参数是时变的,攻击者即使得到某时刻精确参数值,仍然无法对随后的密文解密。
四、仿真分析
采用Lorenz系统变量X1作为被处理变量,取w=100,按照式(9)得到xs。X1,xs波形如图4所示,相关特性如图5和图6所示,可见xs性明显优于X1,更适合生成用于加密的二值伪随机序列。

设明文信息为正弦信号的二值编码,同步信息为Xsyn=[X1syn,X2syn,X3syn],即同步信息为定时提取的3个变量的数值,则不同情况下的加解密测试如图7所示,正确解密时接收端晚于发送端200步,错误解密时参数差为![]()

小知识之欧几里得范数
欧几里得范数即欧几里得度量,欧几里得空间中,点 x = (x1,...,xn) 和 y = (y1,...,yn) 之间的距离为
向量 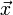 的自然长度,即该点到原点的距离为
的自然长度,即该点到原点的距离为
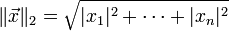 .
.
它是一个纯数值。在欧几里得度量下,两点之间直线最短。










