图像文件加密之变参数混沌系统加密

针对一维离散单混沌系统在计算机有限精度下存在的退化问题，提出了一种在生成混沌信号的过程中参数随机变化的混沌伪随机序列产生方法，基于该方法构建的混沌系统较单混沌系统具有伪随机序列周期大、密钥数量多、密钥空间大等优势，所产生的密码具有更高的安全性能。

一、参数随机变化的一维混沌映射

通过随机改变混沌映射的参数，可以提高混沌序列的复杂性，并且在有限精度实现时，使得混沌序列的周期可用不同参数的混沌映射的数目来度量，即混沌序列的周期等于状态x（i）的周期与参数的周期的乘积。

1、一个良好随机统计特性的分段线性混沌映射PLCM

一个良好随机统计特性的一维分段线性迭代混沌映射，其定义如下：

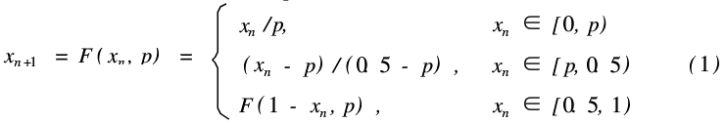
其中，x∈(0,1]，p∈(0,0.5)。

该迭代系统是混沌的，其输出信号，{x(t)}在[o，1]上遍历，且具有良好的自相关性和均匀分布特性。

2、Logistic混沌映射

其中，O≤Xn≤1，n∈Z当μ∈[3.57，4]时，系统是混沌的。

若直接利用式(1)的迭代来产生密钥序列存在混沌参数p易被破解的缺陷。

对于由式(1)生成的混沌序列，只要得到位于同一个分段上的任意两个（或多个）的点对x(t)，x(t+1)、x(t')，x(t'+1)，就能确定出参数：

3、参数随机变化的多级一维分段线性混沌系统

基于FLCM和Logistic混沌映射，本文设计了一个基于参数随机变化的多级混沌系统。如图1所示。

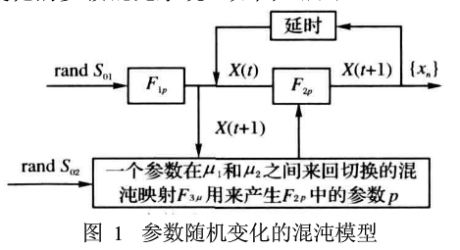
其中，S01，S02是用户随机输入的初始条件，Fip是一个按式(1)定义的一维分段线性混沌映射fLCM迭代k次后的混沌映射，其表达式为x(i+1)=fk(x(i)，p)，其中k>n，
k为迭代级数，FIP的初始值是用户随机输入的S01，利用S01作为Fi，的初始条件来生成x(1)。F1p，用来控制F2p的初始化和迭代过程，其中F2p是按式(1)定义的一个一维分段线性混沌映射PLCM。由于是在有限精度下实现，所以设其精度为n，则序列{x(t)}t=1的取值空间为2n。

F2p也是一个一维线性混沌映射PLCM，在n=16精度下，由于参数p的取值空间为216所以对不同的参数另F2p可以看成是不同的混沌模型。也即相当于存在216个一维线性
混沌映射F(x，p)。在每次迭代的过程中，F，中的控制参数p是这样产生的。

1)初始时，随机输入一个数据O1时，p=F3μ(x(t-1)，μ)／3，其中μ=μ1或μ2。

3)F3μ中的参数μ是这样控制在μ1和μ2之间来回切换的：把迭代次数徐运算正整数m，当运算结果为奇数时，F中使用参数μ1，当运算结果为偶数时，F3μ中使用参数μ2。

这就保证了在生成，{x(t)}t=1的过程中，当某次迭代产生的x(t')与之前的某次x(t)相等时其中t’>t与x(t')对应的参数p'也以极大的概率与x(t')对应的参数p不相等。只有当某次的迭代状态与之前的相同而且要使其对应的参数也与之前的相同时，混沌序列才会出现循环。在该伪随机序列发生器中，只有当x(t-1)与x(t'-1)相等，x(t)与x(t')相等，而且还必须当tm与t'%m运算得到的这两个数的奇偶性相同时，该伪随机序列才可能会进入周期循环之中。这样，混沌序列的周期即h=t*22n，其中n为精度，h=1，2，3，4，…，h的初始值和m有关。从而在有限精度实现时，输出混沌序列的周期变大，并可以度量。

二、序列转换为0-1序列

把根据图1生成的模拟序列{x(t)}t=1用量化函数进行量化，得到0-1二进制序列{s(t)}t=1：

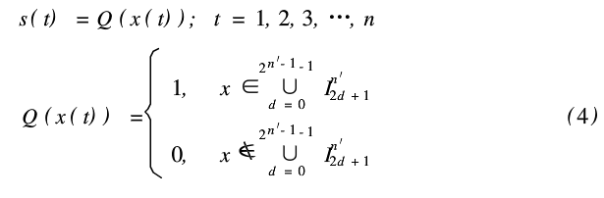
其中，ni为任意正整数，I0n'，I1n'，I2n'，I3n'，一是区间，o，1的2n'个连续的等分区间。

由于混沌序列，{x(t)}t=1具有良好的随机统计特性，这样生成的{s(t)}t=1在理论上具有均衡的0-1比和δ-like的自相关等优良的统计特性。

最后，为了进一步增加算法的随机性，提高序列的抗破解能力，使得对初始条件的攻击无效，加密时截掉序列的初始端部分和结尾部分，假设序列{s(t)}t=1L的长度为L，任取截点N1，N2，满足1<N1

这样，本算法的保密性不但依赖于混沌系统的参数和初始条件，而且还依赖于保密系统的初始值N1，N2和随机选取的某个正整数m，m=1，2 3，4，5，…。这样，加密系统的密钥就包括N1，N2，m，n'，s01，S02，p，p1～p(2n)，L1，L12，这就使得密码分析变得极其困难。

三、混沌系统性能分析

本文设计的混沌系统有以下优点。

1)保证了产生的0-1序列满足二值分布。在迭代过程中，每次换一个混沌参数p(t)，相当于更换了一个混沌方程。由此来提高产生的混沌序列的复杂性，而且对于相同的状态p(t)，由于它所对应的参数p(t)不同，使得它的下一个状态x(t+1)不同。

2)使得破解参数p变得异常复杂。破解一个一维分段线性混沌的参数p需要该混沌2个点对。本系统有2n个不同的混沌方程。所以一个点对落入一个指定的混沌的概率为2n，2个点对同时落入一个指定的混沌方程的概率为2-n X2-n=2-2n，因此，破解本系统的一个混沌参数的复杂度是破解一维分段线性混沌映射的22n倍。全部破解P1，p2，p3，…，p2n。这2n个参数，其复杂度是破解一维分段线性混沌系统的2n*22n=23n倍。同时由于N1，N2，m的引入，破解该混沌系统的复杂度在此基础上又得到了极大的提高，使得到的混沌序列的随机性更强，周期更长，极大地增强了抗密码分析的能力。

3)进一步增大了序列的周期。作为密码序列，其周期应该越长越好。而定参数的方法产生的序列的周期完全取决于序列{x(i)}的精度。而本文采用的方法其周期由混沌参数的改变周期与，{x(i)}的周期的乘积来决定，即，h X2n×2n=7z×22n（n为数字化精度，h为正整数），这样产生的序列周期大大增加,而且可以度量。

四、变参数混沌系统的仿真验证

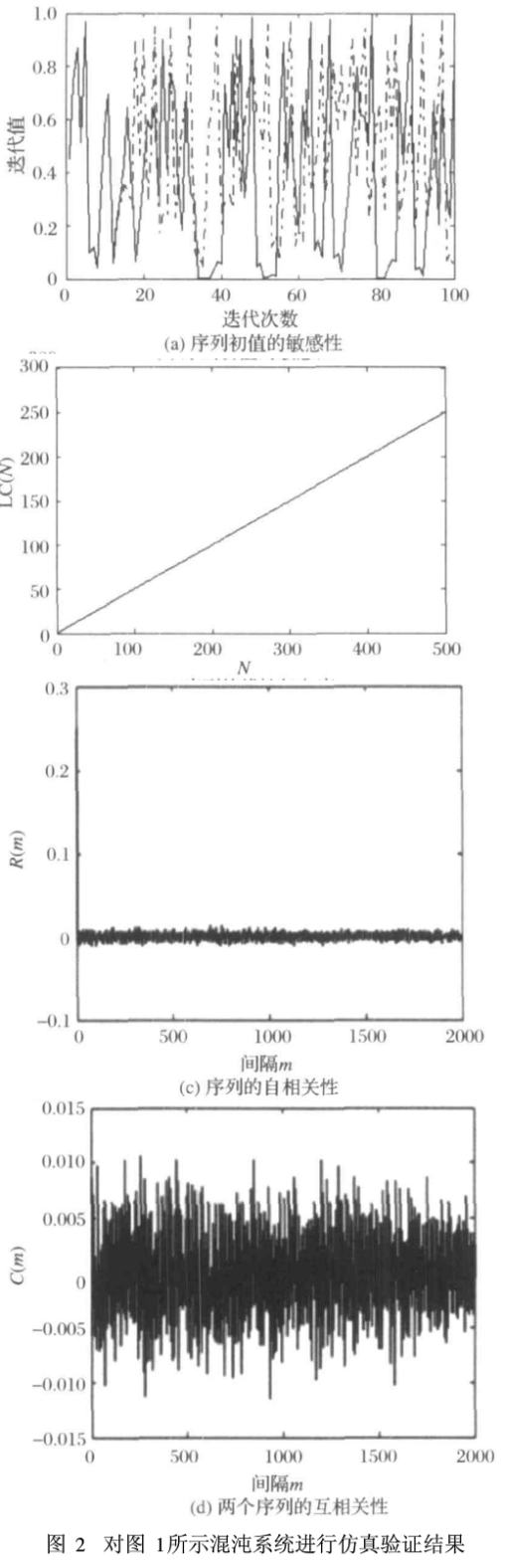
从图2(a)可以看出，该混沌系统在初始值S01改变10- 16时，该混沌系统大约经历15次迭代之后，这两个序列就变得完全不同了，其中，实线为初值So1=9.501292851471754e -001，虚线为初值So1 =9. 501292851471753e - 001，这说明该伪随机序列发生器对初始值具有极高的敏感性。由 Berlekanp Messy算法对该序列的线性复杂度进行分析，可从图2(b)看出，该序列的线性复杂度曲线趋向于独立二项同分布随机序列的复杂度曲线，约等于序列长度的一半，表现出良好的随机性，满足保密通信的要求。从图2(c)、(d)可以看出，该伪随机数发生器生成的二进制混沌序列，{k(t)}t=1具有类似δ-like的性质，有尖锐的自相关和良好的互相关性。

五、基于该混沌系统的图像加密算法

1、图像加密解密算法原理

加密算法

1)发送方利用该混沌模型在本地生成加密序列fo（假定图像大小为M×M，灰度等级为256，则序列肭长度为M×MX8；如果数字图像不是方阵，可以通过填充为背景色的方法扩充为方阵。为了提高加密／解密效率，序列f可以多次使用，发送方和接收方经过协商可以在约定时刻更换加密序列Z以提高加密算法的安全性。)

2)发送方通过初始值S01、S02和混沌参数利用该混沌模型生成一个序列，把该序列量化为0-1序列后，转换为一个十进制数组x（L)，且L≤Mo用x（L)对图像的灰度矩阵m进行行置乱，即根据x（L)中的元素值对m的相应于该值的行进行倒置，得到m2。

3)同2)，发送方利用该混沌模型最终生成一个十进制数组Y(L2)，且L2≤M。用Y(L2)对经过第2)步后图像的灰度矩阵m2进行列置乱，即根据Y(L2)中的元素值对m2的相应于该值的列进行倒置，得到m3。

4)发送方利用该混沌模型最终生成一个十进制数组Z(L3)，且L3≤M。通过Z(L3)，对m3以主对角线为对称轴，把按Z(L3)指定的那些平行于主对角线的行进行翻转，得到
m4。

5)同4)，发送方生成十进制数组N(L4)，且L4≤M。通过N(L4)，对m4以副对角线为对称轴，把按w(L4)指定的那些平行于副对角线的行进行翻转，得到最终置乱后的矩阵
m5。

6)用第1)步生成的加密序列f对m5转换成的二进制位进行逐位异或运算。得到加密后的图像。

7)发送方把生成该混沌模型加密序列J各个初始值和参数以及生成x(L)、y(L2)、Z(L3)、w (L4)的各个初始值和参数在一个安全信道上传给接收方。

8)发送方把加密后的图像通过公共信道传给接收方。

2、算法安全性分析

1)从算法的原理看，整个算法由两部分组成：置乱和替代。这与很多图像加密算法原理相似，不同的是，一般的图像加密算法中置乱矩阵时不受密钥的控制，导致无法完全公开加密算法，不能抵御选择明文攻击，而本算法在对灰度矩阵置乱时要4次用到混沌系统产生的混沌序列，即要受到密钥的控制，而且本系统密钥数量众多；此外，以本文中大小为256×256的灰度矩阵为例，完全能够抵御穷举攻击，这就极大地增加了加密图像的抗破解性。

2)该加密方案利用本文中提出的混沌系统产生的混沌序列作为加密序列，利用了该混沌系统对初始条件的极端敏感性，对于初始值仅有非常微小的偏差，该混沌系统在迭代了一定的次数后便会产生完全不同的混沌序列，本文中混沌系统由于使用的是迭代2000次之后的混沌序列，使得加密效果更佳，安全性更高。

3)由于本文采用的混沌系统是有多个混沌映射级联而成，这就大大增大了密钥的个数和密钥空间；从一次一密的角度分析，加密者可以随意地选择密钥，这极大地增强加密后图像抵抗强行攻击的能力；同时，该混沌系统设计原理简单，便于用硬件实现。

六、加密仿真及安全性分析

1、可视效果及对密钥的敏感性

采用该加密方案对多幅图像进行了实验，图3为用该方案对大小为256*256，灰度等级为256的BMP图像Yanhn加密解密的结果。其中，图3(a)为Yanhn原始图像，生成加密序列肭密钥参数为0.45，3 57.3 92, 12.5，5000 +65536×8， So1，So2），其中，S01=9501292851471754e-001. S02=2311385135742878e-001；生成置乱矩阵时所用的密钥参数为：(0.45,3.57,3.67, 11,5,200,4 450 964 322 879468e-001，0.318 145 784 616 647e -001，0.38，0.5,3.97,9,5,210,4659 943 416 754 240e- 001,4 186 494 677 275 062 e-001,0.49,0.82,3.71, 12,7,240，&462214178243245e-001,5.251524963 051724e - 001,0.48,3.73,3.62, 10,5,180,2026473576503873e-001,6 721374684742885e-001);图3(b)为置乱操作后异或加密前图像，图3(c)为加密后图像。图4(a)为使用正确密钥解密后得到的图像。把生成加密序列f的初始密钥S01改为：9.501292851471753e - 001，即S01减小了10-16，其他一切参数都不变，解密后得到的图像为图4(b)；把生成加密序列，的初始密钥S02改为：2311385135742879e-01，即S02增加了10- 16，其他一切密钥参数都同正确的密钥参数相等，解密后得到的图像为图4(c)。从仿真结果可以看出，该混沌系统对密钥参数极其敏感，即使密钥参数发生极其微小的偏差都会造成无法正确解密。

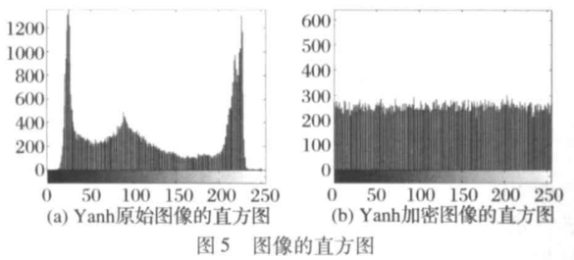
从图5(a) Yanhn原始图像的直方图可以看出，不同像素值的像素数目分布是不均等的；而加密后的直方图图5(b)表明，密文像素值在整个取值空间的取值概率趋于均等，呈现出良好的均匀分布特性，完全掩盖了Yanhn原图的特性。

2、相邻像素的相关性分析

为了检验明文图像和密文图像相邻像素的相关性，从图像中随机选取部分水平方向相邻像素对，部分垂直方向相邻像素对和部分对角线方向相邻像素对，用下列公式定量计算相邻像素的相关系数：

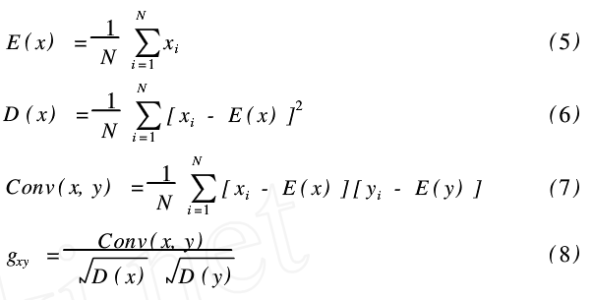
其中，x和y分别表示灰度图像中相邻2个像素的像素值，gxy即为灰度图像中相邻2个像素的相关系数。

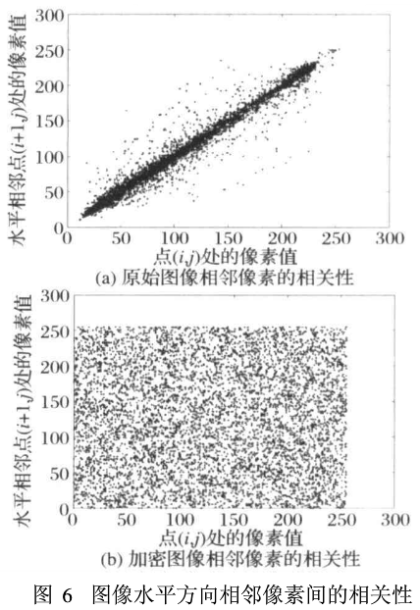
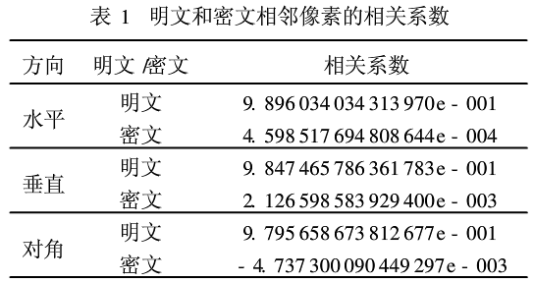
图6所示为原始Yanhn灰度图像相邻像素和加密后Yanhn灰度图像相邻像素的相关性，表1列出了按水平、垂直及对角线3种方向计算所得的图像相邻像素间的相关系数值。可以看出，原始明文Yanhn图像的相邻像素高度相关，相关系数值接近于1；加密后Yanhn图像的相邻像素相关系数接近于0，表明相邻像素已基本不相关，证明图像的统计特征已被扩散到了随机的密文中，能够有效抵御像素相关统计分析攻击。

admin普通用户

海报分享