利用混沌映射具有对初值和系统参数的敏感性以及轨道的不确定性,提出一种基于多个一维混沌映射的加密算法。该加密算法使用线性同余随机数发生器产生混沌映射的系统参数和3个一维混沌映射的使用顺序,同时通过输出反馈方式动态改变混沌映射初值、选代次数以及线性同余随机数发生器参数。
一、混沌加密算法
加密算法的描述:
(1)在加密算法中,128位的密钥被分成多个8bit为单位的块,每块称作会话密钥,进一步将密钥划分成32bit为单位的子密钥kμi,i=l,2,…,4和64 bit为单位的子密钥Ki,i=1,2,它们都是以十六进制来表示的,其划分情况为:
![]()
(2)在加密/解密过程中明文/密文被分成多个8 bit为单位的块,其划分情况分别为:
![]()
(3)在加密/解密过程中选取3个一维混沌映射来进行加密/解密,它们分别是:Logistic映射、帐篷映射、正弦映射,如表1所示。表中第1列为混沌映射名称,第2列是3个混沌映射的编号,第3列是3个混沌映射对应的迭代表达式,第4列是混沌映射系统参数取值范围,该范围表示相应混沌映射处于混沌状态。

(4)开始时由会话密钥和子密钥构造的初始值分别为:
![]()
![]()
随机数由线性同余随机数发生器(LCG)产生:
![]()
式中Yo=[xb×213]。由写产生的混沌映射号从使用会话密钥的顺序号,分别为:
![]()
(5)混沌映射的迭代次数N和初值x分别为:
![]()
根据混沌映射号M的不同取值选择不同的混沌映射系统参数μi,产生式:
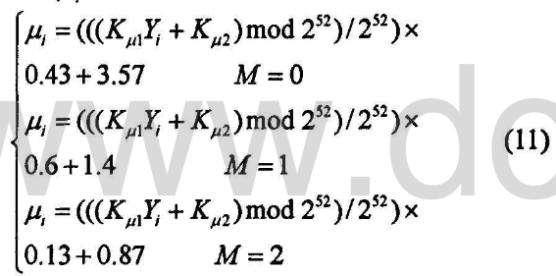
(6)明文/密文每一块被加密/解密,用初值μ1系统参数肛使混沌映射迭代N次。新值X(x’)被用于构造明文/密文以及作为下一步迭代输出反馈的一部分,如下列等式所示:
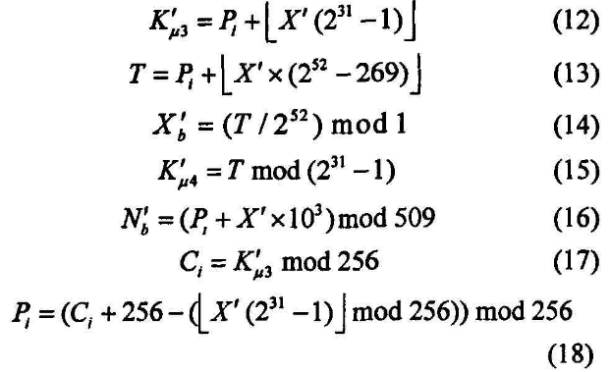
对于加密/解密下一块明文/密文,上一次的Nb'和Xb'分别代替式(9)、式(10)中的Nb和Xb,Kμ3'和Kμ4'分别更新式(6)中的随机发生器参数Kμ3和Kμ4。
加密/解密过程基本相同,唯一不同之处在于加密过程用的是式(17),解密过程用的是式(18)。解密过程先用式(18)求Pi,再用式(12)-式(16)求Kμ3',T、Xb'、Kμ4'、Nb'。
已有资料论证了随机数发生器中乘法器和模的取值问题,由于在式(6)中乘法器是由密钥分离而来,可以不考虑它的取值问题。在式(6)中模取231 -1,因为它是一个奇素数,产生的随机数具有比较大的周期。
由于双精度占64位,其中第1位是符号位,依次是指数位,占11位,剩余的52位是尾数,因此取252作为式(4)、式(11)的模是恰当的,充分保证了系统参数μ1的密钥取值空间,又不会引入小数的不确定位。
二、实验及结果分析
采用以下试验环境:CPU是Intel Celeron处理器,主频为450 MHz:内存为196 MB;操作系统为Windows 2000;使用VC++编程实现本文的算法。
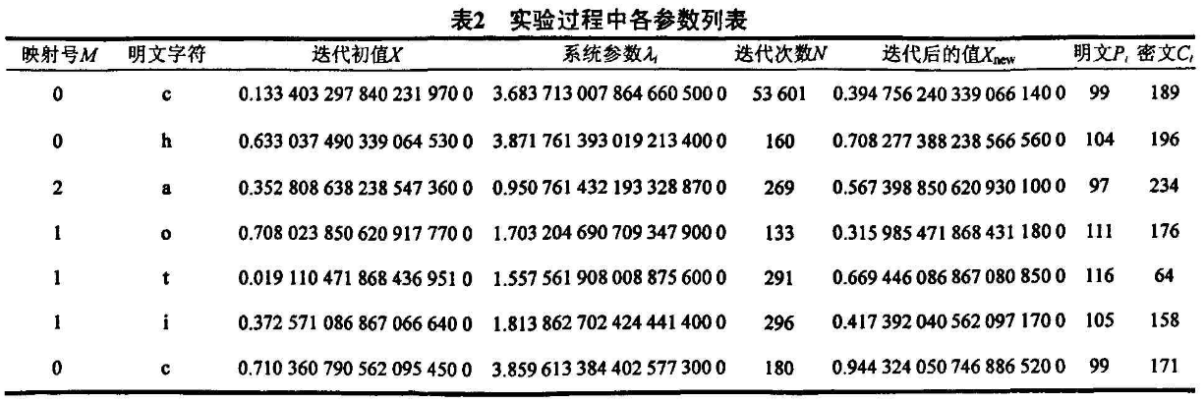
表2为使用密钥“1284A54432FF487C4A923D274C172437”对明文“chaotic"进行加密的过程。整数类型用signcd_int64,小数类型用long double,如果小数类型采用single将使密码空间降低1倍左右。算法设计的目的是使3个混沌映射的系统参数、初值和迭代后的值均平均约有252个取值。
1、统计分析
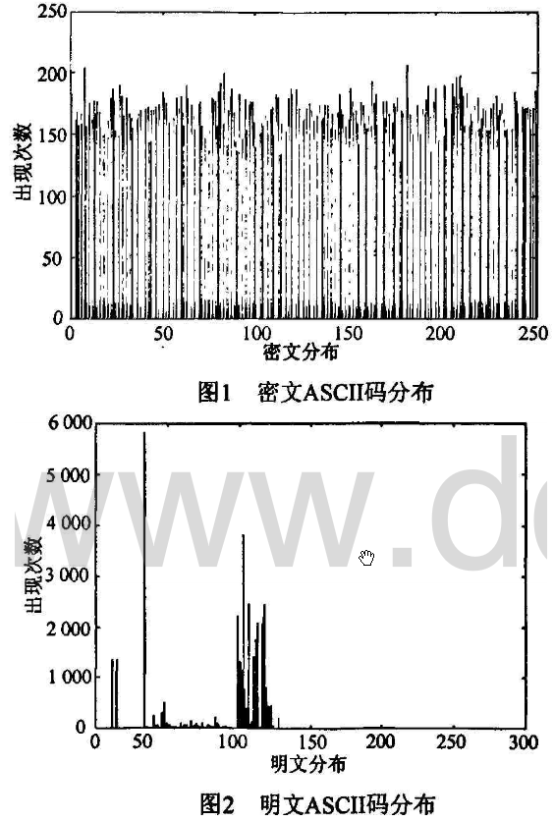
图1表示本文算法加密42kB明文后的密文分布,密文也是42kB,扩展密钥用的是“1284A54432FF487C4A923D274C172437”。很明显,图2中明文大多是一些高频字符,经过加密后密文分布却是平坦的。统计分析经常被用来进行密码分析和破译,好的密码系统不管明文是如何分布的,密文分布应该是均匀的。从图1的密文分布完全能说明本文的算法能有效防止密码分析者利用统计分析的方法来击破整个加密系统。
2、敏感性测试
好的加密系统,其函数必须是复杂的,并且一个小的变化必然导致结果发生很大的变化。图3所示为对明文“chaoticcryptosystemblockcipher"用仅差一位的密钥加密后所得的结果,使用的密钥分别是“1284A54432FF487C4A923D274C172437" 和"1184A 54432FF487C4A923D274C172437"。图中横轴表示序号,纵轴表示对应的ASCII码值,实线连接的点表示明文ASCII分布,点连接的“*”表示使用“1284A54432FF487C4A923D274C172437"作为密钥加密后密文ASCII分布,虚线连接的“+”表示使用“IIB4A54432FF487C4A923D274C172437”为密钥加密后密文ASCII分布。从图中不难看出,虽然密钥仅相差—位,但加密后所得的密文却完全不同,这也说明本文所设计的密码系统对密钥具有敏感性。
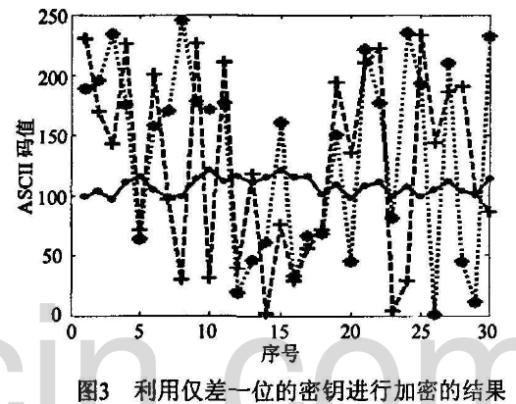
图4是用图3明文变化一个字符,将其最前面字符‘c’变为'a’,密钥仍然使用“1284A54432FF487C4A923D274C172437”加密后所得的结果。图中横轴表示序号,纵轴表示对应的ASCII码值,用实线连接的点表示明文ASCII分布,用点连接的“*”表示使用明文"chaoticcryptosystemblockcipher”加密后密文ASCII分布,用虚线连接的“+"表示明文“ahaoticcry ptosystemblockcipher”加密后密文ASCII分布口比较图4的密文分布,可以看出两者完全不同,很明显对明文是敏感的。
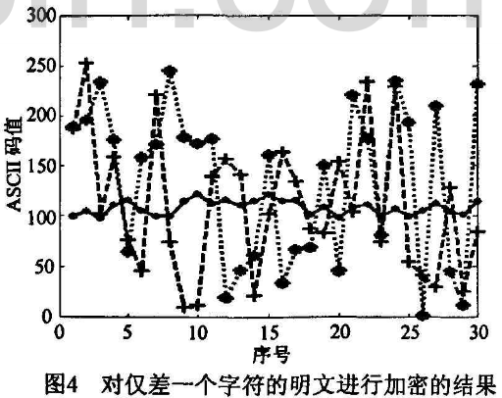
本文的算法表现出的对密钥和明文的敏感性和密码系统相吻合。
3、抵抗各种攻击分析
比较典型的穷举攻击方法有;唯密文攻击(ciphertext only attack)、已知明文攻击(knownplain text attack),选择明文攻击(chosen plaintext attack)、选择密文攻击(chosen ciphertext attack)。很显然如果密码系统能够抵抗选择明文攻击,则足以抵抗其他各种攻击。根据KerchofPs准则,假定密码分析者知晓除密钥以外的所有事情。在本文的算法中,通过输出反馈的方式,后面输出的密文都与前面加密的明文相关,密码分析者不可能得到与明文无关的密钥流。加上使用的3个混沌映射的系统参数、初值和迭代后的值均平均约有252个取值,迭代次数取值空间平均约为29,因此每一步迭代的密钥空间约为3×22xS2+9≈2115,密钥空间非常大。在目前的计算条件下,密码分析者通过选择一些明文和相应密文来穷举子密钥是非常困难的,而在算法中整个密钥空间为2128,通过密钥的扩散,其加密强度要远大于2128,要想恢复出整个密钥更是难上加难。
小知识之ASCII
ASCII是基于拉丁字母的一套电脑编码系统。它主要用于显示现代英语和其他西欧语言。它是现今最通用的单字节编码系统,并等同于国际标准ISO/IEC 646。










