针对混沌系统产生的混沌序列具有遍历性、伪随机性、对初始条件(值)和系统参数敏感以及具有类似白噪声等特点,提出了一种利用多个混沌系统结合的方法对彩色图像进行加密的算法,首先利用Arnold变换对图像进行像索置换,然后利用统一混沌系统对图像像素加密处理,在加密的过程中利用Logistic混沌系统对统一混沌系统序列进行乱序处理。
一、Arnold映射
众所周知,图像相邻像素之间有着非常强的相关性,大量的统计分析表明一幅图像相邻的水平,垂直或对角线的8到16个像素之间存在着强相关性。为减少这些像素之间的这种强相关性,我们采用了Arnold变换来置换图像像素的位置关系来降低像素之间的相关性。
假设原始图像I是大小为N×N,灰度级为256的灰度图,图像像素的坐标表示为C={(x,y)|x,y=O,1,2,….N-1},则Arnold变换可表述为:
![]()
其中p和q为正整数,x和y为原图像像素的位置。x’和y’为变换后图像像素新的位置。当对图像进行n次Arnold变换,即:
![]()
不断地改变图像像素之间的位置,使得原图变得混乱不堪。
若再进行若干次Arnold变换后,原图可能被还原,即Arnold变换具有一定的周期性。因此为了增强图像的加密效果,一般还需要与其他变换结合来使用。
二、统一混沌系统
其作为Lorenz系统、Lǖ系统和Chen系统之间的桥梁,因此统一混沌系统是更为一般意义上的混沌系统。该系统的数学表达式为:
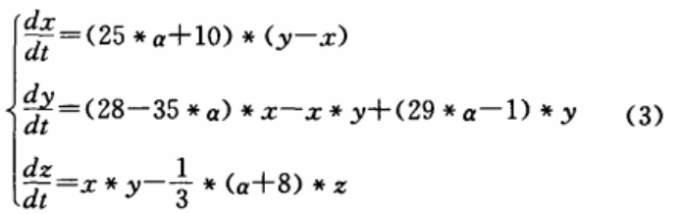
其中,x,y,z和α为实数,当α∈[O,1]时,系统处于混沌状态。
特别,当α=0时,式(3)是Lorenz系统,当α=1时,式(3)为Chen系统;当α∈[o,1]之间时,系统为统一混沌系统。因此统一混沌系统表现出更加复杂的动态行为。
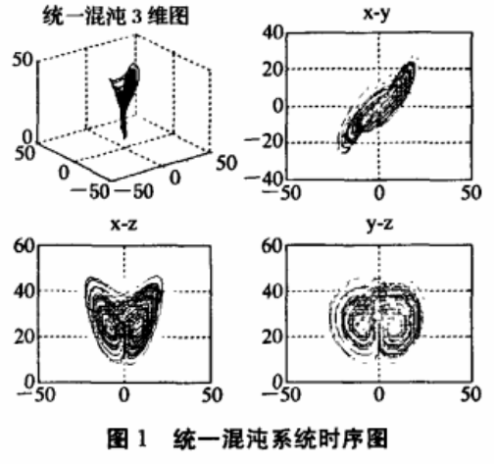
图1是当α=0.5,x=10,y=12和z=12时,统一混沌系统的时序图。
三、Logistlc混沌系统
Logistic是比较早被人们研究的一类混沌系统,其具有表达形式简单,易实现等优点被广泛使用在多种场合,其数学表达式为:
![]()
其中0≤μ≤4为分岔参数,xk∈(0.1),当3.5699456…<μ≤4.0000时,Logistic系统将表现为混沌性,此时产生的序列(xk,k=0,1, 2,3,…)为混沌序列。
图2是当x=0.6时,Logistic系统随μ的分岔图,从图中可以看出系统随μ的增加,系统将表现出非常复杂和丰富的动态行为,特别当μ=4时系统;进入到混沌系统。
图3是当μ=4、x=0.6时,Logistic混沌系统的时序图。
四、多混沌彩色图像加密算法
多彩色图像加密算法由3部分组成。首先利用Arnold变换对彩色图像的原始图像像素的位置进行置乱变换,接着将统一混沌系统产生混沌序列,并将其转为整数,然后利用Logistic混沌系统产生的序列改变上面的整数序列顺序,最后利用新的序列分别对彩色图像的各层按顺序依次进行加密改变相应层的像索灰度值。
1、Arnold对彩色图像置乱
利用Arnold变换分别对原始彩色图像的R,G,B层像素进行置乱,其中迭代次数可以视为密钥,为了减少运算,令p=1,q=1。
由于Arnold变换存在零点位置不变性,因此存在一定的安全隐患。为了克服零点位置不变性,首先对每一个图层的原图进行,n次Arnold变换,然后再对Arnold变换后的中间图进行水平(或垂直)镜像,接着进行撒次Arnold变换。这样零点位置也将被打乱,这样同时又对图像像素做了进一步的混淆。
2、加密序列的生成
加密序列的生成由下列3个步骤组成,具体如下:
步骤1 由式(3)的统一混沌系统在初始值{x1,y1,Z1}和设定好α值时使系统处于混沌状态,即{x1,y1,Z1}和α值作为初始密钥。再利用步长为0.001的4阶Runge-Kutta数值算法不断迭代计算获得3个混沌序列X,y,Z,它们分别为:

其中n为图像的大小,假设图像大小为n=MXN,{x1,y1,Z1}为初始值,X,y,Z分别由{x1,y1,Z1}不断迭代产生的集合。由于x1,y1,Z1都是实数集,不能直接用于图像加密,还需进一步处理,接着采用式(6)的方法对式(5)数集进行处理而获得介于0~255之间的整数。

其中int表示取整运算,mod表示取模运算,256为最大的图像像素灰度值决定。abs表示绝对值。由此,R,G和B构成了三个整数序列。
步骤2 由式(4)的Logistic混沌系统按式(7)的规则产生如下的一个整数序列。
![]()
其中Li=[ 4*4*xi* (1-xi)],以为图像的大小,xi为式(4)不断迭代产生的数,xi为Logistic混沌系统的初始值,可以作为密钥的一部分。符号[ l ]表示取不大于l的最大整数。由此可知,li∈u,U={0.1,2,3}。
步骤3利用式(7)产生的序列按式(8)规则对式(6)进行变换处理,
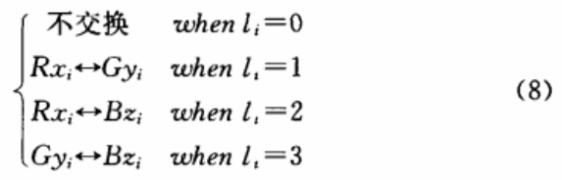
其中Rxi∈R,Gyi∈G和Bzi∈B,符号→表示该符号的前后两个数进行交换。
经过上述步骤后产生能够用于加密彩色图像的新序列。
3、彩色图像文件加密
利用式(8)产生的新序列分别对彩色图像的R、G和B层像素的灰度值分别按式(9)进行操作:

其中符号+表示异或操作,Rxi,Gyi和Bzi是由式(8)在第f次产生的整数对,IRi,IGi和IBi,分别为原始图像在第I个位置的R,G,B层像素灰度值,IRi',IGi'和IBi'为加密后彩色图像的像素值。
五、试验仿真结果
下面对512×512大小的彩色Lena图像采用前面所述算法进行仿真。
1、Arnold变换仿真
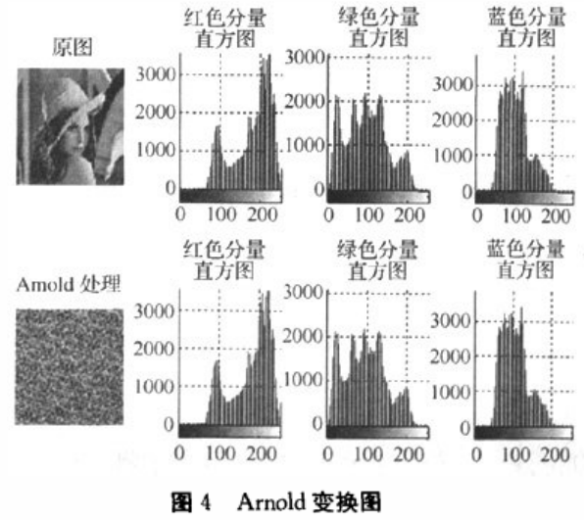
利用按照前面介绍的Arnold变换算法对彩色Lena进行置换处理,其中先镜像n=10次Arnold变换,接着进行网像水平镜像,最后镜像m=7次Arnold变换,仿真结果如图4所示。
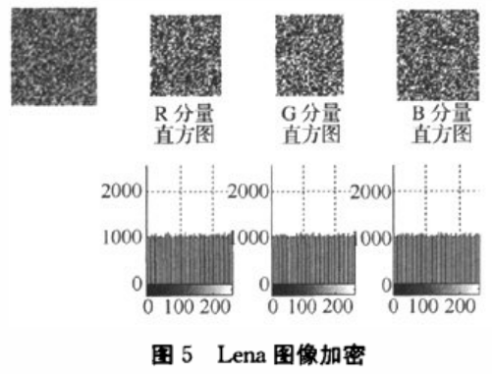
由如图4所示的直方图中可知Arnold只是将图像的像素打乱,其灰度值并没有发生变化。
2、加密序列的仿真
按照5.2节的方法,对统一混沌取x=1O,y=12,z=19和α=0.5作为初始值,代入式(3)并且不断迭代生成混沌序列X,y,Z,它们长度都为图像大小512X512。
假设Logistic混沌系统的初始密钥为l=O.123456789,按照前述算法将获得介于[0,3]之间的整数序列,其长度为图像大小512×512。
3、彩色图像加密仿真
对Arnold变换后的图像,并利用获得的加密序列进行加密处理。如图5所示,加密后图像的R,G,B各层图像变得无法阅读,并且对应的直方图也变得非常平坦和均匀,显然不同于原图的直方图,即表明加密后的图像的灰度值完全地被均匀分布到整个灰度区间,所以加密后的图像有着非常好的统计特性,从而能够抵抗统计攻击而使之变得无效。
下面测试彩色图像加密速度,其测试结果如表1所示。

表明所提出的加密算法在加密速度上快于DES的加密速度。
上述仿真是在个人计算机环境下进行测试的,其测试平台配置为:CPU: Pentium 4 2.6G;内存:512M;操作系统:Windows XP。基本测试图像为512×512大小的彩色Lena图像。
七、安全分析
下面对彩色图像加密算法的安全分析从下面几个方面来分析:相邻像素的相关性、抗差分攻击能力、一次一密、密钥的空间以及密钥敏感性等4方面,具体如下所述。
1、相邻像素的相关性分析
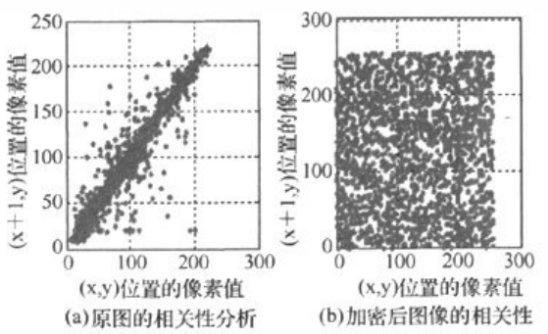
下面是原图与加密图相邻像素的相关性分析,分别随机地从原始和加密后的图像中取随即取1500个相邻像素对(水平,或垂直或对角线)。图6显示的是原网与加密后图像R层的水平相关分布图。从左图可以看出加密前的R层图像的相关性很强,右图2是加密的图,其相邻的像素完全均匀分布到了整个图像空间。
对彩色图像的B层和G层做了相同的测试,结果均与图6相同。
为了计算像素的相关性,可以使用下面公式:
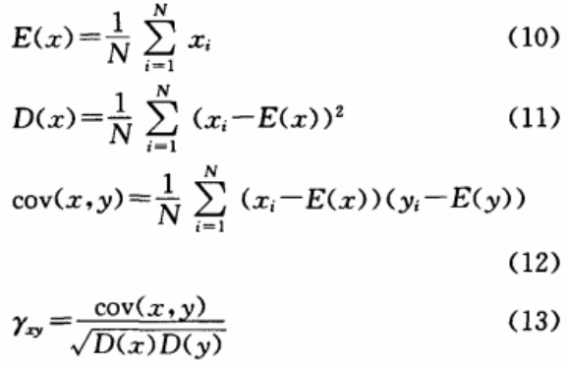
其中x和y是图像中相邻两个的灰度值。
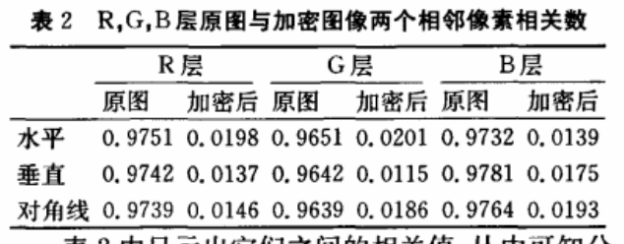
表2中显示出它们之问的相关值,从中可知分析出:原网中相邻两个像素值之间的相关性很强,而加密后图像相邻两像素之间的相关性却减少到很低了。
2、抗差分攻击能力分析
通常攻击者可以通过对图像作微小的改变来观察加密的效果,这样可能发现原始图像与加密图像之间的某种关系。但如果对原始图像进行微小的改变后导致加密图像有很大的改变,这样差分攻击方法将失去作用。
为分析抗差分的攻击能力,一般采用两个参数对这种变换进行描述,即像素变化率(NPCR)和平均变化强度(UCAl)。对于一幅原始图像经加密处理变为C1,如果对原始图像修改了一位像素的灰度值后再进行相同条件下的加密处理变为C2,比较灰度值矩阵C1和CZ所有点的值,如果两点相同,即Ci(i,j)=Cz(i,j),则D(i,j)=l,否则D(i,
j)=0。NPCR和UCAI具体定义为:
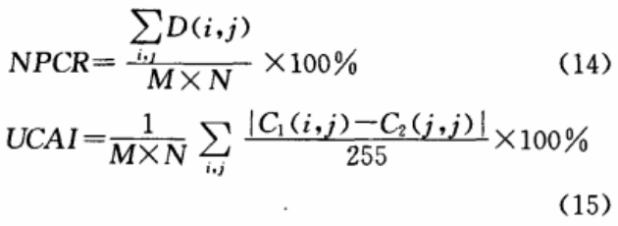
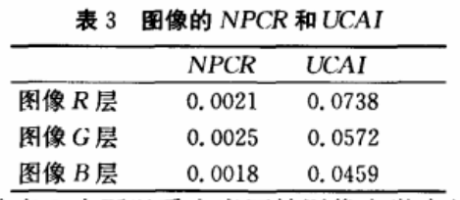
其中M和N分别为图像的长和宽。以彩色Lena图像的RGB作为测试对象,假设加密图像为C1,当修改了某一个像素的灰度值后的加密图像为C2。分别根据式(14)和(15)分别计算R,G,B层的NPCR和UCAI值,具体如表3所示。
从表3中可以看出当原始幽像有微小的改变而将导致加密图像有很大的改变,因此该算法具有良好的抗差分攻击能力。
3、一次一密分析
根据Shannon提出的一次一密加密的算法是安全的原则,由于混沌系统产生的混沌序列具有不重复性,而由多个混沌系统共同生成的序列将更加不会重复,因此多混沌彩色加密算法属于一次一密性的算法,由此可知该算法安全性是非常高的。
4、密钥空间分析
一个好的加密算法应该对密钥非常敏感,并且密钥空间要足够大以抵抗穷举攻击法。多混沌加密算法的加密密钥由各个混沌系统的密钥共同确定,因此该加密算法有着更大的密钥空间。假设计算机精度为1015,那么密钥空间将远远大于1075(=1015* 1015* 1015*1O15*1015)。因为统一混沌系统的x,Y和z。的取值范围不仅仅限制在(0.1)
之间,更可以为(0,1)之外的其他一些实数,只要xi,yi和Zi的取值不超过计算机的计算范围均可,并且还尚未计入Arnold的迭代此次作为密钥的情况,这么大的密钥空间足够抵抗各种穷举攻击。
5、密钥敏感性分析
由于混沌系统有着对初始值和参数及其敏感的天然性质,下面对其进行分析。
图7是当同定三个参数,而令另外一个参数发生微小变化(1015)的效果图和直方图。(加密密钥为x=10,y=12,z=19,l=0.12和α=0.5)。(说明:这里为了与统一混沌系统中的z区别.Logistic的初始值设为l,下同),设同定初始值x、y和Z不变,仅初始值z=19.00000000000001,即z有微小的变化进行解密,解密结果如图7所示,说明即使密钥有微小的差异也不能得到正确的图像。

类似的,当x,y和z不变,仅当初始值Z有微小变化l=0.120000000000001时对加密后的彩色图像进行解密,结果如图8所示,在这种情况也不能获得正确的原始图像。
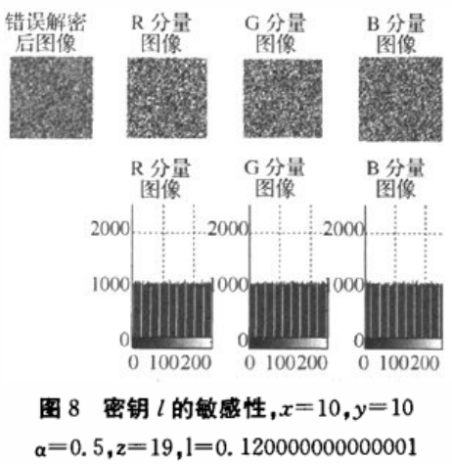
通过图7和图8所观察对应的直方图可以发现错误解密后彩色图像的直方图仍然保持均匀分布的特性,因此即使解密密钥有微小的变化也不可能正确解密出原始图像。
总而言之,该彩色图像加密算法具有以下优点:1)拥有非常大的密钥空间;2)加密后的图像有着非常好的统计特性;3)加密算法对密钥非常敏感。
小知识之遍历性
遍历性是指统计结果在时间和空间上的统一性,表现为时间均值等于空间均值。例如要得出一个城市A、B两座公园哪一个更受欢迎,有两种办法。第一种办法是在某一个时点考察两个公园的人数,人数多的为更受欢迎公园;第二种办法,随机选择一名市民,在一年的时间里考察他去两个公园的次数,去得多的为更受欢迎公园。如果这个两个结果始终一致,则表现为遍历性。









