针对低维混沌系统有可能退化为周期问题,以及高维混沌系统计算量大的缺陷,提出基于双混沌互扰系统的图像加密算法。通过两个简单的Logistic映射间的互扰,构造一个双混沌互扰系统。双混沌互扰系统的最大特点是扰动项同时包括常数扰动项和随机扰动项,不仅保证了系统必要的复杂性,而且增大了系统参数的取值范围。
一、双混沌系统互扰方案及混沌实值序列生成
在生态学中一些非常简单的确定性的数学模型却能产生看似随机的行为。如:
![]()
称之为人口方程,即著名的Logistic模型。其中xn∈(0,1),当控制参数3 569946--≤μ≤4时,Logistic映射表现出混沌的特性。
1、双混沌系统互扰方案
从两个简单的Logistic映射混沌系统模型出发,设计混沌系统互扰方案,迭代映射如下:

其中:mod为求余运算;x0、y0为混沌的初始值;cr1、cr2为常数,称之为常数扰动项;sr1(n+1)、sr2(n+1)为随机扰动项;μ1、μ2是混沌系统的控制参数。
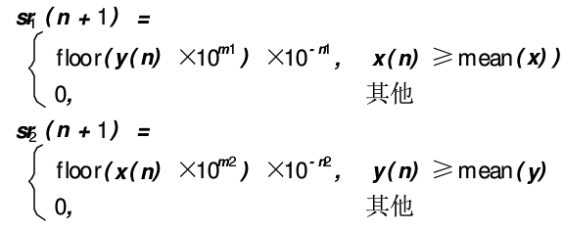
其中:floor是向下取整运算:mean是序列平均值:m1、n1、m2、n2为随机扰动项的控制参数。随机扰动项的随机性由混沌序列本身决定,即将混沌序列值与混沌序列的平均值相比较。
当系统参数cr1=e0.3,cr2=e0.4,m1=m2=2,n1=n2=8时,初值x0=0.1,y0=0.2。Logistic映射是在初始值x0∈(0,1),控制参数3,569946--≤μ≤4条件下才出现混沌现象,但在本文的双混沌互扰方案中,对初始值的取值范围没有任何限制,混沌系统互扰映射在控制参数μ1;1,μ2;2时各自都出现混沌现象,x,y∈(0,2),如图1的分岔图所示。
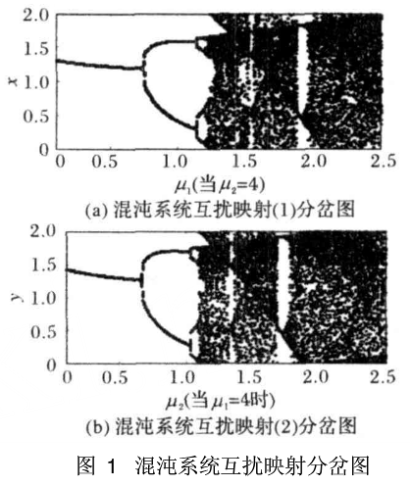
通过混沌系统间的扰动后,双混沌互扰系统变得更复杂,更加不可预测。与常用的超混沌系统和高维混沌系统相比较,本文构造的双混沌互扰系统具有以下优势:
1)构造混沌互扰系统时,可以任意选择相同或不同的多个混沌系统(不只限于两个混沌系统),构造方法灵活,且易于实现;
2)随机扰动项的随机性可以人为地控制,在不知道随机扰动项的随机性如何决定的情况下,对破译者来说亦增加了难度;
3)增加了系统参数的个数,扩展了初始条件的取值范围,进一步增大了密钥空间,安全性得到提高。
2、混沌实值序列的产生
由两个简单的Logistic映射混沌系统经过常数扰动和随机扰动后,得到两个混沌序列分别为:{x:x1,x2,x3,…,xn},{y:y1,y2,y3,…,yn},其中n为序列的长度。 定义1,用于产生二值序列的混沌序列z为:
![]()
式中j=1,2 3,…。
最终混沌序列提由Logistic映射互扰后得到的混度序{x:x1,x2,x3,…,xn},{y:y1,y2,y3,…,yn}交叉组合而成,为了消除初始值对混沌序列过渡部分的影响,选取迭代1000次后的序列值构成最终混沌序列z。
当参数为μ1=60,μ2=70,cr1=e0.3,cr2=e0.4,m1=m2=2,n1=n2=8时,初值x0=0.1,y0=0.2,系统参数不变,只是初始值x0或y0发生0.000001的微小变化,得到的混沌序列的差异相当明显。实验中选取了混沌序列的前40个序列值对比,如图2所示。
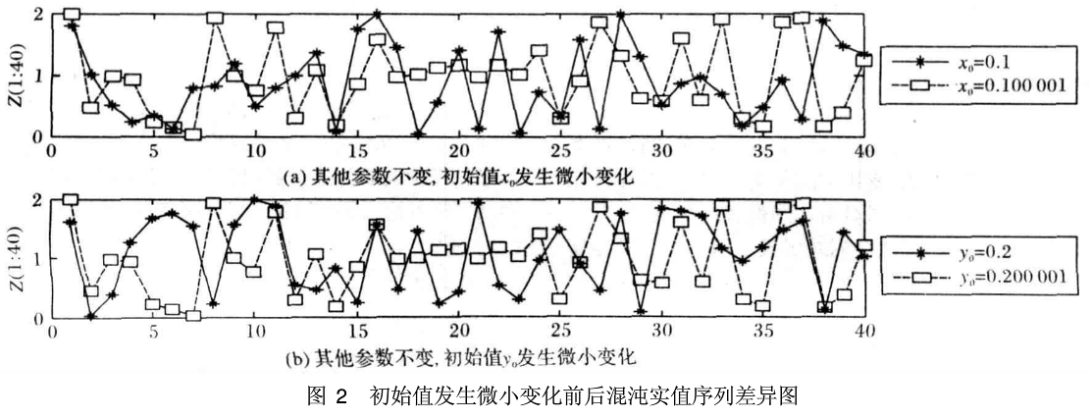
图2中,实线表示的是初始值未发生变化的混沌序列值,虚线表示的是初始值发生0.000001微小变化后的混沌序列值,实验结果也表明了由双混沌互扰系统产生的混沌序列对初始值具有十分的敏感性。
二、混沌二值序列的产生
由混沌实值序列转换为二进制序列的方法有多种。有将混沌序列值与混沌序列平均值进行大小比较,然后量化成0,1二值序列。有用混沌系统生成两个混沌序列,比较两个序列对应项的大小,然后量化成0,1二值序列。有基于一个四维混沌系统生成四个混沌序列,将混沌序列划分小区间,接着在小区间内取平均值后与0比较大小,然后量化成二值序列。 本文采取的二值量化算法如下:
1)设定双混沌互扰系统的初始值小粥,经过系统迭代映射产生混沌序列z;
2)提取混沌序列神每个混沌实值小数部分的2、4、6,组成一个新的3位整数,比如:0.372 685189—765,由这些整数组成新的整数序列I;
3)将整数序列对256求余预算,即I'= mod(I,256),比如765—253,这样就得到一个新的整数序列I',且序列I'每个值都在区间[0,255];
4)将得到的整数序列I'换成二进制序列{I':253→11111101},这样就完成了由混沌序列考z值序列s的转换; 所得到的整数序列,I'的直方图如图3所示。

可以看出,整数序列I'分布不够均匀,区间[225,255]的数明显偏少,这将影响图像加密效果。因此对量化算法进行改进,改进的量化算法如下:
1)设定双混沌互扰系统的初始值孙J6,经过系统迭代映射产生混沌序列z;
2)提取混沌序列神每个混沌实值小数部分的2、4、6位,组成一个新的3位整数,比如:0.372685189—765,由这些整数组成新的整数序列I1;提取混沌序列神每个混沌实值小数部分的3、5、7位,组成一个新的3整数,比如:0.372685189—281,由这些整数组成新的整数序列I2;
3)将整数序列I1、I2分别对256求余预算,即I1'=mod(I',256),比如765—253;,I'=mod(I2,256),比如281—25。这样就得到两个新的整数序列I1,I2且序列I1,I2的每 个值都在区间[0,255]内;
4)将得到的整数序列I1'、I2'的每个整数都转换成二进制,例如{I1':253—11111101},{I2':25—00011001}。分别提取二进制序列后面4位交叉排列,组成新的二进制序列S那么就有{S:1101 8 1001—11100011},以及与二值序列对应的整数序列I; 改进后得到的二值序列转换成整数序列I的直方图如图4所示。
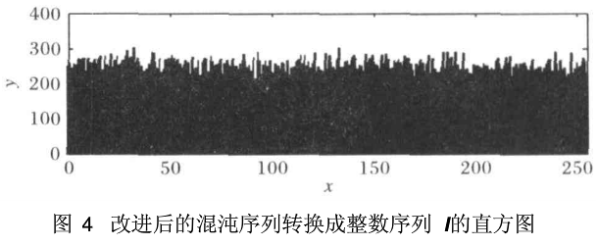
可以看出,改进后得到的整数序列I更加均匀。
三、加密流程及仿真试验
1、加密流程
1)设定双混沌互扰系统的参数及初始值x0,y0,经过系统迭代映射产生混沌序列z。
2)置换:由前面的方法对混沌序列量化得到混沌二值序列S同时将明文图像转换成二进制,然后从混沌序列S中每次取8个数与明文图像像素二进制值“异或”运算,最后转
换成十进制整数,这样就得到置换后的密文图像。
3)置乱混沌序列从小到大排列成Z',z'与z'排列前后之间的位置就形成了一组对应关系。将置换后的密文图像按照z'与z'的位置对应关系重排,得到最终密文图像。
解密就是加密的逆运算,只有正确的密钥才能得到正确的恢复图像。
2、仿真实验
根据上节的加密流程用Matlab进行图像加解密实验仿真。试验中选取标准的Lena图像作为待加密的明文图像,如图6(a)所示,其灰度直方图如图6(e)所示。
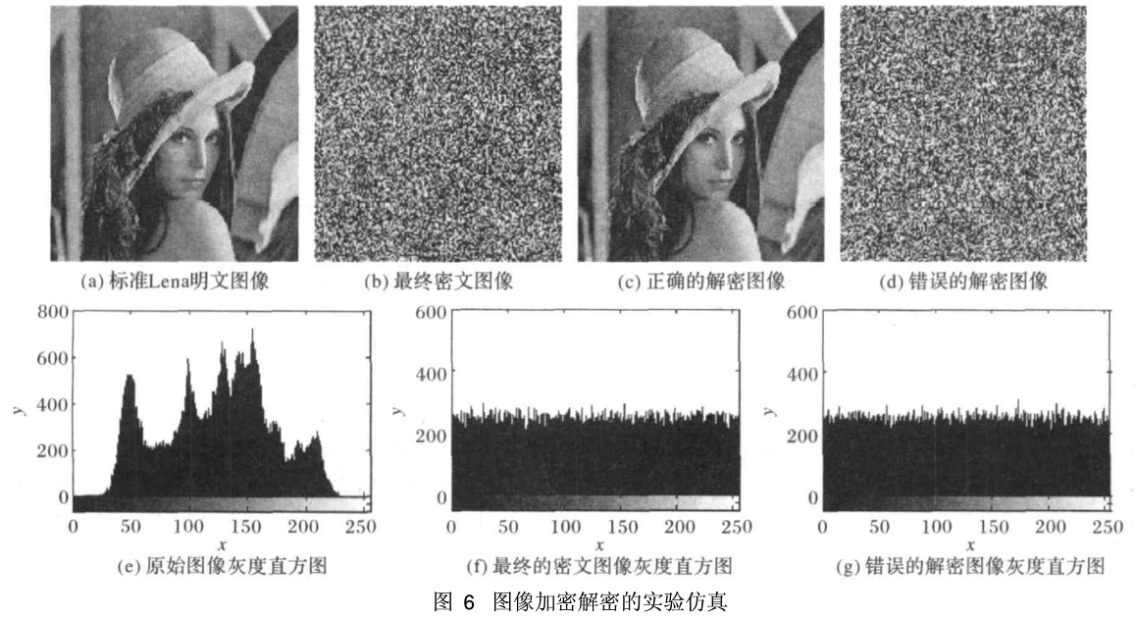
设定参数μ1=60,μ2=70,cr1=e0.3,cr2=e0.4,m1=m2=2,n1=n2=8时初始值x=0.1,y=0.2。按照的加密流程对明文图像加密,得到最终的密文图像如图6(b)所示,图6(f)是密文图像灰度直方图。通过原始图像与加密图像的灰度直方图对比可以看出,加密图像的像素灰度直方图非常均匀,说明二值序列能有效地掩盖明文信息。
小知识之MATLAB
MATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。











