混沌是指在确定性非线性系统中出现的类似随机的行为,一般认为,将不是由随机性外因引起的,而是由确定性方程直接得到的具有随机性的运动状态称为混沌。混沌系统的最大特点在于对初始条件十分敏感,从长期意义上讲系统的未来行为是不可预测的以及混沌系统的带宽非常宽。混沌系统的特征恰恰符合现代密码学随机的特征,将混沌应用于信息安全领域有着十分广泛的应用前景。
一、混沌理论在图像文件加密上的应用
基于混沌的图像文件加密方式,一是新近发展起来的一种新的图像加密算法。混沌图像加密方法是利用混沌信号来对图像数据流进行加密。混沌之所以适合于图像文件加密,这与它自身的一些动力学特点密切相关。因为混沌具有的遍历性、混合性和指数发散性等都非常适合于加密,它是一种天然的加密系统;混沌的不规则性,则为其在图像加密领域的应用创造了条件。图1为混沌序列加密解密原理图。
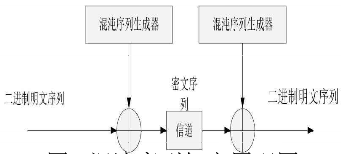
混沌序列密码体系的加密算法可以描述如下:
1)选定一个迭代初值x0。
2)i从1到L,完成下列步骤:
![]()
3)获得密文C=C1,C2…CL。
经过混沌迭代的调制之后,明文和密钥序列完全被融合在一起,作为同一个信息在信道上传输。混沌序列解密算法与加密算法相同,由密钥x0及得到的密文序列ci可以推出明文M。算法过程如下:
1)设定迭代初值x0。
2)i从1到L,完成下列步骤:
![]()
3)获得明文M=m1,m2…mL。
二、基于Logistic映射的双混沌多步图像文件加密
图像多步混沌置乱都是采用混沌像素值置乱与混沌像素位置置乱相结合的方法。混沌像素位置变换一般比较复杂,有多种方法。
本文采用了一种相对比较简单的方法如下:
1)选定两个混沌系统分别以初值x(0)产生两列混沌序列;
2)将序列归一化后分别乘以M和N;
3)将两列序列取整使得序列取值分别为[O,M-1]与[O,N-1]区间的整数;
4)对两个序列进一步处理得到遍历[o,M-1]的序列X![]() 与遍历[O,N-1]的序列
与遍历[O,N-1]的序列![]() ;
;
5)用这两个序列作为置乱矩阵的行地址和列地址,对原图像进行置乱。
1、Logistic混沌序列发生器模块
Logistic映射是一种重要的混沌模型。一般可用一个函数关系描述:
![]()
考虑最简单的模型:
![]()
讨论μ的值:
a)当O<μ≤1
此时该模型的状态简单,曲线迅速趋于O,且O就是吸引子,迭代方程最终归于O值不变。
b)当O<μ≤3
该模型状态比较简单,不动点O,1一1/μ为仅有的两个周期点。
c)当3<μ≤4
此时该模型状态十分复杂,系统由倍周期通向混沌。
d)当4<μ
此时该系统状态毫无混沌现象,O为唯一的吸引子。
由上述讨论可以看出Logistic系统随着μ增大的变化情况是:非混沌一混沌一非混沌,经过人们深入的研究,Logistic方程仅3.5669<μ≤4时,该方程呈现混沌状态,对于实际应用中,为了便于硬件的实现,通常令μ=4。
图2是Logistic混沌发生器模块,其仿真波形如图3所示。
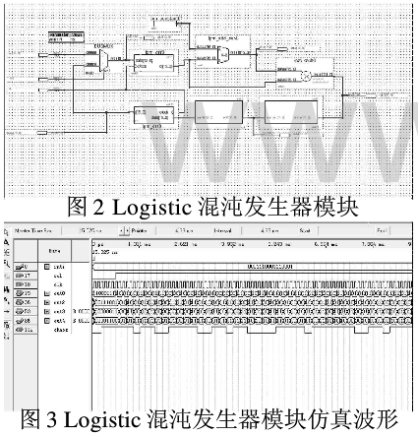
2、双混沌序列发生器
图4为双混沌序列发生器框图,是由两个Logistic发生器通过迭代组成的,Logisticl是一级混沌序列发生器,Logistic2是二级混沌序列发生器,它们的作用是根据初值产生相应的混沌序列。整个发生器有一个初始值x0。
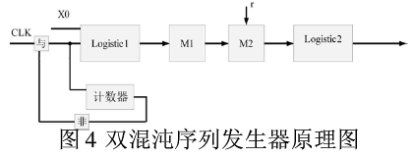
M1的作用是储存Logisticl发生器产生的初始混沌序列,将它们按产生顺序排列。
M2的作用为接收从M.传出的数值,取其值加上一个数值r作为Logistic2混沌发生器的初值。
计数器用来记录Logisticl产生混沌序列的个数,并通过一个与门来控制时钟CLK,当Logisticl产生的序列个数达到我们的要求,计数器就通过与门使时钟停止,这时Logisticl将不再继续产生序列。
系统有最少两个密码:x0和r,这样就增加了整个系统的安全性。
图5为图像文件的加密和解密图像,从图中可以看出,原始图像经过多次的迭代加密后已经完全看不出原图像的特征,图像反映的只是杂乱的不同像素值的像素点,在解密的过程中,如果输入错误的密码,解密后的图像仍然是杂乱的,只有输入正确的密码初值,才能够准确的解出原图像。

小知识之吸引子
吸引子是一个数学概念,描写运动的收敛类型,它存在于相平面。简言之,吸引子是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出发的非定常流的所有轨道都趋于它。这样的集合有很复杂的几何结构.由于吸引子与混沌现象密不可分,深入了解吸引子集合的性质,对更好了解它们所描述的流,对揭示出现混沌的规律与结构是很必要的。











