基于LZW压缩提出了一种安全的LZW( SecureLZW,SLZW)编码算法,SLZW编码算法利用动态增长的Huffman树作为字典,有效地将LZW和动态Huffman编码结合为一个整体,能显著提高压缩率。在编码的过程,利用基于混沌的耦合映像格子(Coupled Map Lattcie,CML)产生随机比特流控制Huffman树的编码,实现在压缩过程中进行加密,达到较好的安全性。
一、LZW编码和动态Huffman编码
SLZW编码的思想是建立在LZW编码和动态Huffman编码的基础上的,下而首先对这两种编码作简单介绍。
LZW编码的主题思想是用较短的字符串代替较长的字符串实现数据压缩,具体做法为:用一定的规则选择一些字符串放进字符串表(字典)中,当字典中的字符串再次出现时,就可以用字典中的位置索引值代替该字符串。LZW在解码时可以构建出同编码方同样的字典,因此,编码方构建的字典没有必要发送给解码方。
动态Huffman编码在对数据进行编码时不必事先统计数据出现的概率信息,它采用的是根据数据输入动态构建Huffman树的技术。更为重要的是,解码方在解码时不必事先拥有编码方构建出的Huffman树,解码方可以根据得到的压缩码流动态构建出与编码方一样的Huffrnan树,从而恢复出被编码的消息。这也是它和LZW编码结合起来后解码方能完全恢复出编码方字典的关键。
研究表明,将LZW与Huffman编码结合能取得更好的压缩效果,然而,这些方法均存在一个显著缺陷,就是没有将两个压缩过程无缝地合并为一个压缩过程,它们采用的思想都是在LZW压缩过程中计算出输出数据的概率,然后根据这些概率再对结果数据进行Huffman编码。本文将动态Huffman树结构作为LZW的字典,无需统计数据概率信息,一次LZW编码后即实现了总体压缩的效果。
二、SLZW算法
1、算法原理
SLZW编码和解码的原理如图1所示,它由两部分组成:一个经过改进的基于动态Huffman树的LZW编码器(或者解码器)和一个密钥流产生器(SLZW编码和解码过程采用相同的密钥流产生器)。编码过程为:明文M在密钥流譬的控制下,通过改进的LZW编码器,产生最终的密文C。解码过程为其逆过程。
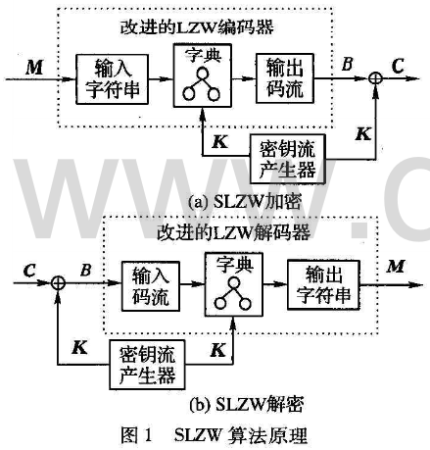
加密算法执行过程主要包含三个步骤:首先是产生密钥流,然后是基于动态Huffman树进行LZW编码,最后是异或产生密文输出。下面本文分别对这三个步骤进行详细的描述。解码过程为其逆过程。
2、密钥流的产生
密钥流产生分两步:首先,利用一个基于斜帐篷映射的二维CML混沌系统,CML的定义为:
![]()
其中xnj表示空间维为第j维(j=0,1),时间维为第n维(n=0,1,...)的变量,ε∈(O,1)。f(x)选择为斜帐篷混沌映射函数,其定义为:
![]()
其中a∈(0,1)。
然后,利用式(3)对产生的混沌变量进行二值化处理,生成二进制的密钥流K=kok1…kn。
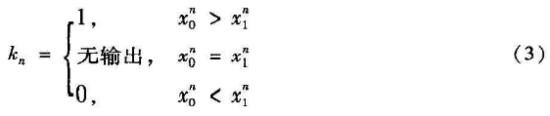
通过该方法产生的二进制随机序列能够克服混沌系统在数字化过程中的精度退化问题,具有较好的密码学特性。该密钥流用来对Huffman树的构建过程进行控制,以及与编码结果进行异或。
3、基于动态Huffman树的LZW压缩
在改进的LZW压缩算法中,我们将LZW中的字典采用动态Huffman树进行编码,根据字典中各词条出现的频率分配和调整其权值,从而达到提高LZW压缩效果的目的。
在编码的过程中,每当有新的符号(或者符号序列)加入到字典中或者字典中现有词条的频率改变时,就需要对这棵Huffman树进行更新。Huffman树中的节点包含LZW算法中的字典信息。在没有加入密钥的情况下,左子树的编码值为0,右子树的编码值为1。
构建初始字典的过程即为创建初始Huffman树的过程。将信源符号集中的每个符号(即LZW字典中的每个符号)赋初始权值1,然后按照Huffman树的构建规则建立初始化的Huffman树。在将每个符号加入到Huf:fman树的叶子节点的过程中,我们依次取出密钥流中的一位,若该位的值为1,则交换左右节点的编码值;否则不交换左右节点的编码值。
在利用Huffman树构建的字典进行LZW编码的过程中,每当一个符号(或者符号序列)被编码后,如果它在字典中已经存在,便更新其权值(将其权值加1),然后根据新的权值调整Huffman树的结构;如果该符号(或者符号序列)在字典中不存在,则初始化其权值为l,然后将其加入到Huffman树中。更新过程跟初始化Huffman树类似,由密钥流控制节点的编码值。
4、最终密文的生成
虽然本文在前面的步骤中已经通过密钥流混淆了初始化和LZW编码过程中产生的字典,为了掩盖密文的统计特性,进一步提高安全性,本文利用密钥流对产生的码字进行异或,产生最后的密文输出C= COC2...Cn...,即:
![]()
其中bn为改进的LZW编码器的输出。
三、实验结果与分析
为了验证所提出的SLZW算法的正确性和安全性,将其应用于GIF图像加密中,并且采用国际上通用的USC-SIPI图像测试库对算法进行了测试和验证(图片库中的图像默认是tiff格式,本文将其转换成gif格式后进行实验),实验结果表明SLZW算法在显著提高LZW算法压缩效率的同时达到了较好的安全性。但是由于篇幅限制,本文在此只以一幅大小为256 x256的Lena图像为例。
1、实验参数和加解密效果
产生密钥时需要设定一些初始参数,本实验中各参数值选取为:a=0.67899,ε=0.11228,x00=0.167862987,xo1=o.870612 439。其中xo0和xo1为二维CML的两个初始值,a、x00和xo1设定为算法的密钥。
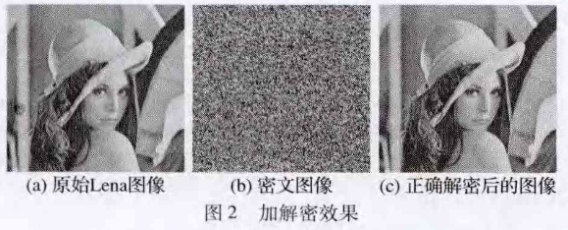
图2(a)是原始图像效果图,图2(b)为利用SLZW算法加密后的结果,图2(c)为正常解码后的固像。从图2(b)可以看出加密后的图片呈均匀噪声分布,不能分辨出任何关于
明文图像的有意义的信息。而图2(c)说明在给定正确密钥的情况下SLZW算法能够精确恢复出明文图像。
2、压缩效果分析
对于基于压缩的加密算法丽言,一个基本的要求是不能因为引入加密而给压缩效果带来负面的影响。对于上述的Lena图像,SLZW算法的压缩效果如表1所示。表1分别给
出了原始图像数据的大小、经过LZW和SLZW压缩后图像数据的大小囊通过计算得知,SLZW的压缩率比LZW提高了10.74t%,可以明显看出SLZW算法在压缩效果上优于原始的Lzw算法。

3、安全性分析
3.1 密钥空间分析
一个好的加密算法必须具有足够大的密钥空间来抵抗穷举法的攻击争本文中,a,x11和x12作为密钥,这三个值均是双精度浮点型。在计算机中,双精度浮点数采用IEEE754标准进行存储,这种标准下,浮点数的尾数值占52位,故本算法的密钥空间可以达到252x3= 2156,具有较大的密钥空间,可以抵挡穷举法的攻击。
3.2统计分析
统计分析是试图利用密文统计特性恢复出明文信息,为了能够抵挡攻击者采用统计手段破解编码信息,加密后的图像应具有均匀的直方图,并且密文图像相邻两像素的相关性也必须尽可能得低。本实验分别对明文和密文图像的直方图,及其相邻像素的相关性进行了测试。
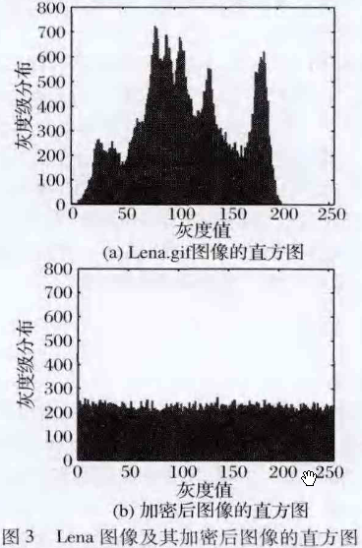
图3显示了明文图像和密文图像的直方图,通过对比,明文直方图的分布有多处峰值,而密文的直方图分布均匀,有效地掩盖了密文的统计信息,符合安全性要求。
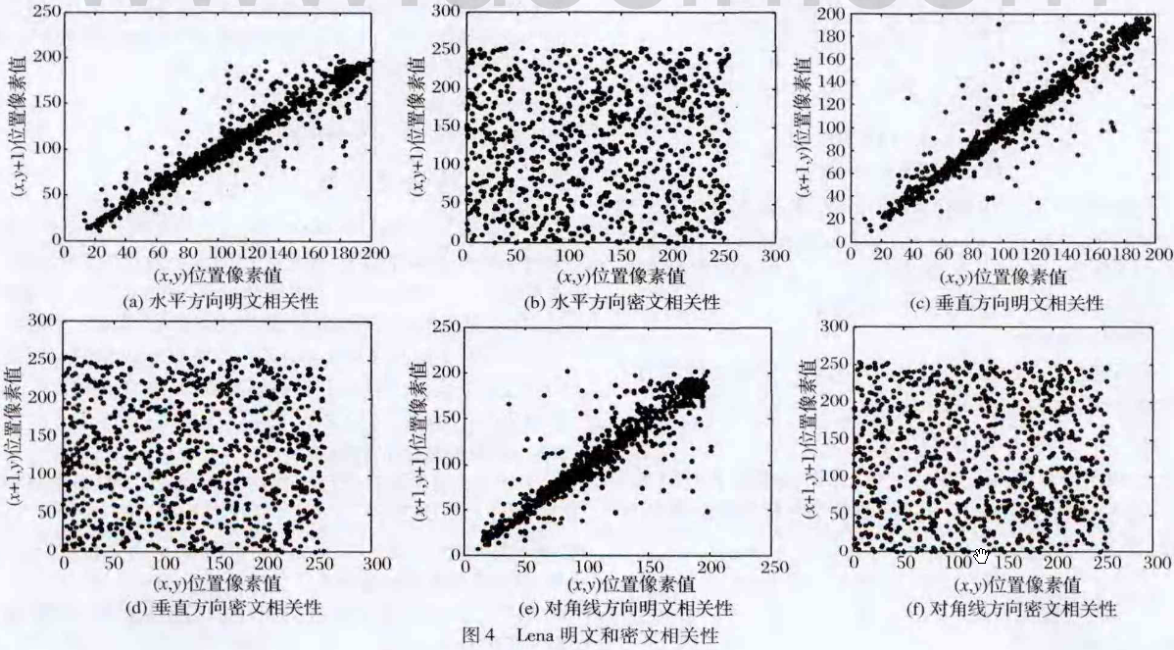
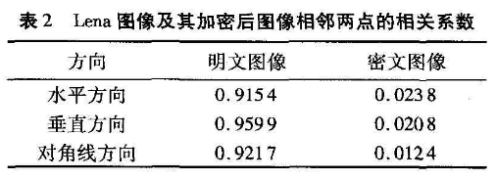
在相关性测试中,测试了水平、垂直和对角三个方向上两个相邻像素之间的相关性d对实验图像分别随机取出1000对像素点进行测试,结果见图4和表2。从图4(a),4(c)、4(e)和表2的笫2列可以看出,明文图像中相邻像素值皇楷状分布,其相关系数都在0.9以上,具有很高的相关性;而图4(b),4|(d),4(f)和表2的第3列表明,密文图像中相邻像素值的分布比较均匀,其相关性在0.02左右,从而表明密文图像中相邻像素的相关性已经非常小,满足安全性要求。
3.3敏感性分析
攻击者可能利用差分分析手段来获取明文图像和密文图像之间的相关信息,这就要求加密算法具有良好的密钥敏感性和明文敏感性。本实验测试了SLZW算法对密钥和明文的敏感性。
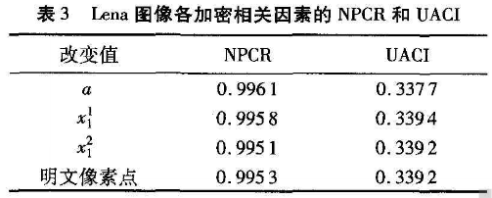
为了测试密钥敏感性,本文分别改变a,x11和x12值中的一位得到新的密文图像,然后求其与原密文图像之间的像素改变比率( Number of Pixels Change Rate,NPCR)和像素值的平均标准改变强度(Unified Average Change Intensity,UACI)。测试明文敏感性时,通过改变明文中的一个像素值来得到一幅新的密文图像,然后求共与原密文图像之间的NPCR和UACI。其中,a、x11和x12改变一位后的新值分别为0. 663 36,0. 167 924022和0.870 956 579,明文敏感性测试中改变的像素值坐标为(100,100)。
表3列出了密钥和明文敏感性实验的结果。观察可以看出:改变密钥或者明文的某一位,得到的NPCR均大于0.995,UACI在0.33左右,这表明算法具有良好的密钥敏感性和明文敏感性,能够抵抗差分攻击。
小知识之LZW编码算法
LZW就是通过建立一个字符串表,用较短的代码来表示较长的字符串来实现压缩。










