鉴于低维混沌加密存在密钥空间相对较小的局限性,基于三维蔡氏电路混沌系统的图像空域置乱加密方法可避免该局限性。利用产生的混沌序列,经过预处理生成置乱索引矩阵用于图像文件加密。该方案密钥敏感性高,可实现多幅图像文件的并行加密,是一种具有较高的安全性,加密效率高,且易于实现的图像文件加密。
一、Chua's Circuit混沌系统
近年来,许多学者通过非线性电路对混沌行为进行了广泛地研究,其中最典型的是Leon.o.Chua提出的蔡氏电路,它是能产生混沌行为的最小最简单的三阶自治电路。电路图如图1所示。
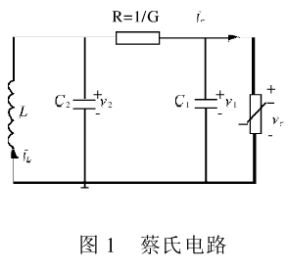
根据图l可以写出Chua's Circuit的三阶电路微分方程:

方程组(1)可写为如下的微分方程形式:
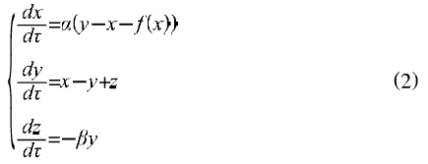
其中:
![]()
分析微分方程(3)的平衡点和Lyapunov指数,当参数α=10,β=15.68,a=-1.276 8,b=-0.6888时,蔡氏电路处于混沌状态,出现双涡卷混沌吸引子。
二、加密算法
1、伪随机序列的产生
首先利用蔡氏电路产生加密所需的伪随机序列。采用四阶Runge-Kutffi法迭代,控制参数设为(α,β,a,b)=(10,15.68,-1.27685,-0.688 85)积分步长h=0.0005,就可得到三维的混沌实数值序列(xi,yi,zi),i=1,2,…,n,n为数值积分算法的迭代次数。
对不同的控制参数产生的混沌序列(xi,yi,zi),的统计分析表明:3个分量(xi,yi,zi),;的值域分别为:xi∈(-4,4),yi∈(一1.8,1.8),zi∈(-20,20);对应的平均值分别为:avrx=-36.6,avry=-7.16,avrz=8.7226。再将此类序列用于加密前尚需做如下的预处理操作:
①去除各实数值的整数部分,统一值域;
②在去整的基础上再将小数点后移数位,以增强序列的无规则性及整体分布的均匀性。经过预处理后的伪随机序列(xi,yi,zi),i=1,2,…,n的值域为(10,-10),平均值分别为:avrx=0.00334,avry=-0.00950,avrz=-0.00152,趋于零。互相关特性近似为零,自相关特性是较理想的δ函数。
2、置乱索引矩阵的构建
利用上述的预处理后的序列,可构建一个如下的置乱索引矩阵I:
(1)矩阵I的定义:Iij∈{1,2,3,…}且Iij=Ipk当且仅当i=p,j=k。
(2)矩阵I的生成:将混沌系统产生的实值序列的各维经过去整、小数点移位等预处理后得到伪随机序列(xi,yi,zi),由3组伪随机序列生成矩阵X,Y,Z,对这3个矩阵的每一行向量进行排序。
控制参数的敏感性测试如表1所示,去掉序列的初始阶段,置乱矩阵的位序变化率可以达到100%。
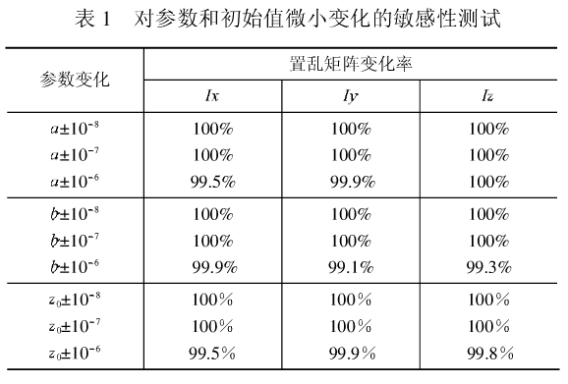
结果表明,预处理后的序列具有很强的伪随机特性,用于图像置乱将会获得安全性极高的加密算法。考虑到(xi,yi,zi)序列具有良好的各分量独立特性,利用xi,yi,zi这3个序列可独立的构成3个单变量加密混沌序列,也可组合构成多重加密序列,可同时对多幅图像进行加密,加密算法有良好的可扩展性。
3、加密解密算法
本文设计了一种利用置乱索引矩阵删图像进行空间置乱的加密方法。加密和解密算法如下。加密密钥可根据需要选择系统参数和初始值α,β,a,b,x,y,z中的一个或几个。加密步骤:
(1)输入原始图像。如考虑到图像压缩效果,则可以对图像进行分块预处理,以块为单位对图像进行全局置乱变换。为符合JPEG图像压缩标准,将图像分为8*8的块。这样做不影响DCT系数的分布。也可以直接对像素进行全局置乱,不需要预处理;
(2)构造置乱索引矩阵。输入密钥,生成实值混沌序列(xi,yi,zi),i=1,2,…,n,对3个分量进行预处理,按需要的长度截取实值混沌序列,为保证随机性,需去除序列的初始阶段。由混沌序列按规则构造索引矩阵Ix,Iy,Iz;
(3)图像置乱。按置乱索引矩阵的规则,重排置乱块的位置。为了获取更优的加密效果,对每幅待加密的图像选择Ix,Iy,Iz中的两个置乱索引矩阵构成二重加密,分别用于横向和纵向置乱。迭代2次即可达到理想的加密效果。如对8*8的分块进行置乱加密,迭代次数则应增加至3-5次。
解密算法为加密算法的逆过程:
①读入密图;
②重现置乱索引矩阵。
输入解密密钥,同加密步骤2;
⑨恢复原图像。是加密置乱过程的逆过程,根据置乱矩阵,将像素恢复到原位置。
三、安全分析和仿真测试
1、加密算法仿真
对上述加密算法进行了实验仿真,并对结果进行分析,验证算法的有效性和安全性。考虑到图像数据在网络传输过程中很难避免一些必要的数据处理或人为攻击,如压缩、噪声污染失真等。对这些常见的处理和攻击也进行了仿真测试。实验数据选择了具有不同纹理特征,大小为256a 256的lake,peppers,lena这3幅标准图像作为仿真对象。设置参数(α,β,a,b,x,y,z)=(10,15.68,-1.276 85,-0.688 85,1.584 102 3,1.234 585 4,1.895 278 1)利用蔡氏电路产生三维混沌序列(xi,yi,zi),对各维进行预处理并产生置乱矩阵Ix,Iy,Iz选择p2组合中的3种分别用于加密3幅标准图。图2为对lake图像进行的仿真结果,其中图2(a)为lake原始图像,图2(b)为加密后的图像,图2(c)为密钥误差为10-7时错误解密的图像。

图3为对peppers图像进行仿真的结果,其中图3(a)为peppers原图,图3(b)为加密后受到高斯噪声污染的图像,图3 (c)为用正确密钥解密后的图像。

图4为对lena图像进行仿真的结果,其中图4(a)为lena原图,图4(b)为对lena图像8*8的分块加密并进行有损压缩后的图像,压缩过程中保留了40%的DCT系数,图4(c)为正确密钥解密后的图像。

2、安全分析
通过对图2中加密前后的图像进行直方图、相邻像素相关分析以及差分攻击分析NPCR,UACI来验证算法的有效性。
2.1直方图分析
图5为lake图像加密前后的直方图显示。可以看出加密后的直方图中灰度分布的更均匀。
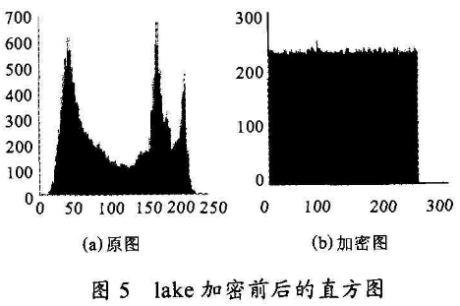
2.2相关性分析
图6为加密前后水平相邻像素的相关性分析。对随机产生1000对水平相邻的像素点,图6(a)为加密前的相关度。图6(b)为加密后同样位置的相邻像素的相关度。
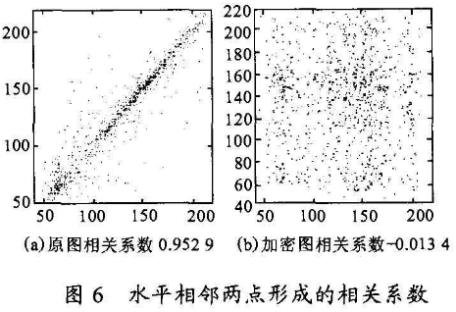
表2分别列出了加密前后相同位置的l000对水平相邻、垂直相邻、对角相邻的像素相关系数。加密前相邻像素相关紧密,加密后,其相关系数明显降低。相关系数的计算公式:
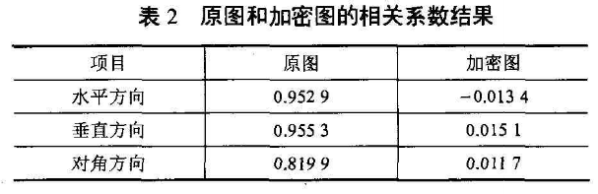
对图像加密前后的相关系数进行分析,可以看出,相邻像素间的相关系数大幅下降,可有效的抵抗基于统计分析的攻击。
小知识之蔡氏电路
蔡氏电路(英语:Chua's circuit),一种简单的非线性电子电路设计,它可以表现出标准的混沌理论行为。1983年,由蔡少棠教授发表,当时他正在日本早稻田大学担任访问学者。这个电路的制作容易程度使它成为了一个无处不在的现实世界的混沌系统的例子,导致一些人声明它是一个“混沌系统的典范”。











