admin 基于傅里叶计算全息技术，结合菲涅尔双随机相位加密系统，我们提出了一种数字图像文件加密方法。该方法以傅里叶计算全息图记录菲涅尔衍射双随机相位加密图像，傅里叶计算全息加密图像隐藏了原图像大小尺度信息，而且再现多个图像，必须针时加密图像共轭方可解密，提高了图像加密的安全性，并且解决了普通方法加密图像难存储的问题，作为原始明文的拥有者，两个随机相位板，应用波长，两次菲涅尔衍射的距离都可作为解密密钥。
一、图像文件的加密理论和计算方法
1、图像文件加密的理论模型
图像文件加密的理论光路图（如图1所示）是一个菲涅尔衍射双随机相位加密光路和一次傅里叶变换光路。
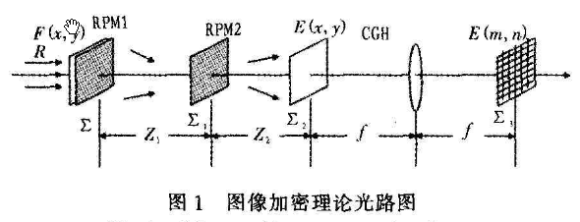
原始数字图像F(x，y)是一个复数矩阵，将其置于加密光路输入屏幕∑，引入单位振幅的垂直入射光R照射，并放置第一个随机相位板RPM1紧贴输入平面，出射光波首先受到RPM2的调制加密，然后经过一次距离为五的菲涅尔衍射到达第一菲涅尔衍射平面∑1，在该平面受到第二个随机相位板RPM2的调制加密，再进行一次距离为磊的菲涅尔衍射到达输出平面∑2完成加密。但是该加密图像为一复值矩阵，难以存储、传输以及保存，本文应用比较成熟的傅里叶计算全息记录加密图像，对该加密图像的频谱进行编码，将该复值矩阵转化为一实值的计算全息图，并且该图像为一幅隐藏了原图像大小尺度信息的全息图E(m，n)，在传输过程中更具有一般性，增加了图像传输的安全性。
2、图像文件的解密过程
根据光路的可逆性，解密过程为加密的逆过程，图像文件解密的光路图如图2所示。
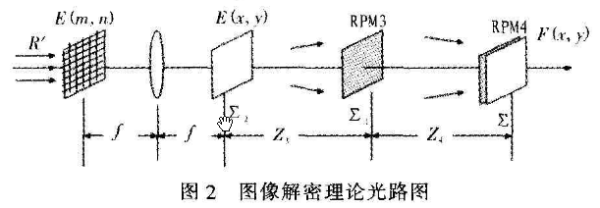
解密过程中，将计算全息加密图像E(m，n)置于输入平面，引入单位振幅的垂直入射光R’照射计算全息加密图，经过一次傅里叶变换，再现得到原加密图像及其共轭，由于菲涅尔双随机相位加密系统的特性，将计算全息加密图像再现的原加密图像共轭引入菲涅尔双随机解密系统，分别经过z3=z2，z4=z1的两次菲涅尔衍射以及两个随机相位板RPM3=RPM2，RPM4=RPM1的调制解密，在输出平面∑得到原始图像。
3、傅里叶计算全息加密图像的设计制作
本文采用罗曼Ⅲ型编码方法网，分别对加密图像频谱的振幅、相位进行编码，输出光场分布E(m，n)为复数，记为E(m，n)=Amn+jBmn，则相应的振幅为
，相位为φmn=arctan(-Amn/Bmn)。计算全息图编码的一个离散抽样点（如图3）所示。
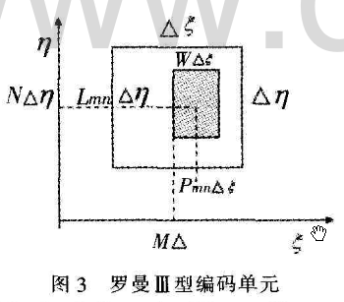
整个CGH共有M×N个抽样单元，图3为其中一个抽样单元。其中(m，n)为该单元的横纵坐标；△ζ、△η为抽样单元边长赶深色部分为通光孔径，面积Lmn△ζ×W△η编码该单元通光强度，反映频谱振幅信息，．罗曼Ⅲ型编码方式中，形不变，使Lmn与振幅成正比；由不规则光栅对相位调制原理，通光孔径中心与该抽样点中心的距离Prm与该点相对相位成正比，以达到用己。编码振幅和用Prr编码相位。
在计算全息的编码过程中，在对输出图像的频谱振幅编码时，对幅值A作归一化处理，以保证全息图中各抽样单元中的通光矩形孔高度不超过记录单元高度i在对频谱相位进行编码时，当φ>丌／2时，在程序中采用“模式溢出校正法”，以防止与邻近的矩形孔发生重迭而造成计算全息图再现时产生失真；在实现图像加密解密以及计算全息制作过程中，在编码前用Matlab中的移频函数fftshift()将频谱的高频部分移到靠近中心的部分。以完成计算机中正确的傅里叶变换。制得到计算全息加密图像如图4(c)所示，图4(a)为待加密图像，通过对比两图可见，计算全息加密图是一幅隐藏了原图像尺度大小信息的白噪声的图像，传输中更具有一般性，提高了图像加密及传输的安全性。
二、图像文件加密和解密的实验设计与分析
为了检验该数字图像文件加密方法的实用性，文中利用Matlab7.1对该方法进行了计算机实验。计算机实验的过程涉及离散傅里叶变换和相位板“调制”效果。用计算机中Matlab的离散傅里叶变换函数和计算机生成的随机矩阵与光场复振幅分布的点乘积模拟相位板“调制”。根据傅里叶计算全息再现共轭像的特性，针对该共轭像对该图像加密方法的有效性进行了检验。
1、傅里叶计算全息记录加密图像
用罗曼Ⅲ型编码方法，对菲涅尔衍射双随机相位加密图像(如图4(a)所示）的频谱编码，制作傅里叶计算全息图(如图4(c)所示）。
图4(a)为待加密图像“熊猫”，图4(b)为菲涅尔衍射双随机相位加密图像。是一幅随时间统计无关的白噪声图像，图4(c)是傅里叶计算全息加密图像，是一幅隐藏了原图像尺度大小信息的图像，在传输过程中更具有一般性。
2、傅里叶计算全息加密图像的再现
傅里叶计算全息图记录原加密图像的频谱，所以再现过程中，以垂直入射光照射计算全息图，出射光场经过一次透镜的傅里叶变换，再现图像（如图5所示）。
傅里叶计算全息再现图像特性，图中+1级单元为原加密图像，-1级单元为原加密图像的共轭，菲涅尔衍射双随机相位加密系统的特性，需要原加密图像的共轭作为解密图像，所以本文利用傅里叶全息的再现图像特性，将该单元引入解密光路解密。
3、图像解密密钥实验
利用图2图像解密理论光路，将图5中-1级傅里叶计算全息再现单元引入解密光路，对图像加密的各个密钥进行了解密实验，加密过程中，作为解密密钥的各参数：P1、P2为随机相位板，λ=0.63μm，z1=z2=0.3m，解密结果图像如F，图6(a)是正确密钥解密图像，即z4=Z3=z1=z2=0.3解密结果图像；图6(b)是Z3为错误密钥，选取Z3=0.305解密结果图像；图6(c)是Z4为错误密钥，选取Z3=0.301解密结果图像；图6(d)是P3为错误密钥，即P3+P2解密结果图像；图6(e)是P为错误密钥，即P4≠P2解密结果图像；图6(f)是解密波长λ=0.631l上m时解密结果图像；图6(g)是针对整个计算全息图再现像解密结果图像。
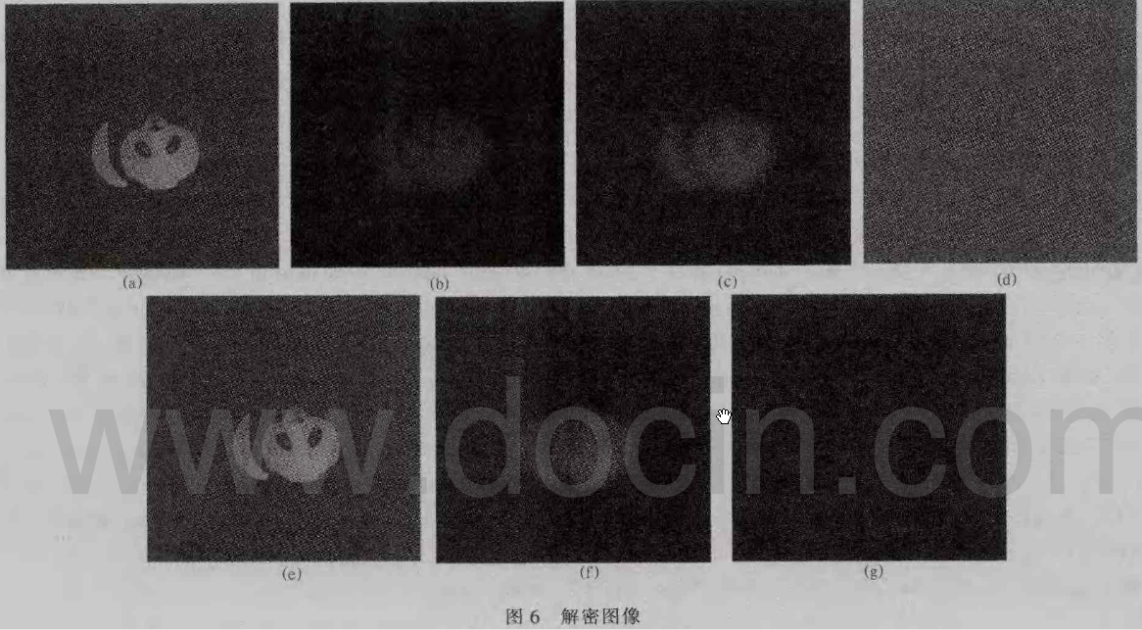
通过图6可见，各解密密钥正确时能很好地解密获得原图像，衍射距离Z1、Z2，相位板P2，应用波长都可作为解密密钥，而且相对Z1、Z2精度要求更高，由于所取解密图像光强图，P1不可作为解密密钥，同时计算全息图再现多个图像单元，增加了不知解密密钥时的解密难度。
小知识之菲涅尔衍射
菲涅尔衍射，或称菲涅尔衍射、近场衍射。是指在光源和障碍物间距离为有限远的情况下发生的衍射。菲涅尔衍射可由小孔、狭缝等产生。利用菲涅尔半波带法可以分析由衍射所产生的图案。
