基于全息理论以及随机位相编码的思想,我们提出了一种新的数字图像文件加密解密系统,该系统基于全息原理以及随机位相编码的思想,加密过程是通过全息记录原理以及随机位相编码方法在光学系统中实现的,解密过程借助于计算机,采用逆菲涅尔变换算法恢复出原图像。
一、加密光学系统
图1(a)所示即为本方法采用的第一种加密光学系统图。图中BS1和BS2是两个分光镜,M1和M2都为反射平面镜,SLMI、SLM2和SLM3分别为3个空间光调制器。其中,
SLM1为振幅型空间光调制器,SLM2和SLM3都为相位型空间光调制器。激光器发出的光经扩束镜扩束,成为准平面波。经扩束后的准平面波经分光镜BS1分为两路,一路经过SLM1和BS2进入图像探测器,另一路经M1、SLM2、M2和SLM3,并最终经BS2反射进入图像探测器。
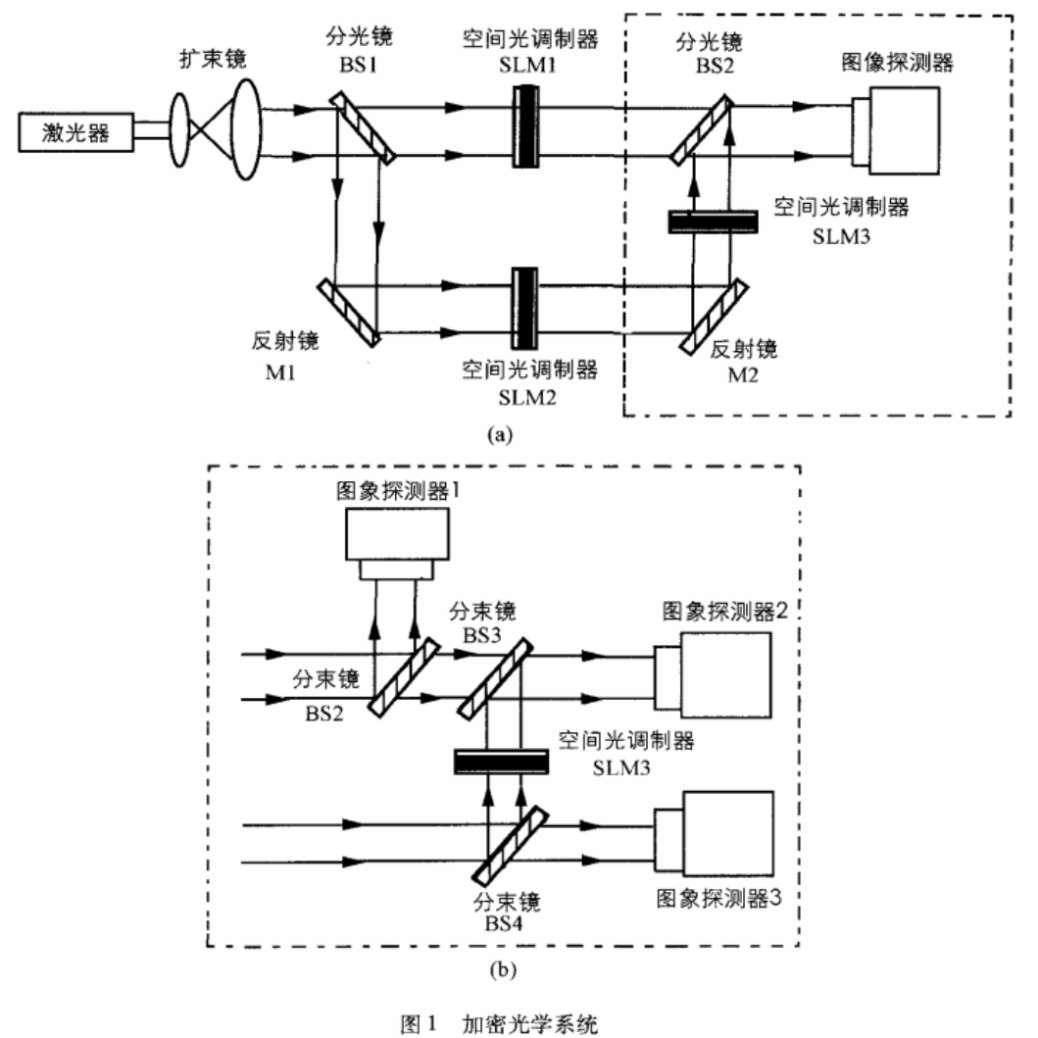
SLM1是一个振幅调制型的器件,把要加密的图像转换为透过率信息输入SLM1,于是第一路光便是携带了图像信息的物光波。第二路光经过SLM2和SLM3,其中SLM2是位相调制器件,把加密密钥信息(可以是随机位相)输入SLM2,这样第二路光就成为了被调制过的参考光;为了更准确地解密图像,我们利用了两次记录全息图的方法,系统中的SLM3作为位相延迟片使用,其中第一次记录时SLM3产生零(或2n整数倍)位相延迟,第二次记录时SLM3产生丌/2位相延迟o这里SLM3也可以由其他可交替改变位相的位相延迟片替代。
另外,要正确解密图像,需要知道4组数据:物光波的幅、参考光波的振幅、第一次记录的物光波和参考光波的干涉图以及第二次记录的物光波和参考光波的干涉图。
如果采用图1(b)的记录方式,图像探测器需要分别记录4次,这样会降低加密速度。为此,可以采用图l(b)的虚线框内的光路图来替代图1(a)中虚线框内的光路图;替代完后,物光波的振幅、参考光波的振幅和第一次记录的干涉图就可以一次得到。再调制SLM3使其产生rr/2位相延迟之后,第二次记录的干涉图也可以得到。这样,就省去了一半的加密时间。当然,如果再增加光路的结构,采用4个图像探测器,就可以一次得到全部4组数据(原理和图1(b)类似)。
二、加密方法描述
1、加密过程
设经扩束镜扩束后的光束都为位相相同(假设为Φo)、振幅为1的平面波。在第一路光路中,当该平面波通过SLM1时,被SLMl的透过率调制信息t(x1,y1)(该信息即为要加密的图像信息),从而其复振幅变为:
![]()
该光波即为物光波。
第二路平面波经过SLM2时被进行了相位调制,该相位调制信息即为一种密钥(设其为Φ(x2,y2),一般为随机相位分布),此时的光波为参考光波:
![]()
物光波和参考光波最终都到达图像探测器感光面上,这种光波在空间的传播是菲涅尔衍射,假设激光的波长为λ,SLM1后表面距离图像探测器感光面的距离为L1,则物光波空间传播到图像探测器感光面上的复振幅变为:
![]()
此处,G(x’,y’;x1,y1,L1,λA)为菲涅尔衍射积分核,表示为:
![]()
式(3)实际上是波函数O(x,y)的菲涅尔变换,可以简写为:
![]()
处,FrT代表对应波长为λ,距离为L1的菲涅尔变换。
同理,SLM2后表面距离图像探测器感光面的距离为L2,参考光波空间传播到图像探测器感光面上的复振幅可以表示为:
![]()
式中‘*’号代表复共轭。
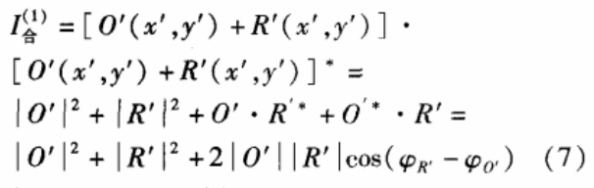
到此为止完成了加密的过程。
2、解密过程
解密过程正好相反,是要从记录的图案中恢复出被加密的图像信息t(x1,Y1)。
在式(7)中,物光波振幅|0’(x’,y’)|和参考光波振幅|R'(x’,y’)|都可以用图像探测器记录得到,而参考光波位相φR’(x’,y')在已知SLM2上的位相分布情况下可以由式(2)和式(6)算出。那么物光波位相分布φ0’(x’,y’)可否准确得出?答案是否定的。因为要得出φ0’(x’,y’)就要用到反余弦函数,而反余弦函数的值域为[O,π],不能满足位相在[O,2π]范围内的准确还原。因此,还需要第二次记录来得到更多信息。
假设在第一次记录时SLM3也在光路中,只要其位相延迟为2π的整数倍,以上分析仍然成立。当第二次记录时,让SLM3产生π/2的位相延迟,这样得到的第二次记录的干涉光场的强度为:
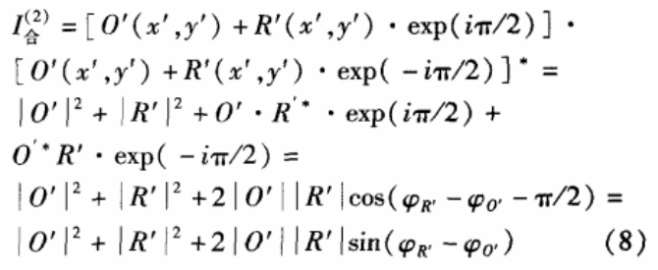
如前面所述,利用式(7)可以解出cos(φR’-φ0’)值。同理,利用式(8)可以解出cos(φR’-φ0’)值。由这两个值可以使用各种编程语言中的取两个变数的反正切函数(arctan2)来得到值域为[-π,π]的φR’-φ0’解,由此即可准确恢复出φ0’(x’,y’)信息。再由反菲涅尔变换可得到:
![]()
求O(x1,Y1)的模可得到被加密的图像信息:
![]()
在上述加密解密方法中,密钥信息被加载到参考光波上。也可以把密钥信息加载于物光波中(加密方案二),此时可以把SLM2放置在在SLMI后一定距离处(假定SLM1与SLM2之间距离为L11;而SI。M2与图像探测器感光面的距离为L12)。这样在计算时,物光波O(x1,Y1)就要经两次菲涅尔变换才可以得到O'(x',Y')即:
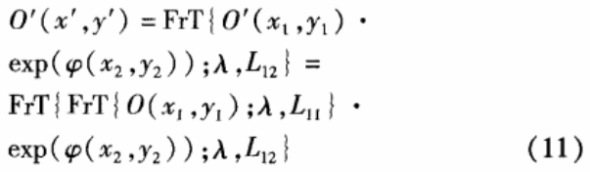
同理,解密时也要相应地进行两次逆菲涅尔变换才能得到O(x1,Y1),需要注意的是,这里的两个距离L11和L12也是一组密钥,不正确的距离恢复出的是错误图像信息。
三、结果及分析
1、方案一仿真结果
为了验证上述方案一,我们假设各参数如下:λ=0. 6328μm,L1 =40cm,L2=40cm,被加密图像尺寸为5mm x5mm,像素数为500×500;SLM2中的密钥也为尺寸5mm x5mm、像素为500 x500而位相随机分布在[O,2π]内的位相板。我们采用图2(a)所示的图像作为被加密图像,根据上述加密方法得到第一次记录时的干涉图如图2(b)所示。可以看到,从直接得到的干涉图中难以看到被加密图像的信息,必须经过解密程序才能恢复出原图像。利用上述解密程序并采用正确的密钥信息(包括SLM2中的位相分布,L1和L2)可以恢复出如图2(c)所示图像。

2、方案二仿真结果
下面来看方案二的加密效果。我们采用如下参数:λ=0. 6328ym,L11 =40cm,L12 =40cm,被加密图像尺寸为5mm x5mm,像素数为500×500为了要求大部分被SLM1调制的光信息能到达图像传感器可以看到该图像与原图像非常接近。为了验证该加密方法的保密度,我们采用错误的密钥信息( SLM2中的位相分布设为均匀分布)来恢复图像,采用上述解密程序计算得到所恢复的图像如图2(d)所示,该图像已经严重脱离原图像的面貌。
感光面,经试验,SLM2的密钥选用有序相位分布而不是随机相位分布,且尺寸为12mm×12mm,像素数仍为500×500。仍然采用方案一中的图像作为被加密图像(如图3(a)所示);SLM2中的密钥采用有序相位分布,其相位分布如图3(b)所示,图中的灰度值对应相位在[O,2π]内的变化。在图像传感器感光面上得到参考光和物光的干涉图如图3(c)所示,可以看到,仅从干涉图上看不到被加密原图的信息,必须使用密钥进行解密计算来恢复原图。使用正确的密钥L11,L12,以及SLM2中的密钥分布φ(x2,y2),采用解密程序可以计算得出图3(d)所示,该图像与原图近乎一致,说明该解密方法可行。
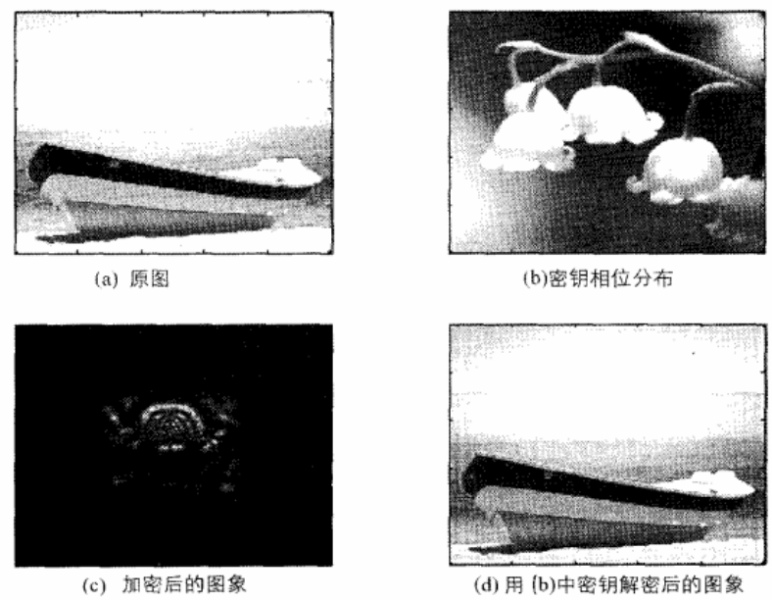
如果采用不正确的密钥进行解密,将不能得到正确原图像。现假设SLM2的位相分布不采用图3(b)中的值,而采用均匀位相分布。经解密计算,解密后的图像如图4(a)所示,可以看到此图严重丢失原图的信息。
小知识之全息原理
全息技术是利用干涉和衍射原理记录并再现物体真实的三维图像的记录和再现的技术。是利用干涉原理记录物体光波信息,此即拍摄过程:被摄物体在激光辐照下形成漫射式的物光束;另一部分激光作为参考光束射到全息底片上,和物光束叠加产生干涉,把物体光波上各点的位相和振幅转换成在空间上变化的强度,从而利用干涉条纹间的反差和间隔将物体光波的全部信息记录下来。记录着干涉条纹的底片经过显影、定影等处理程序后,便成为一张全息图,或称全息照片。











