对经典的二维Henon映射的混沌和密码学特性进行了详细的分析,并与传统密码学中广泛使用的Feistel结构进行了比较研究.在此基础上,提出一种新的不平衡的Feistel结构,并设计出一种基于该结构和Henon映射的混沌加密算法。
一、Feistel结构
在传统的对称密码学中,许多分组密码都采用了一种叫做Feistel的结构,如DES、RC5、FEAL、GOST、LOKI等。Feistel结构把任何函数都转化为一种转换,是一种典型的迭代结构,也是一种乘积形式的密码变换.它能够充分实现扩散与混乱,构成强度很高的密码系统。用数学式来表达,其第i轮的加密变换为:
![]()
其中,+表示按位异或,F是轮函数,Ki是第i轮的子密钥,式(1)所描述的是左右长度相同的“平衡Feistel结构”,在加密时,算法将长度为2n比特的明文分组m分为2个长为n比特的部分Lo和R,即nz=Lo Ro,每轮只对Ro进行加密,如DES就是采用的这种结构,考虑加密过程中的扩展置换,DES中需同时处理的长度是48 bit。采用的是左右长度不同的“非平衡Feistel结构”,分组长度同样为64 bit,但需同时处理的长度却是64 bit.大家知道明文分组长度越大,敌手破译的难度也越大,但计算机能够处理的字的长度却是有限的,又迫使分组的长度不能太长,可见,Feistel结构是影响分组密码算法中分组长度的一个重要因素,制约着分组密码算法的安全性和运行速度,因此,在实践中总是通过仔细设计Feistel结构,使同时处理的字的长度较小,而分组长度却较大。笔者这里设计出一种不平衡的Feistel结构,实现对较大的明文分组进行加密。
二、混沌系统及其特性分析
人类对混沌现象的认识,是非线性科学最重要的成就之一.经过比较深入的研究,人们发现一个混沌动力学系统的演化具有对初值高度敏感性、伪随机的轨道具有不可预测性、在信息传输过程中呈现连续宽带功率谱的特点.这些特性与密码学中对轮函数、伪随机序列发生器、长周期密钥等的要求非常近似,也正是由于二者有如此多的相似之处,近十年来,混沌动力学系统在通信、密码学中的应用才引起了人们广泛的注意,已发展成为一个非常活跃的研究领域。
将混沌理论中非常经典的Henon映射作为加密变换的轮函数,主要是基于2个方面的原因:一是理论上对其混沌行为的研究比较深入,二是它具有很好的密码学特性一 。
1、混沌特性
在非线性研究领域,对Henon映射的混沌特性的研究比较深入,对Henon映射:
![]()
它是一个二维的非线性混沌系统,具有很多优良特性。
2、密码学特性
Henon映射在保密通信、混沌密码中的应用比较多,但这些应用只利用了其混沌特性,而忽略了其特别优秀的密码学结构特性。
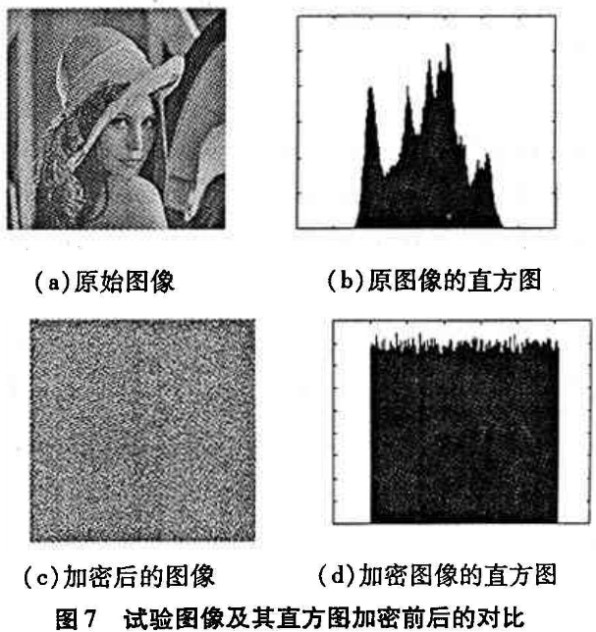
1)Henon映射作为密码算法中的轮函数,能够将其对初值的敏感性充分体现在加密算法对明文和密钥的扩散性与混乱性上,只要算法在初值或明文上有很小的改动,所得到的密文就“面目全非”。图1为初值分别取xo=0.234 5、yo =0. 123 4和xo =0. 234 6、yo=0. 123 5时迭代100次的x轨道图,图2为将图像“Lna”(见图7(a))运用笔者所设计的算法加密后的密文与将其第1O,1)个像素值从255改变为20时加密后不同的密文。
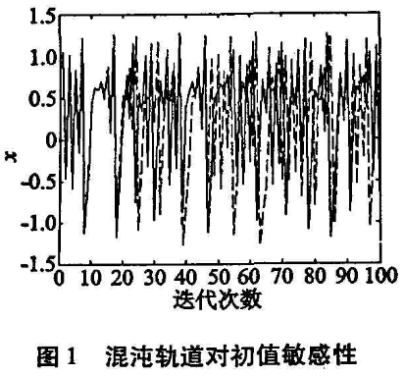
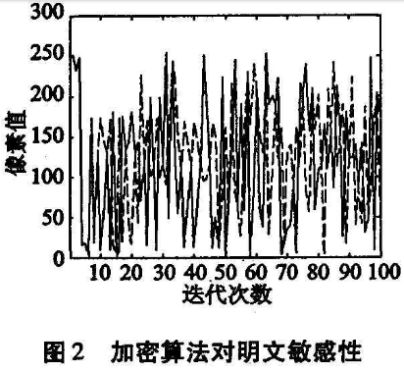
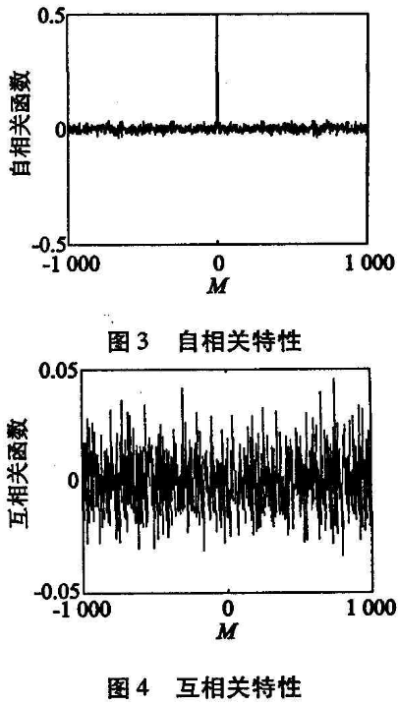
2)Henon映射具有优良的伪随机性,其轨道的演化是非周期、不收敛的,具有很好的随机性及不可预测性.取初值戈=0. 20,y=0.10(作为密钥后的一部分),对映射进行迭代。取序列长度N=5 000,相关间隔M=1000,对其混沌实值序列按公式(3)计算相关函数Rx(m):
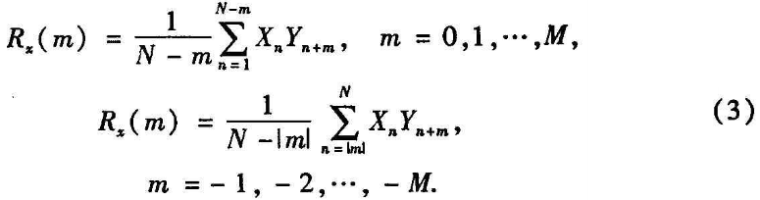
当取Y=X时,其非周期自相关如图3,改变初值为xo =0. 200 1,y=0. 1001时2个混沌序列的互相关特性如图4。可见其具有很好的密码学所需要的相关特性。
三、基于Henon映射的Feistel结构设计
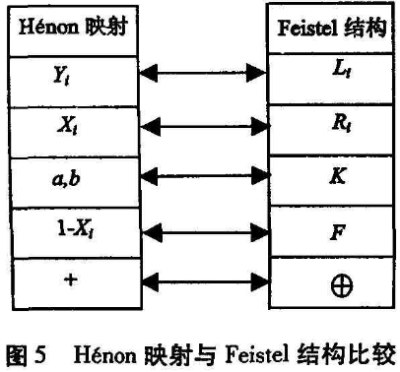
在Henon映射中,隐含了密码学中应用非常广泛的Feistel结构。通过比较式(1)和式(2),发现离散形式的Henon映射具有与Feistel结构非常相似的结构(见图5)。
为便于Feistel结构的设计及软件实现,将Henon映射写为:
![]()
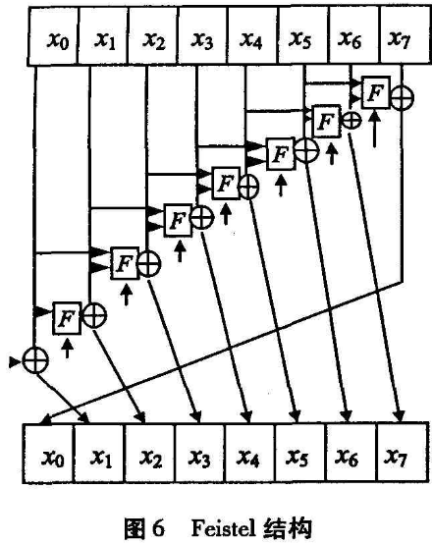
由此,笔者设计加密变换的Feistel结构如图6。
四、加密算法设计
加密算法中采取如下的分组密码模式:设B0为长为64位的分组,xi,o,xi,1,…,xi,7为一个分组Bi的8个字节,即Bi=xi,o,xi,1,…,xi,7。加密变换过程为对明文分组Bo进行r轮的相同变换,即:
![]()
其中,i=1,2,…,rk=1,2,…,8,f0=zi,o,X8=XO,第i轮的子密钥zi=zi,o,zi,1,…,zi,7控制第f轮的加密变换fo,fi,…Z是加密的轮函数,其形式为:
![]()
其中fo =zi,f1=f(xo,x1,z1),j=2,3,…,7,f:M→M,M={0,1,...,255}是从混沌映射导出的一个一对一映射函数,此算法中的混沌系统采用Henon映射。每轮的输出分组Bi=xi,o,x1,1,…,xi,7为下一轮的输入(最后一轮除外),因此,第r轮的输出Br=xr,o,xr,1,…,xr,7即为明文Bo的64位密文分组。
解密过程将加密变换逆运算,从密文Br,计算出明文Bo,注意在运用密钥时要与加密变换所使用的次序相反,解密变换为:
![]()
其中,i=1,2,…,r,k=1,2,...,8,f0=zi,o,X8=XO,f0,f1…f7是加密的轮函数。
五、加密算法安全分析
密码系统的核心是安全问题,怎样才能说一个加密算法是安全的呢?这个问题可以从理论和实践两个方面回答。
从理论上讲,一个安全的算法肯定具有“随机性增加”和“计算上不可预测”两个特性有关对“随机性增加”和“计算上不可预测”的严格定义超出了笔者所讨论的范围,且基于混沌的密码算法的安全性指标目前还没有建立,有待进一步研究。对所设计的算法而言,通过分析S-盒的非线性性和差分均匀性来证明。
从实践上讲,只有能够抵抗目前所有的密码分析攻击的算法才能说是安全的。但是,密码分析的方法浩如烟海,不可能一一穷举,只能证明其对最有效的密码分析的抵抗能力,从目前来看,差分密码分析和线性密码分析是最基本和最有效的两种攻击方式,估计一个分组密码抵抗差分密码分析和线性密码分析的能力也就成为评估这个密码算法安全强度的重要指标。
1、S-盒的差分均匀性
差分分析的过程就是寻找、暴露非线性变换中轮函数的差分不一致性,因此,差分密码分析最困难的步骤就是搜索r-1轮中具有最大或接近最大概率的差分。这样,就可以通过计算一个密码算法的差分逼近概率来评估其轮函数的差分一致性,定义差分逼近概率DPf为:
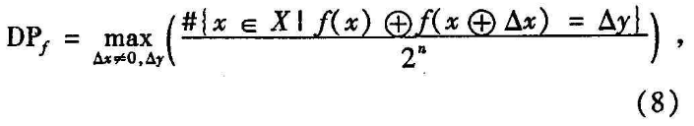
其中,X为满足要求的所有输入值的集合,2n为输入集合的元素个数事实上,DPf就是当输入差分为Ax,输出差分为Ay时的最大概率,减少Dpf的值就增加了差分密码分析的难度。根据计算,笔者所提算法的Dpf14/256 -2-4.4。
2、抗差分和线性攻击的评估
对分组密码抵抗差分密码分析和线性密码分析的能力评估,现有的做法主要有下面3种:
1)给出加密算法的最大差分概率平均值和线性概率平均值的一个上界;
2)给出密码算法的最大差分特征和线性逼近概率;
3)给出加密算法的最大差分特征和线性逼近概率的一个上界。
证明中采取在计算轮函数的差分逼近概率和线性逼近概率的基础上,通过估计差分活动轮函数的最小个数,给出算法的差分特征和线性逼近概率的一个上界,即通过估计算法式(5)的差分活动轮函数的最小个数,给出8轮差分密码分析的最大差分特征概率的上界。
小知识之Feistel
在密码学研究中,Feistel 密码结构是用于分组密码中的一种对称结构。以它的发明者 Horst Feistel 为名,而Horst Feistel 本人是一位物理学家兼密码学家,在他为 IBM 工作的时候,为Feistel 密码结构的研究奠定了基础。很多密码标准都采用了Feistel 结构,其中包括DES。Feistel 的优点在于:由于它是对称的密码结构,所以对信息的加密和解密的过程就极为相似,甚至完全一样。这就使得在实施的过程中,对编码量和线路传输的要求就减少了几乎一半。











