图像加密技术之小波变换域
如何确保基于网络的图像/视频信息的安全,是当前信息处理技术领域的亟待解决的难点和研究热点之一。为此我们利用混沌映射的随机性以及不可预测性,产生混沌序列矩阵对变换矩阵系数进行调整,再对系数进行置乱处理,然后利用信息隐藏技术对密钥进行隐藏,实现图像文件的高强度加密。
一、文件加密/解密系统
1、文件加密过程(如图1所示)

输入:原图像、载体图像1、参数1、参数2、参数3、…
输出:加密图像、载体图像2(其中包含密钥)
步骤1:首先对于大小为M×N的任意图像,其大小可能不是8×8整数倍,这时要对原图像进行边界扩充(添0),使得其大小为8×8的整数倍,其方法是在图像的边界填充0(黑色):再按照图2所示过程对图像进行连续三级小波分解。
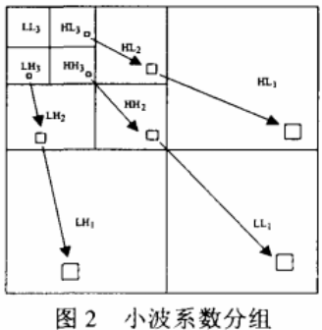
步骤2:将小波系数按照图2的顺序分为四组,即低频部分LL3、水平区域组(HL3,HLa,HLi)、垂直区域组(LH3,LH2,LHi)和对角线组(HH3,HH2,HHi),分别编号为组1、组2、组3和组4。当然还可以有其他分组方式。分组完成后,按照小波零树扫描方式(见图3)将每组数据变为一维数组。
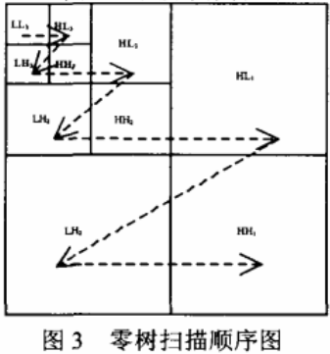
步骤3:生成混沌密钥模板矩阵。首先根据输入参数,选择混沌系统,并给定初始值,生成密钥模板,利用该密钥模板,分别对每组小波系数进行相应的调整。
步骤4:根据输入参数选择置乱方法,本文选择Amold变换与FASS曲线相结合,然后分别对小波系数进行分块和全局范围内的置乱处理,FASS方块大小及Arnold变换的次数,在参数中给出。然后将处理完的小波系数按照图2和图3的逆过程,将一维系数返回二维空间。
步骤5:根据用户需要(输入参数中给出),可以再进行步骤2-4的过程对小波系数进行再次加密处理。否则,将数据输入图像量化编码系统,进行图像数据的量化编码,或通过小波逆变换输出加密图像,同时输出解密密钥和伪装密钥,形成密钥包文件,它包含了所有的加密信息。
步骤6:将输出的密钥包隐藏在载体图像中,提供给终端用户,便于解密时提取密钥数据。
解密过程:
输入:加密图像文件、载体图像
输出:解密图像文件
首先,对输入的载体图像进行分类处理,识别出加密图像文件、载体图像和一般普通图像,然后通过运行特定的去隐藏程序,从载体图像中提取密钥包数据,同时进行用户端的解密认证程序,确认密钥包的有效性。密钥包有效后,提取解密密钥。将该密钥输入混沌解密系统,系统自动分析密钥,提取解密特征信息,得到加密参数,进行加密过程的逆过程,就可以实现图像文件解密,输出原图像。具体过程如图4所示。

二、仿真结果与分析
本文采用Lena512作为原始图像,选用Daubench-9小波进行三级小波变换;然后采用Hilbert非线性变换与Amold变换相结合进行小波系数的置乱处理,Hilbert变换划分子块大小为4×4、16×16、64×64三种,依次进行置乱处理:最后选择Logistic混沌系统,生成密钥模板。它的描述如下:
![]()
式(1)中,a称为分枝参数。当a∈(1.401115…,2)时,Logistic映射工作于混沌状态。具体参数为:a=1.6,x(1)=0.4,生成离散序列X(n),然后按照关系式(2)产生加密模板EK(n)和按照关系式(3)生成解密模板DK(n)模板。最后依据步骤4、5、6完成图像加密工作,得到图5(a)和(b)所示的小波系数密图和经过离散小波逆变换(lnversc Discrcte Wavclct Transform,IDWT)得到的Lena密图。
加密:

解密:

式(2)和(3)中,n=1,2,3,…,从序列中n=no(其起始位置no也作为密钥的一部分,此处no=310)处开始截取密钥模板Ek(n),长度与需要加密的小波系数个数相同。将密钥模板Ek(n)与小波系数进行点乘,完成对小波系数的加密。图5(b)为采用Daubechies-9直接对该加密系数进行IDWT变换的结果,得到一副非常混乱的Lena512密图,
原图像信息得到有效的加密处理。

1、破解实验
任何一种加密方法都要经过破解实验的检验才能证明是有效的。先取a=1.6,x(1)=0.4,no=310,按照式(3)生成解密模板Dk(n),将解密模板Dk(n)与加密小波系数进行点乘得到解密的小波系数,将其进行Daubechies-9的LDWT变换,得到图5(c)所示的一幅非常清晰、与原图一致的解密图。说明Lena图像能被有效地按照图1、图4的过程进行方便快速地加密和解密。再分别取a=1.600001,x(1)=0.4,no=310:a=1.6,x(1)=0.400001,no=310,得到的模板Dk(n)进行同样的IDWT变换,分别得到两幅仍然十分混乱的图像,见图5(d)和(e)。图5(f)是采用与图5(c)相同的解密模板,进行IDWT时采用Symlets9,同样得到一幅依然十分混乱的图像。在解密过程中无论是混沌密钥,还是小波变换参数出现问题,均无法达到正确解密的目的。
2、抗干扰实验
先对图5(b)所示的Lena密图加入随机噪声,然后再对其进行解码.解密实验,结果如图6。图6(a)是对密图5(b)加入随机脉冲噪声(椒盐噪声salt&pepper,强度参数0.01),图6(b)是在此基础上引入加性噪声(gaussian.强度参数0.01),图6(c)和(d)是对图6(a)和(b)的解密结果,可见图像上仍然存在非常严重的噪声痕迹,虽然图像的质
量下降了,但图像所要表述的内容已基本清楚了,通过进一步降噪和直方图均衡处理,图像表达的信息能够得到加强,见图6(e)。通过该方法加密的图像数据能够经受传输和存贮过程中的随机噪声的干扰和影响。

3、压缩实验
本文对加密后的DWT频率域数据进行零树小波量化处理,由于加密过程是在DWT低频系数中进行,在进行图像压缩编码时,根据当前的阀值TO,首先丢掉绝对值比TO小的系数,而DWT的低频系数的绝对值往往较火,在解码时采用与该系数最接近的TO整数倍的数值来代替。说明高压缩比处理过程只会造成解密图像质量的下降,不会对图像要表达的内容构成实质性损害。图6(f)是采用该量化方案,T0=16时,去掉所有小于16的系数,得到的解密图像,此时的压缩比(Compress Ratio,CR)~20,峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)=76.43.虽然图像中存在一定毛刺,但并不影响图像的视觉效果。因此,压缩对加密效果的影响不大,该加密方法可与JPEG-2000兼容,得到一种高效的基于高压缩比的图像加密方法。
4、密钥的隐藏
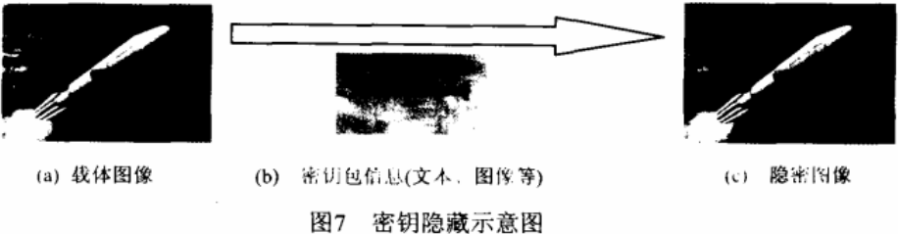
图7是密钥隐藏过程的简单说明,它将前面图像加密算法生成的密钥数据包(解密密钥与伪装密钥),通过特定的加密程序隐藏在一幅普通图像(载体图像)中,普通图像与包含有密钥信息的加密图像没有明显的差异。如图7(a)加入另外一幅图像(图7(b),称为秘密信息)后生成图7(c)的隐密图像,图7(a)与图7(c)的差别是人的肉眼
感觉不到的,只有通过计算机运行特定的解密算法才能检测秘密信息的存在。图7(b)的秘密图像大小为64.7k,载体图像大小为1.36M.效果非常好。如果待加秘的信息为文本文件或数字序列,信息量会更小,信息的隐藏效果会更好。
5、破解分析
经过前面的分析表明,Lena图像文件能被有效地加密和解密。要成功破译本文的Lena密图5(b),其关键是要获取密钥包数据文件和对密钥的成功解码,取得所有加密参数。由于本文采用加密图像信息与密钥信息分开保存,并实现密钥信息的伪装和隐藏,增加密钥的破解难度。下面假设一位密码攻击者想要破解密钥。他首先要从图
像序列中寻找哪张图像包含有密钥信息,由于包含有密钥信息的图像与不包含密钥信息的图像在统计直方图、色彩和纹理等方面没有有明显差别,通过肉眼无法判定该图像是否包含有密钥信息。只有通过计算机运行特定的程序才能将包含有密钥包信息的图片从图像序列中分离出来。没有特定程序或不知道算法,破解的难度可想而知,基本上不能进行下一步工作。再假设该位密码攻击者知道图像隐藏技术或通过某种方法从图像中分离出密钥包数据,但他得到仍然是一堆密码文件,其中虽然包含了密钥,仍然需要运行特定的解密程序才能得到密钥。此处的密钥也通过混沌加密处理,具有很强的随机特性,且采用的混沌系统的初始值和参数的取值范围为整个实数域,如果采用穷举法,成功破解密钥的机会为零。
如果攻击者不去破解密钥,而直接对图像数据流进行解密,且又不知道采用了变换域加密技术的情况下,解密过程根本无从谈起:如果他知道采用了变换域且知道采用了何种小波变换,此时的关键技术就集中在置乱变换的解密和对混沌序列的破解上面。在对置乱变换解密的过程中,只是将F(x,y)的位置打乱,未对相应的图像信息进行处理,此时可以采用穷举法,需要运算的次数为:对于16×16的图像,运算的次数为256r≈8.6×10506;对予256X256的图像,运算的次数为65536!≈5.2×10287193,这已经是一个非常大的数据了,以目前的万亿次计算机的处理能力。5.2×10287193/1015≈5.2×10287178(S),此时已经无法满足解密要求。本文还采用了混沌序列对特定位置的值进行了特殊处理,由于混沌系统的初始值和参数值的取值范围为整个实数域,如果采用穷举法,目前还没有计算机能够完成这两个任务,因此成功破解密钥的机会仍然为零。
在另一个方面,由于算法的密钥为K= (aio,xio,a20,x20, a30,x30,n1,n2,n3,n4),其中a和x为混沌系统的参数和初始值,n1为混沌序列的起始位置,n2为采用的变换域方法,n3为采用的置乱处理方法,n4为采用的置乱处理变换的次数和顺序,这些参量都可以任意选择,因此算法密钥的改变十分方便。因此,该加密算法不仅对唯密文攻击免疫,而且选择明文攻击,也不能对该算法的安全性构成威胁。
小知识之椒盐噪声
椒盐噪声是由图像传感器,传输信道,解码处理等产生的黑白相间的亮暗点噪声。椒盐噪声往往由图像切割引起。











