针对单一混沌映射有可能退化为周期问题以及图像置乱加密计算量大的缺点,提出了一种基于复合Logistic和Chebychev映射与小波变换的图像加密算法。该加密算法根据密钥控制复合混沌序列的初始参数,生成混沌序列,进而对图像文件进行置换加密,然后对加密后的图像文件进行小波分解,再对小波近似系数进行置乱加密。
一、加密算法描述
1、混沌置换加密过程
混沌应用于数字图像文件加密的关键是混沌序列的随机性,针对低维混沌序列的短周期问题,笔者采用由Logistic混沌映射和Chebychev混沌映射复合生成混沌序列,对混沌序列的初始参数则通过m序列来进行控制,加密过程如下。
(1)采用Logistic混沌子序列为初始混沌序列,其模型为:
![]()
其中,μ为分岔参数;xn为初始参数。当3.569 945 6<μ≤4时,不同的初始状态xo生成的序列是非周期、不收敛、不相关的,并对初值非常敏感。Logistic序列工作于混沌状态。
(2)采用Chebychev混沌序列对Logistic序列进行改进,构成复合混沌序列。Chebychev混沌序列的方程为:
![]()
当参数k=5时,Chebychev映射工作于混沌状态。用此混沌方程的迭代输出作为Logistic映射的控制参数,增加μ的变化量,从而增加Logistic序列的周期。Chebychev映射的迭代值域为[-1,1],应通过线性映射变换到Logistic映射参数μ的变化区间。
(3)采用m序列生成随机数,控制两混沌序列的初始参数,将生成m序列的初始值作为密钥。m序列是由线性反馈移位寄存器产生的周期最长的二进制数字序列,也称为最大长度线性反馈移位寄存器序列,是一种实现方便的伪随机数生成方法。由于根据密钥生成伪随机数一般不在Logistic和Chebychev映射的参数范围内,因此需要将生成的随机数分别向Logistic的参数范围(0,1)和Chebychev的参数范围[-1,1]分别作线性映射,其输出作为Logistic序列和Chebychev序列的初始参数。
(4)将Chebychev序列的输出作为Logistic映射的控制参数,m序列生成的随机数向Logistic序列作线性映射的输出作为Logistic的初始参数,生成复合混沌序列。
(5)将生成的混沌序列与原始水印图像进行按位异或,生成置换加密后的图像。
2、基于小波的置乱加密过程
图像置乱是利用某种算法将一幅图像各像素的次序打乱,但像素的总个数不变,直方图不变。已提出的图像置乱方法有:Fassy曲线,Hilbert曲线,Gray码,Conway游戏,Tangram算法,IFS模型,Arnold变换和幻方变换等。本文选择Arnold变换作为图像置乱方法,考虑到对图像置乱计算量较大,首先对经混沌置换后的图像进行小波变换,然后再对小波变换的近似系数进行置乱。具体过程如下:
(1)选择db3小波对图像进行三级小波分解,可得10个分解系数矩阵,设原始图像为NxN大小,则分解后近似系数矩阵大小为N/8×N/8,因此对分解后的近似系数矩阵进行置乱可大大减小计算量,又由于近似系数对图像视觉的影响起主要作用,因此选择对近似系数进行加密也是合理的。
(2)对近似系数矩阵进行Arnold变换。Arnold变换是一种自同构变换,又称猫脸变换(Arnold's cat map),构造如下置换方程:
![]()
式中,xi,yi表示空间坐标,对地图像,xi,yi表示图像像素的位置坐标,k为随机数,由密钥通过m序列生成,当k大于N时对矩阵进行取模运算,mod表示取模运算。
将经Arnold变换后的近似系数矩阵与(1)中小波分解后的另9个细节系数矩阵进行小波重构,得到最终的加密图像。
二、实验结果与分析
我们在Visual C++6.0下实现了上述算法,选择Lena图像(256×256,256灰度级)作为仿真对象,仿真结果如图1所示。其中图1(a)为原始图像,图1(b)为加密后的图像,图1(c)为密钥正确解密后的图像(密钥为123456),图1(d)为密钥错误时的解密图像(密钥为123457)。从仿真结果看出,本加密算法能有效地加密/解密图像文件,即使密钥稍有不同,也不能解密出图像且看不到原图像的任何信息。

图2(a)为原始图像的直方图,图2(b)则为加密后的图像直方图,可以看到原始图像被加密后直方图被均匀化了,这表明加密算法具有不错的密码学特性。
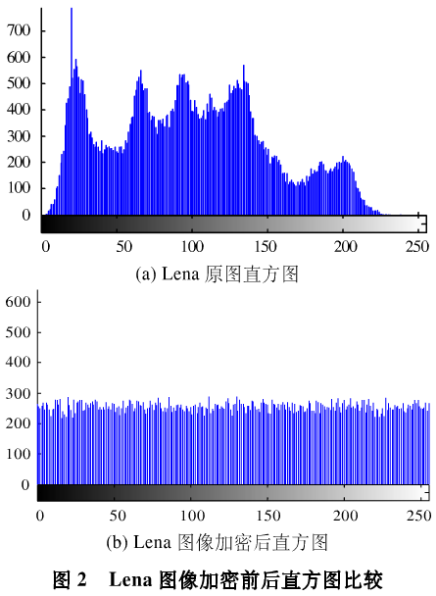
与普通的基于混沌加密算法相比,本图像加密算法具有以下优点:
(1)图像加密算法采用复合混沌序列,其保密性要优于普通的低维混沌序列,而计算量则小于高维混沌序列。这是由于低维混沌序列很容易受到混沌模型重构方法的攻击,而复合运算掩盖了混沌子序列的分布特性,改变了原混沌系统的动力学行为,有效地抵制了模型重构攻击,从而使其保密性得到提高。
相对于高维混沌序列,复合序列的计算量较小,因为通常的低维混沌系统模型都是用代数方程描述的,求解速度很快;而高维混沌一般为复杂的微分或差分方程,求解的复杂度和计算量都比较大。
(2)图像加密算法把置换加密放在置乱加密之前可以增强置乱加密的抗攻击能力,原因是置换加密的结果隐蔽了置乱加密,所以靠收集图像特征的置乱加密破解方法是不可行的,而相反序列则会增强置换加密。
(3)图像经典的加密方法通常只在空域或频域加密,本文采用的算法在空域和小波变换域双重加密,改善了加密效果,增大了加密强度,单纯在空域或频域的种种破解尝试都将是困难的。置换加密使用了性能更好的复合序列,弥补了置乱加密抗攻击能力较弱的缺点,为兼顾加密强度和减少计算量,用户可根据需要选择置换加密和小波分解层数,这些特点使得该算法具有良好的适用性。
图像加密算法的不足是,要经过两次混沌映射计算以及生成m序列,与一般单映射混沌加密系统相比,其计算量显得较大。
小知识之小波变换
小波变换是近年来在图象处理中受到十分重视的新技术,面向图象压缩、特征检测以及纹理分析的许多新方法,如多分辨率分析、时频域分析、金字塔算法等,都最终归于小波变换(wavelet transforms)的范畴中。











