基于Hilbert曲线与Gray码,我们提出两种针对任意矩形彩色图像的加密算法,其一是对图像像素点的空域置乱,其二是对像素点的24位R、G、B分量的空域置乱,解密过程即加密过程的逆。
一、Hilbert曲线
1、二维Hilbert曲线
经典的二维Hilbert曲线的描述如下:首先将正方形四等分,求出各个小正方形的中心,并将它们连接,其次,将各个小正方形再细分为4个相同的小正方形;并连接各个小正方形的中心;……;按照这种分法不断细分下去,并按一定规则一一连接,就可以得到如图1的Hilbert曲线。
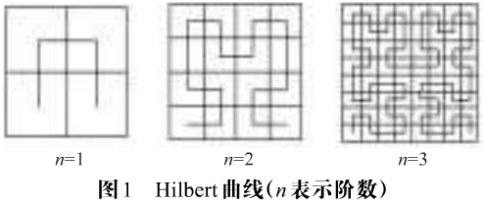
2、 三维Hilbert曲线
一阶三维Hilbert曲线构造方法:将一立方体等分成8个小立方体,把8个小立方体的中心按一定的次序连接成一条曲线,即连成图2的三维单元。以三维单元为基础来构造高阶三维Hilbert曲线,因为它是整个曲线形状的基础,所以又称它为基元。
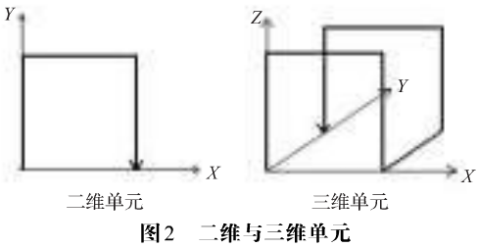
n阶三维Hilbert曲线构造方法:将一立方体等分成8个小立方体,每个小立方体用n-1阶三维Hilbert曲线代替,然后按基元一样的次序连接这8条n-1阶三维Hilbert曲线。为使曲线更精美,对8条n-1阶三维Hilbert曲线作适当的旋转使连接的首尾平行于一轴线,如图3。
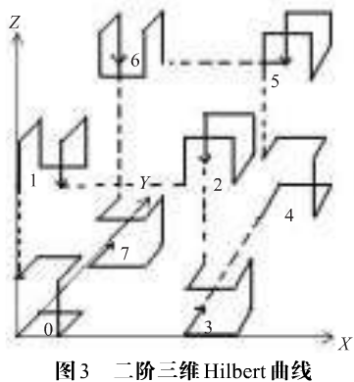
3、Hilbert曲线图像置乱
传统意义上利用Hilbert曲线实现图像置乱的思想:对图像像素点按Hilbert曲线的规则遍历,将其存入一维序列中,再重新排列生成置乱图像。实践证明,这种置乱算法应用性不强,如10×10大小的图像则不能按此规则置乱。
两种比较典型的算法,一种(算法1)是对非正方形图像分成四块满足Hilbert遍历规则的正方形块,分别是左上角,左下角,右上角,右下角,使得图像的每一部分至少
被置乱一次n1,这种算法比较繁琐,增加了算法的时间复杂度。另一种(算法2)是对前者的改进,将像素点的R、G、B三色分量排列成一维序列,对于M×N的数字图像,直接把3×M×N个图像数据排列到一维数组pl[]中,假如2n-1<3×M×N<2n,则可对pl[]补上(2n-3×MxN)个值为-1的数据,选择一条n阶Hilbert曲线进行置乱处理,再把值为-1的数据去掉,余下的就是置乱后的图像数据。该加密算法类似于对图像像素进行填充,增加了原图变换的工作量,如图4。
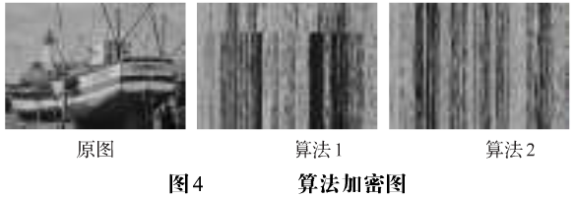
二、Gray变换
1、Gray码
定义1对于任意一个非负整数u,其二进制码记为纠=(uup-1up-217...u0u1)2,令:
![]()
i=1,2,…,p-1,则得到一个二进制表示的整数gu=(gpgp-1--g1go)2,变换式(l)称为Gray变换,gu称为的u的Gray码,其中运算“0”为模2加法。
2、Gray码图像置乱
(1)基于位置:对于MxN阶数字图像,按一定顺序对像素点进行编号,利用(N进制)Gray码变换置乱图像。
(2)基于色彩:保持像素点的位置不动,改变像素点的灰度(RGB)值。此时应先把像素点的R、G、B分量值用8位二进制码表示,再利用二进制Gray码变换。
如图5,置乱图1(64x64)是基于位置的变换,置乱图2是基于色彩的变换。

值得注意的是:对于基于位置的Gray变换,选取N进制和N进制的位数比较重要,如图像大小为3 x4-12,则像素点不能实现位置置乱的一一映射。而基于色彩的Gray变换,加密效果十分差,且周期很短,在实际中不具有应用性。
三、矩形分割算法
将任意一个矩形图像的长、宽(如果是长方体则是长、宽、高)通过矩形分割算法,对这两(三)个数分裂相同的次数,使长、宽(长、宽、高)分别分成2n(n=1,2…)段,即可将一个矩形(或者长方体)分成2nx2n(或者2nx2nx2n)块,将这些分裂出来的矩形块(或长方体块)作为一个单元,这些单元满足n阶二维(或三)Hilbert曲线遍历规则。
分割算法的详细步骤如下:
对任意整数m1,m2,做式(2)运算:
![]()
假定被分裂的数为l,通过一次分裂出来的两个数为l(0)l(1),则分裂规则为:
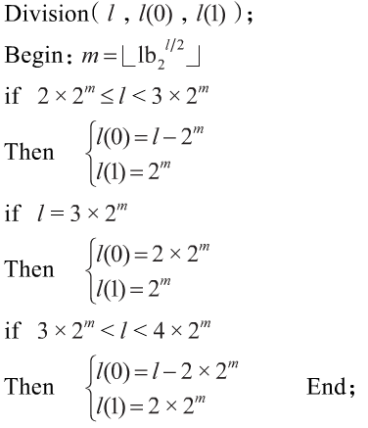
对m1,m2同时分裂M= Min(Mm1,Mm2)次,即可将两个数分别分裂成2M等分。如图6通过两次分裂分成4x4=16小块。

四、图像加密新算法
1、二维Hilbert曲线混合Gray码空域重组矩形图像像素点
(1)图像分块
将图像的宽、高按矩形分割算法将图像分成2nx2n小块,将小块利用n阶Hilbert曲线遍历,达到对小块的置乱。由于矩形分割算法的特点,任意矩形图像分出来的块,最多只有一行块和一列块(或者只有一行块,或者只有一列块,或者没有)内的像素点的个数不是2n(n∈N),如图6为第一列块和第三行块内的像素点的个数不为2n(n∈N)。
(2)对小块内像素点的处理
①若小块内的像素点的个数为2n(n∈N),则可以选择n位二进制位对小块的像素点进行Gray码位置置乱,假定图像块大小为2x4,对小块内像素点进行编号(0,1,…,7),从而用3位二进制Gray码变换重新排序像素点。
②若小块内的像素点的个数不是2n(n∈N),比如3x3,则利用Gray色彩置乱顺序遍历小块内的像素点。
实验证明,小块内像素点的Gray码变换主要是降低像素点之间的相关性,单从视觉上来说,即使不对小块Gray变换,图像的置乱效果也是很不错的,如图7。

2、三维Hilbert曲线混合Gray码空域重组矩肜图像24位
(1)将像素点对应的R、G、B分量值转换为8位二进制数,把图像分成24个位平面,将像素点的24个位存入三维序列P3[k,i,j]中,其中i,j对应像素点的坐标,0≤k<24,如图8。
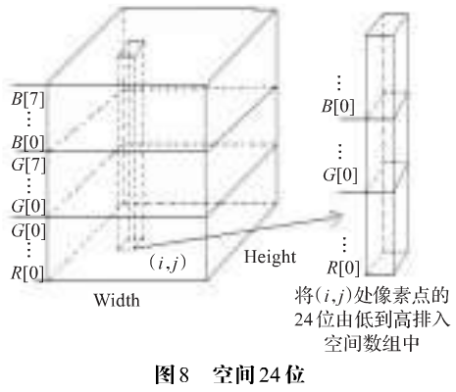
(2)将width,height,24这三个数按分割算法进行分裂,将长方体划分为2nx2nx2n个小长方体块,对应胛阶三维Hilbert曲线遍历规则。
(3)对小长方体块内二进制位数据的处理,与上节中的对小块处理类似,只不过从平面延伸到了空间,规则为:
①若小长方体块内的元素个数为2n(n∈N),则选择Gray码位置置乱。
②若长方体块内的元素个数不是2n(n∈N),则不做变换,因为小块内存储的元素是二进制位,如图9。

五、加密算法分析
(1)创新性
利用三维Hilbert曲线对彩色图像的24位空域置乱,通过图9可以发现,对彩色图像24位的空域置乱可以达到非常好的置乱效果,大大降低了像素之间的相关性。
(2)加密算法执行效率
算法在.net 2005环境下编译运行,机器配置为AMD 64Processor 2800+,内存1GB。对238×170图像(图4的原图)分别用4种算法变换一次所需要的时间如表1。
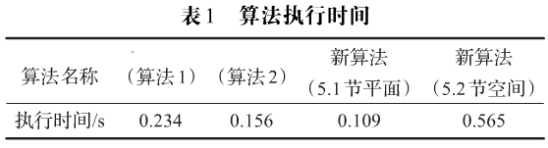
通过表1发现,基于二维Hilbert变换的新算法较这2种算法执行效率都要高,而基于三维的Hilbert变换则要慢很多,这与三维空间中的数据量有关,但是其置乱效果是非常好的。
(3)安全性
由图4、图5、图7、图9可以看出,基于像素点的空间位置置乱可能会给解密者留有一个信息:如果原图像是灰度图,则加密后的图像一定是灰度图。然而基于24位的空域置乱加密后则不再是灰度图,置乱图接近混沌状态,大大提高了加密的可靠性。
小知识之遍历
所谓遍历(Traversal),是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,是二叉树上进行其它运算之基础。当然遍历的概念也适合于多元素集合的情况,如数组。











