近年来,光学加密技术不仅针对单幅图像文件加密,多图像文件加密也成为研究热点。为此,本文提出一种基于横向叠加多图像加密算法,并结合改进后的多维数据文件加密系统(VOI)光学加密系统完成多幅图像文件加密。由于多幅图像为横向叠加,避免了纵向叠加所产生的加性串扰,提高了解密图像的像质。
一、加密算法描述
1、加密算法
本文提出的多图像加密由两部分组成,加密图像采用目前市场上普遍使用的标准二维码图像,读取传输均可通过手机,使用方便,具有实用价值。第一部分通过计算机完成四幅二维码图像的横向叠加,该部分的物理模型如图1所示。
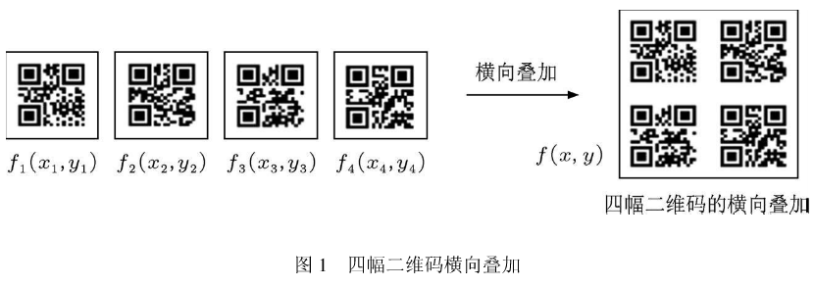
f1(x1,y1);f3(x2,y2);f3(x3,y3); f4(x4,y4)分别表示待加密的四幅二维码图像,经编码横向叠加的二维码图像由,f(x,y)表示从图1中可以看出,f包含了f1,f2,f3,f4的所有信息,其过程如(1)式:
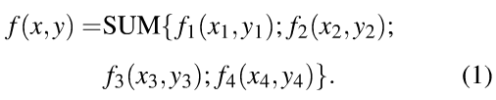
第二部分为改进后的VOI系统。加密系统如图2所示。
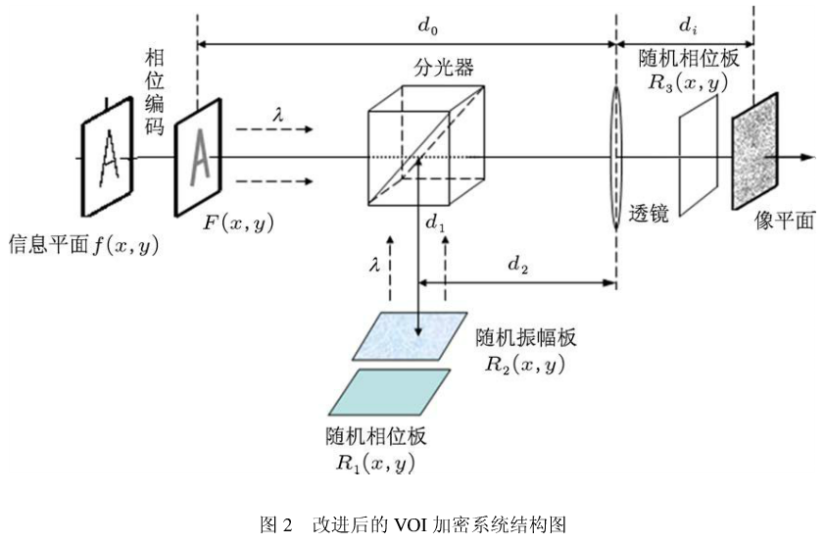
信息平面处放置横向叠加图像f(x,y),将其相位编码后得到图像用F(x,y)表示,随机生成相位模板为R1(x,y),随机振幅模板R2(x,y),对R1(x,y)进行振幅调制,生成随机模板信息R(x,y)。算法表示如下:
![]()
根据傅里叶光学,波长为λ的虚拟光波从物平面到透镜前表面和虚拟光波从透镜后表面到像平面的传播过程可用菲涅尔衍射变换描述。因此,从图2可以看出,F(x,y)经过衍射距离为do的菲涅尔衍射变换后,在透镜前表面生成N1(x,y);R(x,y)经过衍射距离为(d1 +d2)的菲涅尔变换后,在透镜前表面生成N2(x,y);通过N1(x,y)和N2(x,y)在透镜处的非相干叠加,得到N(x,y),N(x,y)通过透射率为t(x,y;f)的透镜,经距离为di的衍射,再由随机相位板R3(x,y)的相位调制,在像平面处得到密文
U(x,y)。若FrTλ,do{}表示波长为λ,衍射距离为d的菲涅尔衍射变换,则上述算法可表示为:
![]()
![]()
2、解密算法
解密算法是上述两部分算法的逆过程,用IFrTλd{}表示菲涅尔逆变换,首先对随机相位板R3(x,y)和透镜做逆变换,得到透镜前表面的叠加信息DeN(x,y)过程如下:
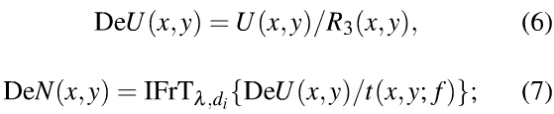
再减去R(x,y)在透镜前表面形成的菲涅尔衍射影响,得到信息平面F(x,y)在透镜前表面形成的菲涅尔衍射DeN1(x,y):
![]()
再经过菲涅尔逆变换和相位编码的逆变换,得到信息平面f(x,y)的解密结果:
![]()
最终将得到信息分割成原来的四幅二维码,表示如下:

3、基于峰值信噪比的评价方法
本文采用峰值信噪比(PSNR)进行解密图像的质量评价,以判定系统的加密解密效果,计算方法为:
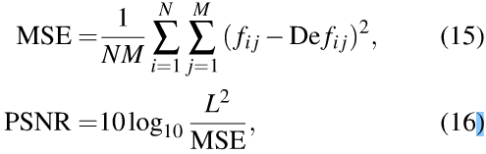
其中MSE为均方误差,是加密与解密图像之间总的灰度差,可以理解为噪声信号;PSNR是峰值信号与噪声的比值,比值越大,两幅图像相似度越高,当高于35-40时,肉眼分辨不出差异;N和M是图像矩阵维度数,L是图像最大灰度值。通常8 bit的图像L为255,若图像矩阵像素点的灰度值类型是1或0,则L为1。
改进后VOI系统除原系统的密钥(λ,do,d1,d2)外,增加了随机振幅板R2(x,y)和随机相位板R3(x,y),增大了系统的密钥空间的维数,增强了系统抵抗暴力攻击的能力,提高了系统的安全性。
三、计算模拟与分析
1、加密解密算法正确性分析
本文采用matlab仿真,加密对象如图1所示f(x,y),波长取值为632.8 nm,每幅图像有效采点数为116×116,衍射距离{d0,d1,d2}分别取为{10,20,10}mm。叠加图像相位编码F(x,y)如图3(a)所示,密文U(x,y)如图3(b)所示,相位编码解密DeF(x,y)如图3(c)所示,叠加图像解密Def(x,y)如图3(d)所U(x,y)如图3(b)所示,相位编码解密DeF(x,y)如图3(c)所示,叠加图像解密Def(x,y)如图3(d)所示,解密图像Def1 (x1,y1),Def2(X2,y2),Def3 (x3,y3),Def4 (x4,y4)分别如图4(e)一(h)所示,如图3所示,四幅解密图像的PSNR分别为156.0728,155.8671,156.0261和155.7347,因此,解密图像与原图基本一致,表明了本加密系统的有效性。

2、安全性分析
在改进方法一中,通过在随机相位板R1(x,y)中叠加随机振幅板R2(x,y),提高了系统的安全性。事实上,对原VOI系统,当攻击者已知密文U(x,y)和除了随机相位板R1(x,y)外所有密钥(λ,do,d1,d2)时,采用任意随机相位模板R1'(x,y)解密,解密结果如图4(a)所示,原图信息基本还原,且解密图像的PSNR值为14.04;但在改进后的VOI系统中仅添加了随机振幅板R2(x,y),针对上述情况,解密结果如图4(b),解密图像PSNR值为7.01。若攻击者已知随机振幅板和随机相位板的叠加方法,同时生成两个随机板R1’(x,y)和R2’(x,y)解密,其结果如图4(c),PSNR值为7.05.综上所述,攻击者已知密钥和密文,未知随机信息,原VOI系统的解密结果含有原图的大部分信息,改进后的VOI系统解密图像基本是噪声,比较前后两系统PSNR值,改进后的VOI系统安全性有所提高。

在改进方法二中,通过添加随机相位板R3(x,y),提高了系统的安全性。事实上,若攻击者已知原VOI系统的所有密钥(λ,do,d1,d2,R1(x,y))和密文U(x,y),未知随机相位板R3(x,y)直接进行解密,解密结果如图4(d)所示,PSNR值为2.08;若已知加入R3(x,y),产生任意随机相位板R3’(x,y)解密,结果如图4(e)所示,PSNR为负值。
上述分析讨论表明,原VOI系统对抗暴力攻击的能力弱,在随机相位板未知的情况下,攻击者可以还原被加密的原始图像信息,达到窃取图像信息的目的,破坏了信息的机密性,而改进后的VOI系统能够抵抗暴力攻击,提高了系统的安全性。
四、加密算法分析
作为面向数据加密应用的算法,其鲁棒性和安全性是算法的重要特征。本节分析改进后的VOI系统对抗各类噪声以及密钥失真时所表现的性质,首先分析算法对抗各类噪声的鲁棒性,本文模拟了高斯噪声、泊松噪声、椒盐噪声等对算法的影响。相比较三种噪声,因算法对高斯噪声效果相对较差,选择高斯噪声作为分析对象,均值和方差取值分别为0,0.01。图5为高斯噪声加到密文上时的解密结果,四个二维码解密结果的PSNR为64.2307,75.7968,60.5291,66.2979。可以看出,信息丢失少,解密效果好,因此本算法对抗各类噪声的能力强。

下面分析在密钥失真情况下系统的安全性,首先分析系统原有的四个密钥{do,d1,d2,λ)对安全性的影响,然后讨论增加的密钥对{R2(x,y),R3(x,y))对安全性的影响。图6(a),(b),(c)显示了将密钥中的衍射距离{do,di,如)改变0.3,0.4和0.5 mm时(假设其余密钥都正确),分别解密出的DeF(x,y);图4(d)则显示了密钥λ发生变化时,解密出的DeF(x,y)。当do改变0.3 mm时,图像解密的质量比较差,原图像的特征已经被丢失,解密图像的PSNR只有3.8517,这表明本文提出的加密算法和解密算法对密钥do是不敏感的,该密钥可以起到增强算法安全的作用;但是当d1改变0.4 mm时,解密出的结果能大致看出有四幅二维码,显示了原始图像的轮廊,泄露了少许信息,此时PSNR为7.0428;而当d2改变0.5 mm时,解密出的结果非常清晰,PSNR甚至达到49.6170,原图信息完全泄露,表明加密算法和解密算法对该密钥敏感,密钥的微小变化就可以得到原始图像的部分信息,破坏了算法的机密性.当解密密钥允取500×10-5 111时,解密结果同样也是很差的,PSNR只有6.7680。

从上述分析中可知,系统密钥(do,d1,d2,λ)中,加解密算法对d和λ不敏感,这两个密钥的微小变化解不出加密的图像信息。反之,密钥d对系统几乎没有什么保护性,攻击者在不需要知道它的情况下,可以解密出较清晰的原始图像。因此原VOI系统的密钥安全性不够强,而本文希望通过增加两个随机模板作为新密钥来增强系统的安全性,下面讨论其对加密算法安全性的影响。
当随机振幅板R2(X,y)失真时,解密结果如图7(a)所示,PSNR值只有5.9134;当随机相位板R3(x,y)失真时,解密结果如图7(b)所示,PSNR是负值。从解密图像可以看出,当附加密钥{R2(x,y),R3(x,y)}失真时,解密质量非常差,几乎看不出任何原图信息。

因此,可以看出,在系统的原有密钥(do,d1,d2,λ)中,如的保护性较差,无法保证算法的安全性,通过附加密钥对随机振幅板R2(x,y)和随机相位板R3(x,y)可以弥补该缺陷,提高了系统的安全性。
小知识之VOI
VOI(Vendor Owned Inventory,供应商拥有的库存),是企业实现供应零库存的一种常见模式。其基本实现形式为:供应商按照一定的计划组织备货,并把物料补充到企业可直接取用的仓库中。此时,对应物料的所有权仍然属于原供应商,还不算是企业的资产。但企业可根据自己的需求随时领用,并在领用出库时实现物权转移。最后,企业按约定的结算期限与供应商按实际领用量进行结算。








