随着图像技术的发展,图像的安全性问题越来越受到人们的关注。由于图像特有的属性,比如存储空间大、相邻像素之间具有很强的相关陛等,使得一些针对文本文件的加密方法如DES、IDEA、RSA等现代加密技术,不能完全满足图像文件加密的需要。其二维可逆映射的压缩过程分水平压缩和垂直压缩两种,折叠过程为对角线折叠。通过对图像的拉伸和折叠处理,实现图像文件的加密。
一、二维可逆映射原理和加密算法
图像置乱加密算法是通过二维可逆映射实现的。该映射利用了图像的一个重要性质:像素能通过插入到其他像素之间从而压缩为线。设图像大小为MN。通过映射首先将原图像拉仲为长MN的直线,然后再折叠成一个MN的图像。如图1所示,(a)为水平压缩映射,(b)为垂直压缩映射。
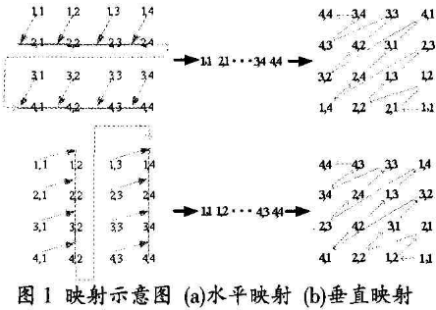
设图像大小为MxN,设A(i,j) j=0,1,2,…。N-1,i=0,1,2,…,M-I为图像中的任意一点,L(i),i=0,1,…,MN-1为将A(i'j)拉伸后的一维向量。
fix(X)是取最接近于X的整数。
1、缩算法
(1)水平压缩算法
如图1(a)所示,水平压缩映射算法如下:
首先定义函数:
![]()
则水平压缩算法为:
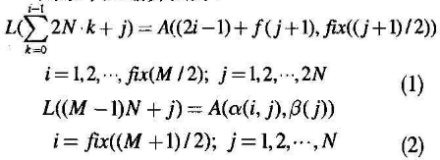
(2)垂直压缩算法
如图1(b)所示,垂直压缩映射算法同水平映射算法的公式形式上很相似,推导过程也类似。
2、折叠算法
如图1所示,对角线折叠算法如下:
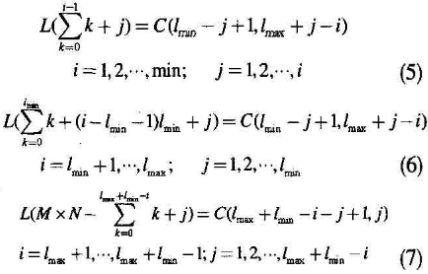
式中,lmin表示M和N中的较小值,lmax表示M和N中的较大值。
二、使用二维可逆映射实现图像文件的加密和解密
可将每个子映射的映射次数作为密钥Key。如Key=1234,表示图像依次水平映射1次,垂直映射2次,然后用水平映射3次,最后用垂直映射4次。为了保证加密效果,每一个部分密钥值都小于10。
图像加密算法所采用的扩散函数为:
![]()
式中,A(i,j)是指扩散前每一个像素的值。A(i,j)为扩散后的像素值,256灰度图L=256。
图像加密算法分为三步:
1、利用密钥及算法(1)~(4),将图像A(i,j)拉伸成一条直线1(i),i=0,1,…。MN-1。
2、利用算法(5)一(7),将直线折叠,得到置乱图像C(i,j)。
3、利用扩散函数,对置乱图像进行处理得到密图。
图像解密算法与加密算法相反,解密过程与加密过程对称,且解密密钥与加密密钥相同。
三、加密实例和安全性分析
如图2所示,对lena 256灰度图文件进行加密。为了研究二维可逆映射的加密效果,没有加入扩散函数。此时,加密系统仅仅置乱图像,没有改变图像的像素值(直方图不变)。
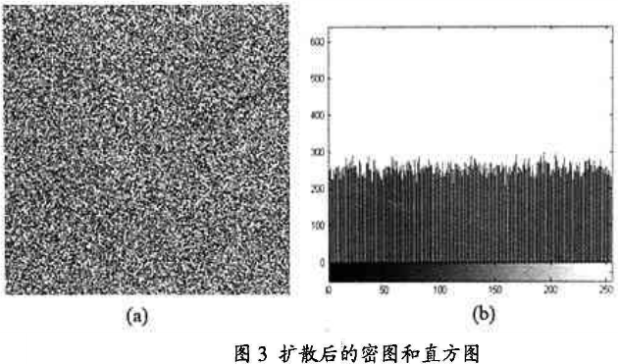
如图3所示当Key1=1时,图像已没有原图特征。当Keyr1234567890123456时,密图像素平均分布,加密效果良好。

1、安全性能分析
密钥空间分析。由于最基本、最流行的破解方法是对密钥进行穷尽搜索。密钥空间大是加密算法安全的前提。加密算法的密钥空间如表1所示。研究表明,密钥空间大小只和密钥长度有关,在理想情况下(计算速度允许)。可认为密钥能无限增加。

密钥敏感度
当加密密钥Key=1234567890123456加密时,用解密密钥Key1=1234567890 123455 和Key2 =12345678901 23457分别解密。即使加密密钥和解密密钥仅一位有最小的差异,也无法解密图像,证明对密钥差异非常敏感。
相关性统计分析
由于原始图像相邻像素之间具有很强的相关性。如果密图相邻像素之间相关陛变小,说明密图安全性变强。我们用下列两个公式计算他们的相关系数:
![]()
![]()
式中x、y为两个相邻点的灰度值。
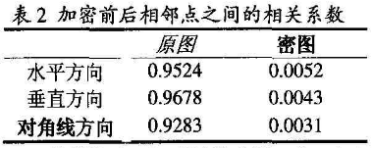
原图的相关系数为0.9524。加密之后的相关系数为0.0052,证明密图相邻像素之间相关度接近于零。其他相邻点的相关系数如表2所示,说明密图相邻像素之间相关性很小。
2、扩散算法
仅对图像进行置乱,而不改变像素值是不安全的,很难抵御明文攻击。因此为了增强加密算法的安全性,增加扩散函数。见公式(10)。加密后,密图和直方图分别如图4(a)、(b)所示。
四、与其他混沌加密技术的比较
和其他混沌映射比较。具有:
1、更大的密钥空间
如Baker map最大为2N-1(N为图像的宽),而该加密的密钥空间理论上只和密钥长度有关,只要计算速度允许,秘钥长度可随之增加。
2、对密钥变化更敏感
该加密算法将密钥设计为整个图像拉伸、折叠的数目,因此只要秘钥稍有变化,密图就会截然不同。但其他二维混沌映射基本都将图像分块的数目设计为密钥,拉伸、折叠操作都是对部分图像进行的。因此,用相似的密钥可以解密密图,降低了加密安全性。
3、加密算法更加简单、清晰,易于实现
如Baker map的一般形式下的加密算法具有非常复杂的形式。而该加密算法非常简单,易于实现。
4、加密速度快,能够实现实时加密
在一台Pentium M l.3CHz的笔记本电脑上仿真表明,未优化的二维可逆映射的VC程序,运行速度约为3Mbps。能满足实时加密需要。
使用该映射的优点为:该二维映射的加密算法非常简单,容易编程实现、二维映射可逆、基于二维可逆映射的加密,解密算法没有信息损失、加密的密钥理论上没有限制,在速度允许的前提下,可以为任意长度、密图和原图大小一致,没有大小差异、能满足实时需要,适合大尺寸图像加密、加密算法容易硬件实现等。
小知识之置乱
所谓“置乱”,就是将图像的信息次序打乱,将a像素移动到b像素的位置上,b像素移动到c像素的位置上……使其变换成杂乱无章难以辨认的图像。











