图像文件双重加密算法是一种基于傅立叶变换和Fibonacci变换的双重图像文件加密方法,相对于传统的傅立叶变换加密方法,双重加密方法的安全性更高,计算量更大。但由于Fibonacci变换是时域上的置乱,计算量比其他频域变换少,这种双重加密算法在安全性和计算量方面求得一个平衡。
一、傅立叶变换和Fibonacci变换
1、傅立叶变换
傅立叶变换是一种把信号从时域变换到频域的变换方法,对于二维的图像信号,傅立叶变换公式为:
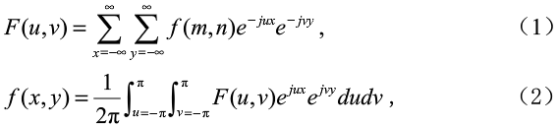
2、Fibonacci变换
(1)Fibonacci数列
如果定义F1_=1,F2 =1,E=Fn_i+Fn-2,n≥3,则数列{Fn}就是Fibonacci数列。
(2)Fibonacci变换
设Fn和Fn+1,是两个Fibonacci数列中相邻的数,则Fibonacci变换为:
![]()
其中k=0,1,2,…,Fn+1-1。
利用Fibonacci变换置乱一维信号后,可以使这个信号能量均匀分布在时域内,形成杂乱无章的信号,达到加密的目的。Fibonacci还具有周期性,即对一个信号做相同的
Fibonacci变换N次后可以精确的恢复出原信号。
二、图像文件的双重加密算法原理
1、图像文件加密方法
基于改进的傅立叶变换图像文件加密方法和Fibonacci变换的双重图像文件加密算法步骤如下:
Step1:对图像文件进行改进的傅立叶变换加密
(1)首先对一幅原始图像IMG进行二维傅立叶变换,并提取出其幅值信息A和相位信息θ。
(2)与被授权接收图像的部门约定一幅与原始图像相同大小的均匀分布的矩阵图像作为密钥图像,对这个图像做二维傅立叶变换,提取出幅值信息F,用这个幅值信息F调制原始图像的相位信息θ得到加密后的相位信息φ,公式为:
φ=θ*F[2-3]。
(3)计算a*exp(jφ)的逆傅立叶变换得到B,完成图像文件加密过程。
Step2:对图像文件进行Fibonacci变换加密
(1)把step1的最终运行结果B做Z字型扫描重组成一维数组,在Fibonacci数列中选择一个比数组大小稍大一些的数作为Fn+1,例如,数组大小为1×10000,则可以选择Fn+1=10946,数组大小不匹配的最后946个采样点用0来填补,得到数组C。在Fibonacci数列中选择与Fn+1相邻的较小的数作为E。
(2)按照式(3)进行Fibonacci变换得到Sk(k=0,1,2,…,Fn+1-1),把一维数组C按照Sk的顺序重新排列得到D,D数组的值就是经过Fibonacci变换置乱后的信息,也是要在网络中传输的加密信息。
2、解密方法
当网络中传输的加密信息到达被授权的接收方时,需要对加密信息进行解密才能还原出原始图像被人读取。解密过程与加密过程相对应,分为两步进行,过程如下:
Step1: Fibonacci变换解密
(1)根据加密时所选择的Fn+1的值查出对应的周期N,把接收到的信息D’做N-I次Fibonacci变换得到C’,这时Fn+1的取值应该与加密时的取值相同。
(2)去除加密时在数组尾部添加的值为0的元素后,重新排列成二维矩阵B’,Fibonacci变换解密过程完成。
Step2:改进的傅立叶变换解密
(1)把B’进行傅立叶变换,提取其幅值信息A’和相位信息φ’,对与图像发送方约定好的密钥图像进行傅立叶变换,提取其幅值信息F’,计算θ’=φ’/F',得到还原了的相
位信息θ’。
(2)计算A’*exp(jθ’)的逆傅立叶变换得到IMG’,完成图像文件解密过程得到原始图像。
三、实验结果
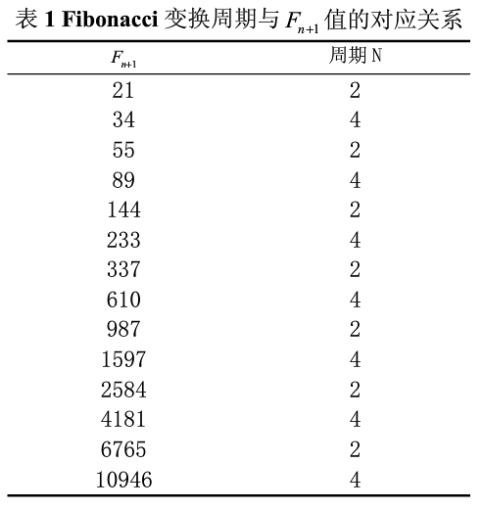
在图像文件双重加密算法的计算机模拟中,选择了大小为256×256的灰度图像作为原始图像,转换为一维数组后,数组的大小为1×65536。因此选择Fibonacci数列中的75025为Fn+1,那么比75025较小一些的Fibonacci数列中的数46368就是Fn的值。从表1中可以推出此时Fibonacci变换的周期N=4。
根据前面介绍的图像的双重加密算法原理,对这幅原始图像做了一系列变换运算之后,得出的实验结果如下:
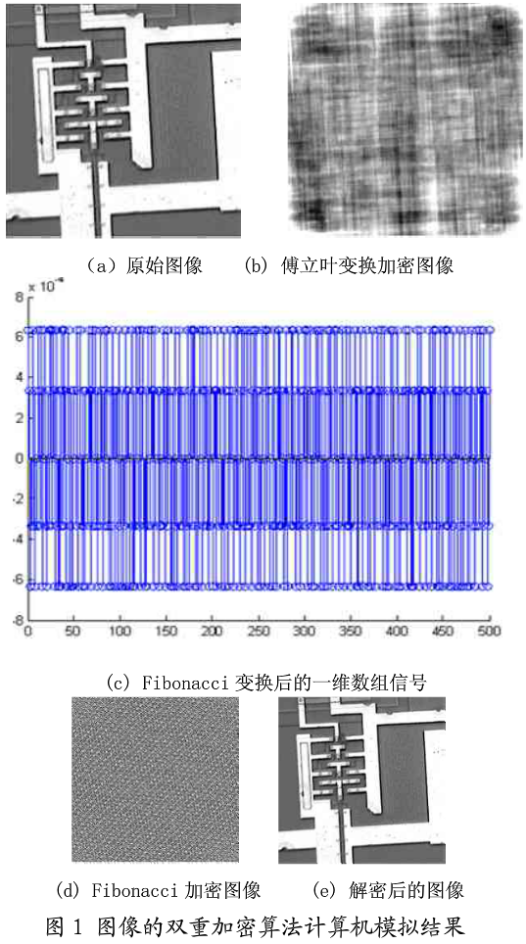
图1中,图(a)是待加密的原始图像,大小为256×256。图(b)是图像双重加密算法中的第一重加密一一傅立叶变换加密后的图像,加密过程中的密钥是由计算机随机产生的
均匀分布的大小为256×256的矩阵。图(c)显示了图像矩阵经过第一重加密后,矩阵排列成的一维数组经过Fibonacci变换后的置乱数组前500个元素值。可以看出,
数组经过Fibonacci置乱后,能量值呈均匀分布。图(d)显示的是图(c)排列成的矩阵的图像显示。图(e)是被授权的接收方最终解密得到的图像。
实验证明,该图像文件双重加密算法可以成功的实现图像文件的加密解密过程,并取得了较好的加密、解密效果和运行速度,双重加密也保证了加密算法的高安全性。
小知识之Fibonacci
又译费波拿契数、斐波那契数列、费氏数列、黄金分割数列。











