鉴于传统图像加密技术和低维混沌加密技术各自的局限性,将Lorenz混沌系统与数字图像置乱技术相结合,我们设计了一种基于三维混沌系统的数字图像加密算法。这种加密算法,首先,对系统输出的实数值混沌序列进行预处理;其次,以此实数值混沌序列直接构造图像置乱索引矩阵;最后,以8×8块为单位实现数字图像的空域加密。
一、Lorenz混沌序列及预处理
混沌之所以适合于数字信息文件加密,是因为混沌运动具有以下特征:(1)既非周期又不收敛,运动轨迹上的点遍历整个区域;(2)运动轨迹在有限区域内不断伸缩、折叠,使系统输出类似于随机噪声;(3)系统运动对初始值极为敏感,任意接近两点的长期运动不可预测。这些动力学特点使得混沌序列宽频带,类随机,难以破译:随初始值的不同能产生大量不相关的混沌序列,加密空间大;由确定性系统产生,使得混沌序列可控制可再生,为加密和解密提供了可能。
Lorenz系统是经典的三维混沌系统,以Lorenz系统生成加密混沌序列有三大优点:一是系统结构较低维系统复杂,系统变量的实数值序列更不可预测;二是对系统输出的实数值混沌序列
进行处理,可产生单变量或多变量组合的加密混沌序列,使得加密序列的设计非常灵活;三是系统的三个初始值和三个参数都可以作为生成加密混沌序列的种子密钥,若设计过程中再加入部分控制变量,图像加密算法的密钥空间将大大高于低维混沌系统。
Lorenz系统的动力学方程为:
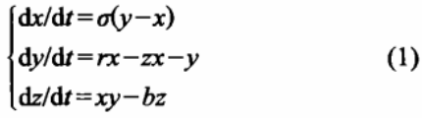
式中,σ,r,b为系统参数,典型值为σ=10,r=28,b=8/3。在保持σ、b不变,r>24.74时Lorenz系统进入混沌态。Lorenz三维系统需要用数值积分来求得实数值混沌序列,典型的数值积分法有一阶Eujer法和四阶Runge-Kutta法,前者计算量和计算精度远比后者低,但对图像置乱来说,考虑的是混沌序列类随机性所能达到的置乱程度,并不考虑混沌序列取值的精确度.所以本算法回归采用一阶Euler法,既不失Lorenz系统的混沌特性,又能提高算法的计算速度。
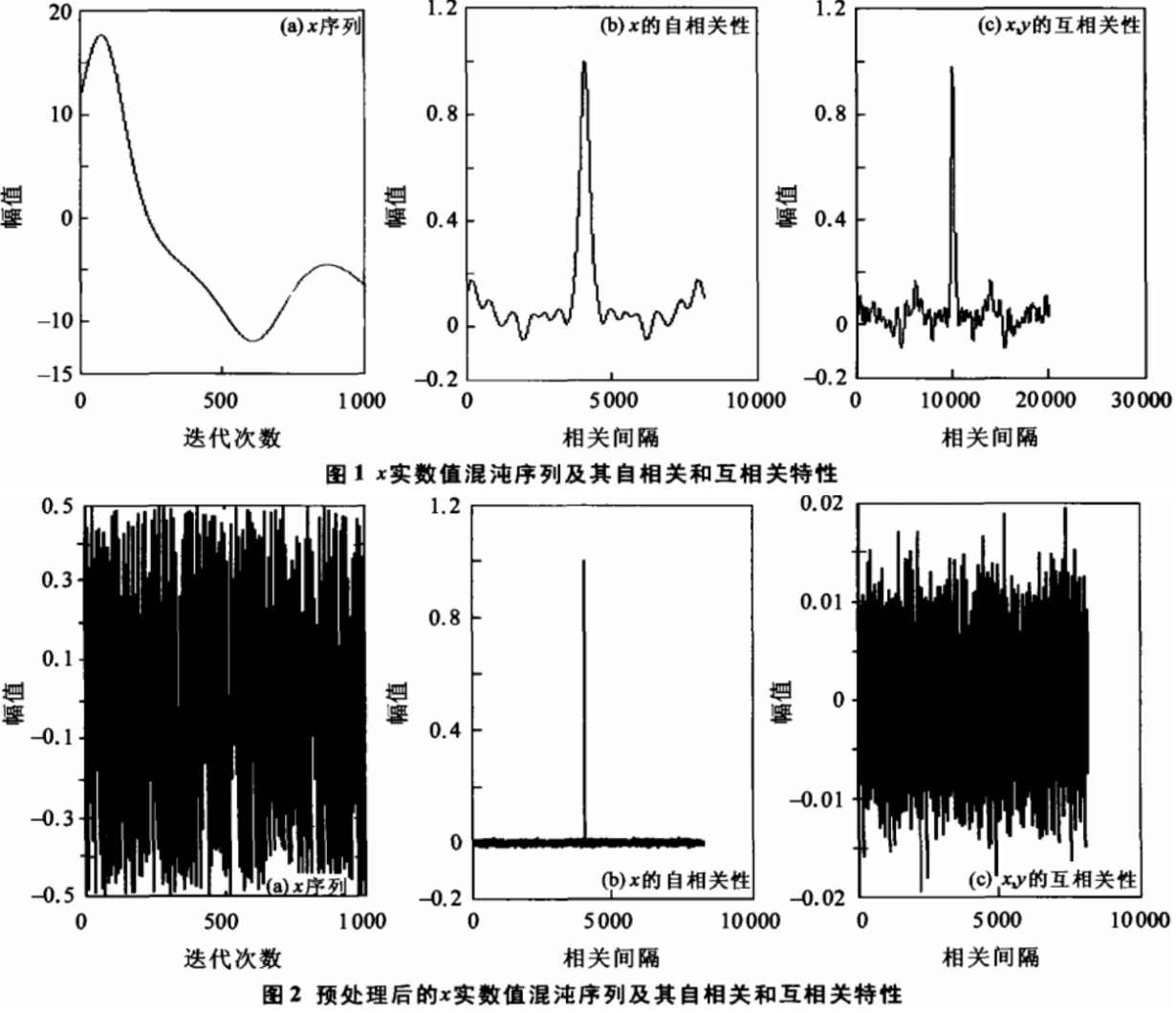
仅以x序列的特性为示例,如图1所示。系统初始值:xo=1.1840,yo= 1.3627,zo=1.2519。控制参数:σ=10,r=28,b=8/3。积分步长h=0.001,迭代次数n= 10的4次方;截取长度34000-35 000。按照Golomb对伪随机序列提出的三个公设,理想的混沌序列应具有的统计特性:均匀分布,自相关是δ函数,互相关是零。而在上述条件下,x,y,z实数值混沌序列值域分别为-20 <x<20,-28<y<28,0<z<50,不利于批处理;平均值分别为Vx= -1.9999,Vy= -2.008,Vz=24.066,均匀分布特性较差:局部取值呈现一定的单调性,容易被破译;自相关和互相关特性均不够理想,限制了序列的灵活使用。
通过近千组数据分析,对x,y,z实数值混沌序列需要做如下预处理:(1)去除各实数值的整数部分,统一值域;(2)为增强序列取值的无规则性及整体分布的均匀性,在去整的基础上再将小数点后移数位。整个预处理过程可由下式实现:
![]()
式中,round(.)为取最接近整数运算。
图2是预处理后工实数值混沌序列及自相关特性和与y序列的互相关性,预处理结果:x,y,z列的值域为(-0.5,0.5):平均值Vx=-0.001 3897,Vy=-0.000 903 0,Vz=0.0008211,基本接近于零;自相关Rrmax=0.0126,Rrmay=0.013 1,Rrmaz=0.0094,即自相关特性是较理想的6函数;互相关最大偏差Rcxmax= 0.0147,Rcymax=0.0 11 9,Rczmax 0.012 1,即互相关特性近似为零特性;x,y,z序列取值更加无规则。比较图1和图2可以直观地看出,预处理后的混沌序列具有良好的均匀分布特性、随机统计特性和相关特性。
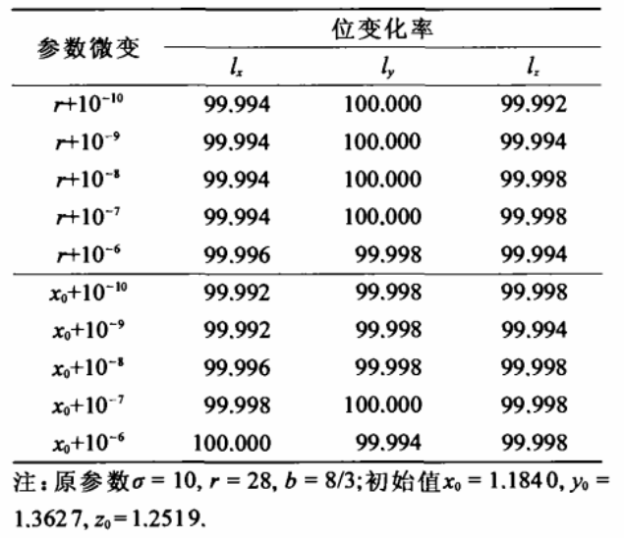
本文还对预处理后的x,y,z实数值混沌序列对初始值和系统参数敏感性做了测试。表1给出了以系统参数r和初始值x0而发生微小变化为例的测试结果,其中的位变化率指索引序列(定义在后)的位变化率。可以看出,当系统参数r和初始值xo发生10的-10次方微小变化时,除去序列的初始段,索引序列的位变化率达100%。
结果表明;预处理后的x,y,z序列有着更强的伪随机特性,用于图像置乱将会有更好的置乱效果;良好的相关特性使x,y,z三序列可独立地构成三个单变量加密混沌序列,也可多变量组合构成多个加密混沌序列,有望实现图像的多路并行加密;对系统参数和初始值极强的敏感性说明,除非确切知道密钥,否则很难进行有效的解密。理论上本算法密钥空间为无穷大,可以很方便地构成一次一密的密钥体制。由此说明预处理过程是正确可行的。
二、图像加密算法和解密算法
本文基于图像空间几何置乱的机理,利用Lorenz系统的混沌序列来构造置乱规则矩阵P,在此称为置乱索引矩阵。
(1)定义P,其任一元素Pij∈_{1,2.…,l),且Pij=Pkl,当且仅当i=j,k=l;
(2)按需要长度,随机截取预处理后的x,y,z实数值混沌序列,然后按升序排列,[x,lx]=sort(x)[y,ly]=sort(y),[z,lz]sort(z);
(3)索引序列lx,ly,lz即用来构造置乱索引矩阵Px,Py,Pz。索引序列指定Px,Py,Pz中各元素的几何位置,各元素按索引序列的顺序赋为1-l的自然数。
为提高图像文件加密效率,不破坏图像压缩效果,将图像进行8x8分块,以块为单位对图像进行全局置乱变换。因为JPEG是以8x8的图像块为基本单位进行编码的,所以这样做不影响块的DCT系数的分布,使得Huffman编码表能按最优方式使用,因此该图像加密算法能抵抗图像压缩攻击。这样整个加密算法的步骤如下:
(1)输入原始图像,预处理:边界填充0(黑色),使图像大小为8x8块的整数倍。
(2)构造置乱索引矩阵,输入密钥(σ,r,b;x0,yo,zo),生成实数值混沌序列{xi;i=1,2,3,...},{yi;i=1,2,3,...},{zi;i=1,2,3,...},对x,y,z实数值混沌序列进行预处理;按需要长度l= (MxN)/(8x8)随机截取实数值混沌序列,生成索引序列{lx;i=1,2,3,...},{ly;i=1,2,3,...},{lz;i=1,2,3,...};构造置乱索引矩阵Px,Py,Pz。
(3)图像置乱。以块为单位,按置乱索引矩阵规则,重排图像各块的几何位置。
解密算法是上述加密算法的逆过程。
从结构上来说,整个图像加密算法主要由三部分组成,一是对实数值混沌序列的预处理,二是构造置乱索引矩阵,三是以块为单位的空域全局置乱。这里韵关键是对x,y,z实数值混沌序列进行预处理,使其具有更强的伪随机特性,以加强置乱索引矩阵的随机性,从而提高图像置乱程度和算法的破译难度:Lorcnz混沌系统对系统参数和初始值高度敏感性,使得算法的密钥空间非常大,使加密者可以随意地选择密钥,这样的选择可以使算法有着几乎一次一密的安全特性。
三、仿真
选择具有不同纹理特征,大小均为512x512的Lena, Peppcrs,Plane三幅标准图像作为仿真对象,如图3所示。

选择密钥觑参数σ=10,r=28,b=8/3。初始值x0= 1.1840,yo=1.3627,zo=1.2519。分别用x,y,z实数值混沌序列对三幅图像文件进行加密,结果如图4所示。

图5是以Lcna图像为例的正确解密图像和错误解密图像,错误解密图像分别对应参数r有10-10偏差和初值xo有10-1o偏差时的错误解密,如果要采取唯密文攻击的话,要三幅图像都正确解密,则要搜索的密钥量高达3x40961。如果图像更大,可以说算法能够抵抗唯密文攻击,对选择明文的攻击也有较高的安全性。

数字图像在传输过程中,很难避免一些必要的数据处理或人为攻击,如压缩、滤波、噪声污染及几何失真等.对一些比较常见的处理和攻击,本文也进行了仿真测试,测试结果以图6示之,其中三图分别是以Lena为例的加密图像经JPEG压缩后的解密图像,以Peppers为例的加密图像受到IO%的高斯噪声污染后的解密图像,以Planc为例的加密图像经破坏性的无规则剪切后的解密图像,仿真结果表明,该图像加密算法具有可行性、可靠性以及抗攻击和抗干扰能力。

小知识之动力学
动力学是理论力学的一个分支学科,它主要研究作用于物体的力与物体运动的关系。动力学的研究对象是运动速度远小于光速的宏观物体。动力学是物理学和天文学的基础,也是许多工程学科的基础。许多数学上的进展也常与解决动力学问题有关,所以数学家对动力学有着浓厚的兴趣。









