为了能对经过剪切变换攻击的加密图像文件进行有效恢复,我们给出了一种基于混沌序列的数字图像加密算法,该方法在预处理的基础上,基于文字图像文件灰度矩阵位平面进行置乱加密,在恢复过程中通过像素邻域灰度信息进行恢复,能够有效抵御针对加密图像文件的剪切变换攻击,下面我就给大家详细的介绍一下这种图像加密算法。
一、抗剪切变换攻击数字图像加密算法原理及其改进
数字图像文件(Image) 一般由相应的灰度直方图表示,无论是利用位置置乱还是灰度变换的方法加密图像文件,都是要改变图像像素(Pixel)的灰度值。现在常用的基于混沌系统的图像加密算法均是将像素位置置乱与灰度变换相结合来实现对灰度图像文件加密。本文在此基础上,将图像加密算法表示如下:
Step1、输入待加密图像Image,对应的灰度矩阵记为I,将灰度矩阵中的像素灰度值表示成二进制序列,相应的三维二值矩阵记为B。
Step2、利用混沌系统生成混沌序列,将其转换成与B相同大小的二值矩阵A。
Step3、对图像进行预处理,计算AXORB,结果记为C,将C的8个位平面分别记为C1,C2,…,C8。
Step4、利用混沌系统生成8个魔方变换矩阵,分别对C1,C2,…,C8进行魔方变换,得到的结果分别记为E1,E2,…,E8。将其对应的三维二值矩阵记为E。
Step5、将矩阵E进行十进制转换,得到加密图像的灰度矩阵E1,所对应图像即为加密图像Eimage。
解密过程是上述加密的逆过程。对于遭受到剪切攻击的图像,在恢复过程中,由于待解密图像的灰度矩阵不完整,为此,我们在恢复过程中对待解密图像的三维二值矩阵的缺省部分给出标记,在利用逆魔方变换矩阵进行计算后,每一个位平面将有部分位置上的0,1值缺省,而且根据混沌序列的伪随机性可知,缺省位置将均匀分布于每一个位平面上,基于以上分析,我们对每一个位平面均应用以下方法进行处理:如果当前位置恢复出了0.1值,则将其保留作为当前位置的值:如果当前位置没有恢复出0,1的值,则考虑其周围4——邻域相邻位置的0,1值,取当前位置的值与邻域值中0,1分布的概率较大的值相同.当出现当前位置与周围4——邻域位置均没有恢复出0,1值时,我们再取当前位置的8邻域范围继续以上过程,以此类推,直到当前位置取到值为止。根据该方法,可以恢复出图像三维二值矩阵所有位置上的0,1值,从而得到解密图像。
以下是直接应用以上加密方法进行图像文件加密和剪切交换攻击的实验结果。

通过实验结果可以看出,该方法对于剪切变换攻击基本能够恢复出原图像的信息,但是恢复的效果较差,恢复图像中含有类似于噪音的不连续的像素,从而影响了图像的恢复效果。为此,我们对恢复图像应用3x3模板的中值(Mtdian)滤波器进行去噪处理,然后应用线性锐化滤波器对图像进行锐化处理,得到的结果图像即作为最终的解密恢复图像。
二、混沌二值序列生成方法
以上图像加密算法中,我们以一维的Logistic混沌系统为例,来具体说明二值混沌序列的生成方法,Logistic混沌系统表述为:
![]()
其中当3.571448<μ<4时,该混沌映射处于混沌状态,把3.571448q<4称为混沌区域,a0∈(0,1),这样Logistic映射可以定义在(0.1)上,相应得到定义在(0,1)上的伪随机序列{ak}k∞=o。
设由混沌系统生成的混沌侍:列记为:{a1,a2....an|,ai∈(o,1)i=1,2,…,n},现在要对其进行二值化,设相应得到的二值序列记为{b1,b2....bn|,bi∈(o,1)i=1,2,…,n}
基本的混沌序列二值化方法,该方法的基本思路是;根据混沌序列{a1,a2....an|,ai∈(o,1)i=1,2,…,n},定义相应的二值序列{b1,b2....bn}为:
![]()
则bi∈(o,1)i=1,2,…,n。利用方法得到的二值序列具有良好的伪随机性,但是该方法是线性离散化的方法,安全性较差。
我们在此方法的基础上,给出改进的基于混沌序列的二值序列生成方法,该方法的基本思想是:根据混沌序列{a1,a2....an|,ai∈(o,1)i=1,2,…,n},定义相应的二值序列{b1,b2....bn}为:
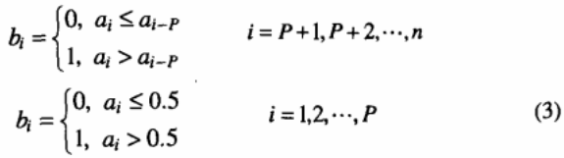
其中1<P<n,则根据以上方法可以得到相应的二值序列bi∈(o,1)i=1,2,…,n。与已有的混沌序列二值化方法比较,本文所给方法在比较过程中增加了步长参数P,扩大了生成二值混沌序列的密钥空间,同时这种错位比较的方法与前面所用方法的线性方法比较,能有效增加算法的安全性。
以下通过实验对以上两种方法进行比较。为了检验本文所给的混沌序列非线性离散化方法生成的二值混沌序列的随机性和对初始条件的敏感性,我们以典型的Logisric混沌系统为例,通过实验与已有的方法的实验结果进行比较分析。
根据Golomb的随机性公设,为了保证伪随机序列具有尽可能好的随机性能,我们对生成的二值序列的随机性进行以下检测:
1)频数检验,保证序列中0和1的个数大致相等,这也是二值序列具有随机性的最基本保证。计算:
![]()
其中伽为二值序列中0的个数,n1为二值序列中1的个数,与l自由度的X12分布比较,对应5%的显著水平,X12的值为3.84,只要得到的值不大于3.84,则认为序列具有较好的随机性。
2)序列检验,我们对所得到的二值序列内00、01、10、11(二维均匀性)出现次数进行统计,同时计算:
![]()
其中nij,i,j∈(0,1)表示二值序列中“ij“的个数,对2自由度的X22分布比较,对应5%的显著水平,X22的值为5.99,只要得到的值不大于5.99,则认为序列具有较好的随机性。
1、混沌二值序列的随机性分析
为了保证伪随机序列具有尽可能好的随机性能,我们对生成的二值序列的随机性进行检验:
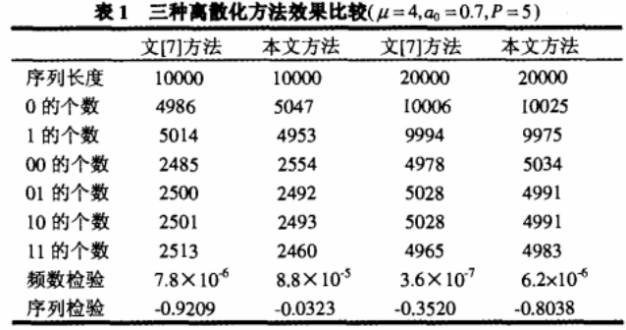
通过表l的实验结果可以看出,本文所给出的基于混沌序列的离散化方法得到的二值序列中0和1的个数、统计的二值序列内00、01、10、11(二维均匀性)出现次数均基本相当,通过频数检验和序列检验,说明所得到的二值序列具有很好的随机性。
2、混沌二值序列的初值敏感性分析
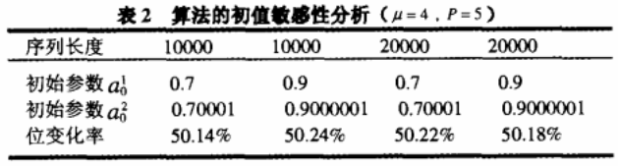
好的混沌序列应该具备对初始条件的敏感性,这是所有混沌系统的内在性质,在检验过程中我们对混沌系统的初始条件进行微小变化,通过统计所得到的二值序列中相应位置上的0和1的值的变化情况,位变化率越接近50%,说明该系统对于初始条件越敏感。
通过表2的实验结果可知,该离散化方法具有对混沌系统初始条件的敏感性,因为当初始值发生微小的变化时,所生成的二值序列中仍有近半数的位的0和1的值发生了变化,很接近理想的混沌系统对初始条件的敏感性要求。
三、魔方变换矩阵生成方法
我们仍然以一维的Logistic混沌系统为例,来具体说明魔方变换矩阵的生成方法。本文给出了一种基于一维混沌系统的魔方变换矩阵生成方法,具体过程如下:
设待加密的图像文件为Image,大小为m×n,魔方矩阵通过一维Logistic混沌映射产生一维混沌序列,将生成的实数混沌序列映射到整数范围Xn∈[1,m×n],具体方法是:
![]()
根据以上方法,给出混沌系统的初始条件x0和μ,可以得到相应的整数序列,在该整数序列中选择Xh,Xh+1,…,其中Xh表示序列中以前还未出现的整数值,同时删除所选序列中重复出现的整数,得到mxn个整数,将这些整数按行排列得到相应的魔方变换的矩阵Pmxn。
下面分析以上产生魔方变换矩阵的方法,要得到Pmxn,必须首先得到{1,2,…,mxn}上的一个完整的排列。
当mxn的值较小时,要得到{1,2,…,mxn}上的一个完整的排列,要求生成的混沌序列的长度越长越好,因为较小的小×几使得邻近的不同实数序列值对应相同的整数的可能性增大。反之,如果mxn的值较大,则通过计算机实现时,由于计算机的有限精度效应,混沌序列必然退化为周期序列,从而使得相应生成的整数序列(X1,X2.…)必然也退化成周期序列,如果该整数序列的周期小于m×n,则通过以上方法不可能得到魔方变换矩阵。我们以使用的Logistic映射为例,通过实验分析来说明该问题。
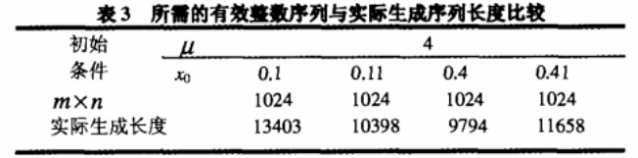
通过实验分析可知,需要生成的序列长度远远小于要生成满足需要的序列而实际生成的混沌序列的长度,使得图像加密算法的效率大大降低。
针对以上分析,我们给出一种改进的得到魔方变换矩阵的方法,根据图像大小mxn生成相同大小的混沌序列X1,X2,…,Xm×n。xi∈(o.1),i=1,2.…,mxn,对生成的混沌序列按大
小进行排序,将得到的结果序列记为{Xs1,Xs2,…,Xsm×n},其中s(i)∈(1,2.…,mxn),则新序列的下标构成序列{1,2.…,mxn}的一个排列,将该排列按行重排即可得到相应的魔方交换矩阵Pmxn.该方法的优点是根据待加密的图像文件来生成相同大小的混沌序列,无需多余的计算,此外该方法也不需要考虑应用计算机实现时存在的序列周期问题。以下是
对一维混沌系统的魔方变换矩阵和本文给出的改进的魔方变换矩阵生成方法的实验比较,在相同的混沌系统和初始条件的基础上,生成相同长度的魔方变换矩阵对应的整数序列,通过比较两种方法的运行时间对效率进行比较。
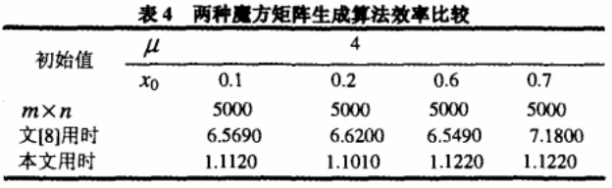
通过实验比较可知,改进方法与原有算法比较,生成相同大小的魔方变换矩阵所需要的运行时间大大降低了,从而实现了图像加密算法效率的提高。

四、实验结果
图2是应用本文所给图像加密算法的实验结果。
实验结果表明,该图像文件加密方法能够很好地抵御剪切变换攻击,当剪切面积小于50%时,恢复出的图像效果较好,当剪切面积大于50%时,图像的细节信息很难恢复,整体的恢复效果较差。
小知识之剪切变换
剪切变换——又称“错切变换”,是仿射变换的一种原始变换,指的是类似于四边形不稳定性那种性质,方形变平行四边形,任意一边都可以被拉长的过程。











