admin 根据排列与图像置乱之间的关系，利用混沌映射，提出一种新的生成排列的方法，并由此得到图像置乱所需的行置乱矩阵和列置乱矩阵，实现了图像文件的循环迭代加密。通过一系列图像置乱效果评价指标的测试，表明该加密算法操作简单，具有较高的执行效率，且有良好的置乱效果以及良好的安全性。
一、加密算法原理
对于大小为M×N的图像AM×N，由于任一置换p都可以分解为若干个互不相交的轮换之积如果直接得到{1，2，3，…，M×N}上的全排列，则面临易被分解为轮换之积继而解密出图像文件的问题。因此较好的做法是对原图像文件分别进行行置换和列置换操作。由于图像具有M行N列，在行置换时，对应于每一行，均生成{1，2，3，…，N}上的排列，进行M次合并后得到“行置换矩阵”。同理，在列置换时，对应于每一列，均生成{1，2，3，…，M}上的排列，进行N次得到“列置换矩阵’’。为了得到行（列）置换矩阵需要生成给定集合上的排列。考虑到加密图像文件的安全传输以及正确解密，因此希望生成排列的算法尽可能简单，并且传输该算法的参数个数尽可能少。目前，能够满足这些要求来生成排列变换的一种技术是使用混沌映射。
混沌现象是一种非线性动力系统中出现的类随机过程，该过程是非周期的并且对初值具有很强的依赖性生成的随机序列具有良好的伪随机性。最早将混沌系统理论应用于加密算法的是M atthews，由于混沌系统具有优良的统计特性以及不可预测性所以近年来被广泛应用于图像文件加密和数字通信领域。本文根据置换群的性厩利用一维混沌系统，给出一种将实数混沌序列转化为给定集合上整数排列的简单方法以实现对图像文件的置乱加密。具体做法是利用混沌系统生成实值序列，为了保证序列的随机性，舍弃起始的序列，从中间某一位置开始取长度为2×M×N的随机序列，进行扩大取整前M×N个随机整数用于生成行置换矩阵，后M×N个随机整数用于生成列置换矩阵，并转化为与原图像大小相同的矩阵形式，称之为行与列随机矩阵。
首先考虑生成行置换矩阵，记原图像矩阵每一行的N个数顺序排列时的下标为对应像素点的原始位置，即图像每一行像素的原始位置为{1，2，3，…，N}。对行随机矩阵而言，每一行均有N个随机整数，本文提出的将N个随机整数转化为1到N的一个排列的方法为：从第二个数开始将该随机数与其之前的所有随机数逐一进行模N比较，一旦该数之前的随机数中存在与该数模Ⅳ后相同的随机数，则对该随机数执行加1操作，再重新与其之前的随机数进行模N比较，反复进行，直到得到N个模N后互不相同的数，用模N后的值代替原有的值，即得到一个1到N的完整排列。对M行采用相同的方法进行处理可以得到行置换矩阵。图像行置换的方法是将原图像矩阵每一行的所有像素点移至行置换矩阵中该行对应位置表示的位置处。例如，若图像的列值为5，与行置换矩阵相结合，图像某一行在行置换矩陈，电的对应须为[3，5，2，1，4]，则该行变化前后的关系为：
，表示将原图像中该行的第1位移至第3位第2位移至第5位，以此类推，完成对图像的行置乱加密。同理对列随机矩阵的每一列进行模M处理，得到列置换矩阵。将列置换矩阵与图像矩阵相结合，按相同的方法对图像像素点进行移动，以实现对图像文件的列置乱加密。
这样生成排列的好处在于：只需对与图像大小相同的随机序列进行处理并且一旦得到置换矩阵便可以很方便的对图像文件进行迭代加密，以得到更好的加密效果。图像加密算法过程如下：
1、原图像的加密算法
Step1：输入原图像及混沌系统的初值，根据混沌映鼽得到随机实数序列，对序列进行放大取整得到行与列随机矩阵。
Step2：将行随机矩阵每一行的Ⅳ个随机整数变换为1到N的一个完整排列，进行M次，得到行置换矩阵。同理，将列随机矩阵每一列的M个随机整数变换为1到M的一个完整排列，进行N次得到列置换矩阵。
Step3：将待加密的图像矩阵与行置换矩阵相结合，得到行加密后的结果图像。再与列置换矩阵相结合，得到经过行与列加密后的加密图像文件。
Step4：完成一次迭代循环次数加1，判断是否达到加密效果，如果满足则终止程序，否则返回Step3。
2、加密结果图像解密算法的实现
利用接收到的密钥，重构出行与列置换矩阵，将加密图像文件矩阵与置换矩阵进行逆向运算，即可以获得解密的结果图像文件。
根据加密算法的设计思想一旦得到行与列置换矩阵，那么在图像文件迭代加密过程中，置换矩阵并不改变，即利用同一个行与列置换矩阵对图像文件进行循环迭代加密。加密算法中迭代次数的选择是根据我们对图像文件加密效果的要求而定的，而加密效果的评定是通过对实验运行的结果图像进行主观评价，可以根据自己的要求设置迭代次数。
二、实验结果
实验部分采用表达简洁、计算方便的Logistic混沌系统，生成实数序列，Logistic映射定义为：
其中初值a0∈（0，1），参数μ∈（0，4]，当3. 569946…≤μ≤4时，Logistic系统处于混沌状态。当给定初值ao、参数μ后，根据(1)，可以得到混沌实数序列，对生成的实数序列进行放大取整，得到整数序列，进行处理后生成行与列置换矩阵，对原图像首先进行行置挽再对行置换图像进行列置挽完成一次加密，迭代次数加1。
对大小为256×256的lena图像迭代加密3次，图1分别给出了原图像、加密后的结果图像、正确解密的结果图像和不能正确解密的结果图像。
其中加密图像时混沌系统的初值为随机生成的0. 6154，参数为4.0，而当初值有0.0000001的改变时，便不能对加密图像进行正确的解密，表明本加密算法对初值具有极高的敏感性以及较高的安全性。
图2给出对图1的lena图像用本方法进行迭代加密的结果图像。
其中加密图像时混沌系统的初值为随机生成的0. 4565，参数为4.0，可以直观的看出随着加密次数的增大，加密结果图像越来越好。采用先行后列的置乱方式，可以使任一个像素点遍历整幅图像，以达到更好的加密效果。
三、加密算法分析
为了对文中提出图像加密算法的性能进行分析，对像素个数为124× 124的图像，随机选取20个初值，迭代加密5次后，对每一次的结果图像进行分析得到以下统计数据。
1、 不动点分析
本图像加密算法在加密图像文件时，只是像素点位置的变化，像素点的灰度值并没有发生变化。不动点分析主要是统计图像加密前后图像像素点中相对位置没有发生改变的个数。不动点越少，表示图像的加密效果越好，加密算法的性能越好。表1给出了124×124加密结果图像中不动点占总像素点比例的统计结果。由表1可知，用本加密算法得到的结果图像中，不动点个数占整幅图像像素点个数的比例为0. 64 -0. 92，表明了图像的像素点基本都发生了位移，加密算法具有较好的置乱效果。
2、移动平均距离分析
本图像加密算法的加密思路是对图像先进行行置换加密，再进行列置换加密，移动平均距离的分析是对加密前后图像中所有像素点移动的距离进行统计平均。为了方便统让考虑到行置换时，各个像素点只是在本行进行移动，纵向位移为0，在列置换时，各个像素点的横向位移为0。所以先分别统计出行与列置换时所有像素点移动的总距离分别为S1和S2，则移动平均距离为
。图像像素点的移动平均距离反映了像素点总体的位移情形，移动的平均距离越大，得到加密结果图像中各个像素点的相关性越差算法的置乱性能越高。表2给出了124×124加密结果图像中所有像素点移动平均距离的统计结果。
由表2知，加密结果图像的移动平均距离为40. 7676- 41. 3450，移动平均距离的平均值为410846，基本上与随机置乱移动的平均值124/3≈41. 333相符，表明了加密算法具有较好的性能。
3、自然序分析
对自然序进行分析是考虑图像在加密前后与其周围像素点的相关性能，即若原图像虽然经过置乱加密，但不排除在原图像中相邻的像素点在置乱加密的结果图像中依然处于相邻的位置，这种情形称为自然序。如果加密的结果图像中存在过多的自然序，则使得加密图像不能很好的隐藏原图像中的信息。所以自然序的数目越少，加密算法的性能越好。表3和表4给出分别用原图像中2×2与3×3的分块对加密图像中的自然序进行统计的结果。
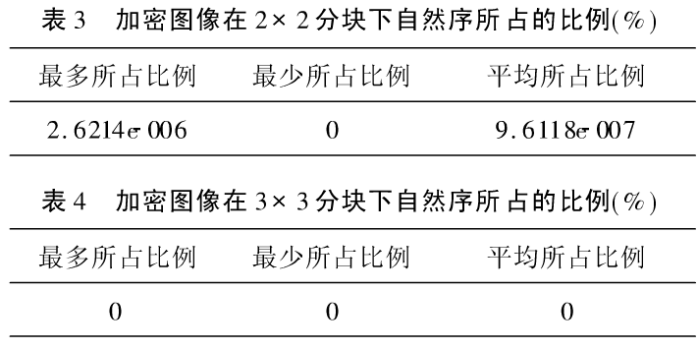
由表3和表4知当分别采用原图像中所有的2×2和3×3的分块测试加密结果图像的自然序占图像中全部分块的比例时，对2×2分块而言，自然序平均所占的比例为9. 6118e—007，这个数已经相当的小。而当用3×3的分块时，所有的情形均为0，表示加密图像中任意3×3的分块或者大于3×3的分块中已经没有和原图像中相同的像素点，它们被置乱至图像的其它位置，所以本算法可以使像素点遍历整幅图像，具有良好的置乱性能。
4、汉明相关性分析
汉明相关性分析主要是对加密结果图像的任意一行（列）与其它各行（列）的相关性进行分析。对任意两个序列x= {x1，x2，x3，...，Xn}与y= {y1，y2，y3，...，yn），它们的汉明相关定义为：
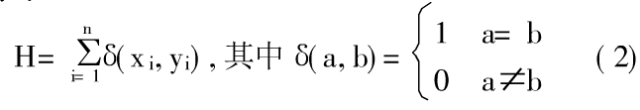
统计任意行（列）的所有元素与其它各行（列）相应位置具有相同元素的概率，汉明值越大则相关性越强，算法的置乱性能就越差。表5和表6分别给出了对加密图像的任意一行（列）与其它各行（列）在相同位置具有相同元素的个数的统计结果。
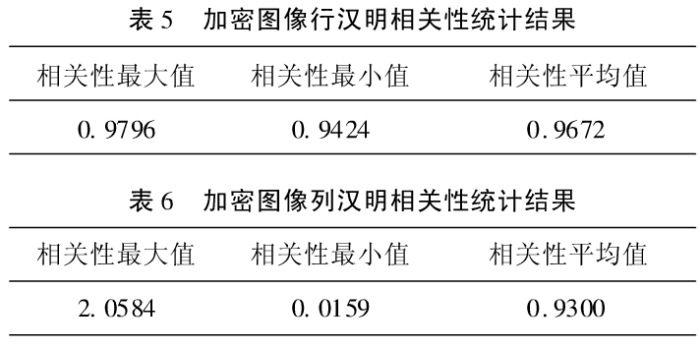
由表5和表6的行（列）汉明相关性平均值知，对加密图像的行与列而言，其任意一行（列）的所有元素与其它行（列）的所有元素在相应位置上有不到一个相同的像素值。
小知识之不动点
不动点，是一个函数术语，在数学中是指“被这个函数映射到其自身一个点”。
