基于二维可逆映射的图像加密算法可以通过置乱图像像素位置实现图像文件加密。二维可逆映射可以高效地实现网像像素置乱。二维可逆映射由压缩拉仲和折叠两个子映射组成。压缩拉仲映射,使原始图像变换成线,折叠映射使线变换成罔。所有可逆映射构成了可逆映射集合。经过扩散处理改变像素值,实现图像文件加密。
一、二维可逆映射原理和加密算法
二维可逆映射利用了图像的一个重要性质:像素能通过插入到其他像素之间从而压缩为线。设图像大小为M×N。通过映射首先将原图像压缩拉伸为长MN的直线,然后再折叠成一个M×N的图像。
如图1所示。(a)为上下压缩对角线折叠映射,(b)为左右压缩涡卷折叠映射。

设图像大小为M×N,设A(i,j),i=1,2,…,N;j=1,2,…,M为图像中的任意一点,l(i),i=1,…,MN为将A(i,j)拉伸后的向量,B(i,j),i=l,2,…,N;j=1,2,…,M为折叠后生成的密图坐标为(i,j)的像索点。[x]是取最接近于X的整数。
1、压缩算法
本文只在水平和垂直两个方向推导了压缩算法,分别为上下压缩映射和左右压缩映射。
(1)上下压缩算法
如图1(a)所示,上下压缩映射算法如下:
首先定义函数:
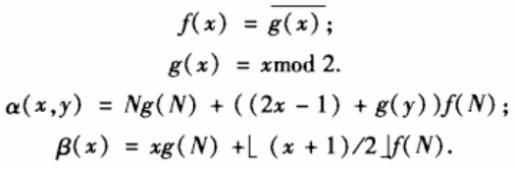
则上下压缩算法为:
![]()
其中:
![]()
其中:
![]()
(2)左右压缩算法
该压缩算法无论形式还是推导过程都与上一种类似。
如图1所示,左右压缩映射算法如下:
首先定义函数:
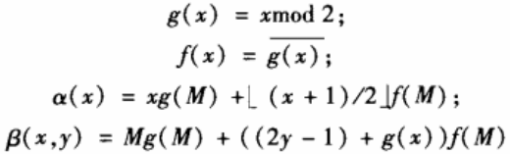
则左右压缩算法为:
![]()
其中:
![]()
其中:
![]()
2、折叠算法
推导了两类折叠算法,分别是对角线折叠和涡卷折叠。
其中每一种根据不同的起点又有四种变换,这样一共是12种折叠算法。四处起点分别为:左上、右上、左下和右下。本文只对两类算法在左上起点处给出了数学公式。
(1)对角线折叠算法
如图1(a)所示,对角线折叠算法如下:
![]()
其中:
![]()
其中:
![]()
其中:
![]()
式中,lmin表示M和N中的较小值,lmin表示M和N中的较大值。
(2)涡卷折叠算法
如图1(b)所示,涡卷折叠算法如下:
定义函数:
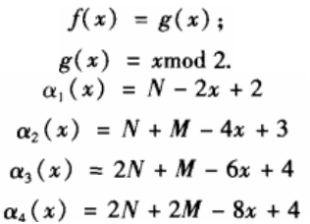
则涡卷折叠算法为:
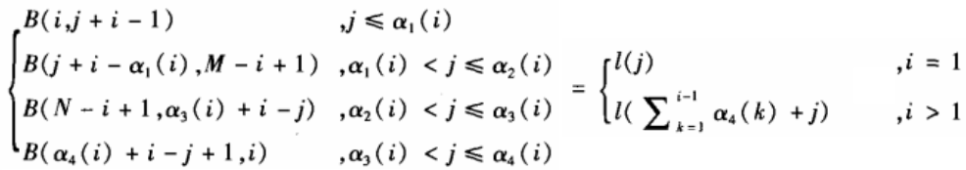
其中:
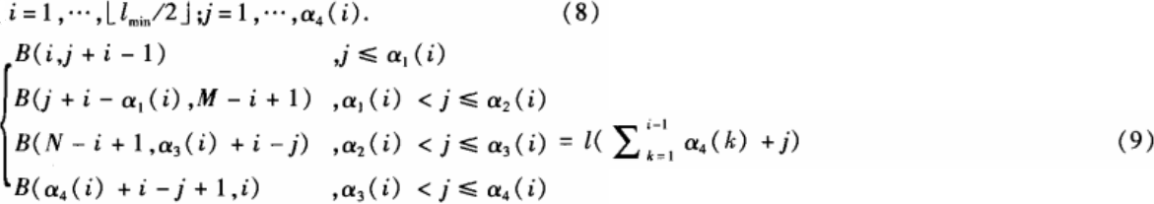
其中:
![]()
式中,lmin表示M和N中的较小值,lmin表示M和N中的较大值。
3、二维可逆映射集
上面介绍了两种压缩算法:上下压缩和左右压缩;两类折叠算法:对角线折叠和涡卷折叠;而每类折叠依据起点不同又分为四种,即折叠算法一共有2×4=8种。将压缩和折叠组合成可逆映射,则一共有2×8 =16种映射。将16种映射用A,B.…,O,P表示,其构成二维可逆映射集,用Z表示。即:
![]()
见表1所示:

如E表示上下压缩和左上起点涡卷折叠组合的二维可逆映射。
二、使用二维可逆映射实现图像的加密和解密密钥设计
由于各种映射构成了二维可逆映射集。将子映射种类和映射次数设计为密钥Keyo如Key;A1F2K3P4,表示图像依次A映射1次,F映射2次,然后用K映射3次,最后用P映射4次。其中A.F、K和P所代表的映射种类可查阅表1。为了保证加密效果,每一个部分密钥值都小于10。
加密算法如图2所示:
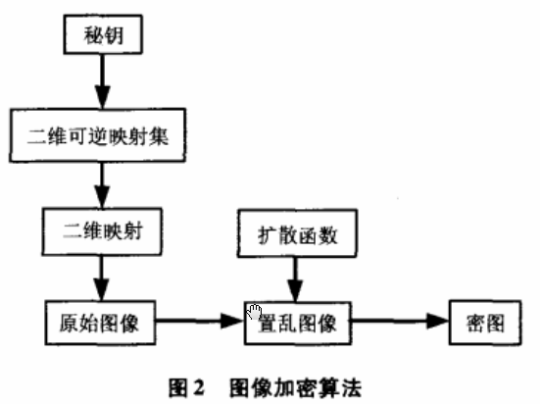
图像加密算法所采用的扩散函数为:
![]()
式中,A(i,j)是指扩散前每一个像素的值,A’(i,j)为扩散后的像素值,256灰度图L= 256。
图像加密算法分为三步:
1)利用密钥及公式(1)一(4)。将图像A(i,j)拉仲成一条直线l(i),i=0,1,…,MN -1。
2)利用公式(6)一(9),将直线折叠,得到置乱图像C(i,j)。
3)利用扩散函数,对置乱图像进行处理得到密图。
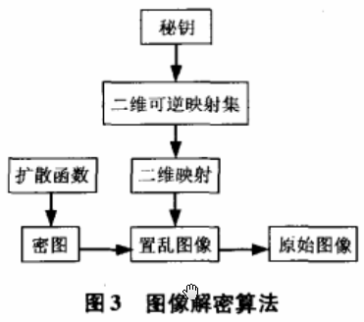
如图3所示,图像解密算法与加密算法相反,解密过程与加密过程对称,且解密密钥与加密密钥相同。
三、加密实例和安全性分析
通过运行仿真程序,得到了较好的加密结果;仿真结果表明该方法安全性较好。
1、运用二维可逆映射加密实例
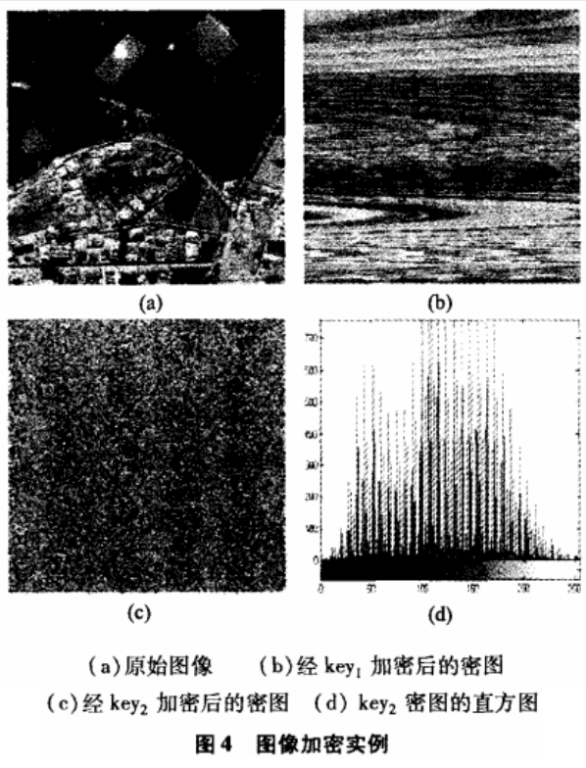
如图4所示,对256灰度图文件加密。为了研究二维可逆映射的加密效果,没有加入扩散函数。此时,加密系统仅仅置乱图像,没有改变图像的像素值(直方图不变),如图4(d)。如图4(b)所示当Keyi=A1时,图像已没有原图 特征。
如图4(c)所示当Key2=AIM2C3P4F5J6H7L8时,密图像素平均分布,加密效果良好。
2、安全性能分析
密钥空间分析
由于最基本、最流行的破解方法是对密钥进行穷尽搜索。密钥空间大是加密算法安全的前提。加密算法的密钥空间如表2所示。研究表明,密钥空间大小只和密钥长度有关,在理想情况下(计算速度允许),可认为密钥能无限增加。

密钥敏感度
当加密密钥Key=AIM2C3P4F5J6H71J8加密时,用解密密钥Key1=AIM2C3P4F5J6H7K8和Key2=AIM2C3P4F5J6H7 L9分别解密。如图5所示,即使加密密钥和解密密钥仅一位有最小的差异,也无法解密图像,证明对密钥差异非常敏感。

相关性统计分析
由于原始图像相邻像索之问具有很强的相关性,而二维可逆映射置乱像素后,一个很重要的特性就是改变了原来相邻像索间的联系。如果加密图相邻像素之间相关性变小,说明密图安全性变强。
用下列两个公式计算他们的相关系数:
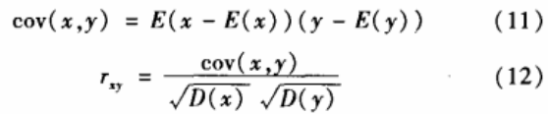
式中x、y为两个相邻点的灰度值。
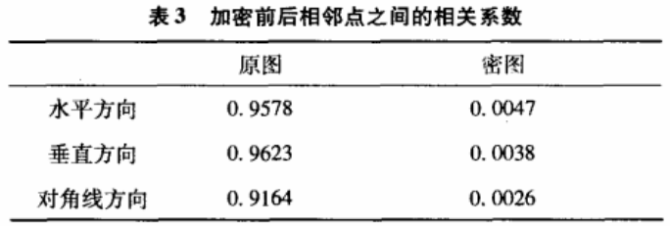
原图的相关系数为0. 9578.加密之后的相关系数为0.0047,证明密图相邻像素之间相关度接近于零。相邻点的相关系数如表3所示,说明密图相邻像素之间相关性很小。
3、扩散算法
仅对图像进行置乱,而不改变像素值足不安全的,很难抵御朋文攻击。因此为了增强加密算法的安全性,增加扩散函数。
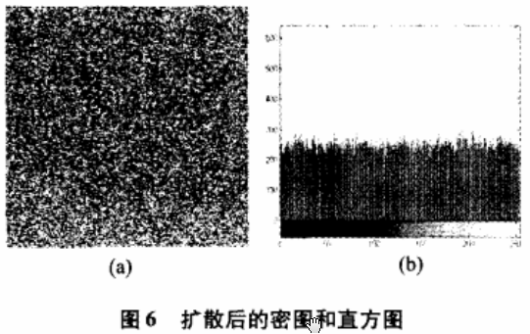
见式(10)。将置乱图像进行一次异或变换(扩散算法),可得到各灰度级下的像素点数趋于相同,这样更好的隐藏了图像的信息,从而可以抵御明文攻击。加密后,密图和直方图分别如图6(a)、(b)所示。
四、与其他混沌加密技术的比较
和其他混沌映射比较具有:
①更大的密钥空间
如Baker map最大为2N-1(N为图像的宽),而本加密的密钥空间理论上只和密钥长度有关,只要计算速度允许,秘钥长度可随之增加。
②对密钥变化更敏感
本图像加密算法将密钥设计为整个图像拉伸、折叠的数目,因此只要秘钥稍有变化,密图就会截然不同。但其他二维混沌映射基本都将图像分块的数目设计为密钥,拉伸、折叠操作都是对部分图像进行的。因此,用相似的密钥可以解密密图,降低了加密安全性。
③加密算法更加简单、清晰,易于实现
如Baker map的一般形式下的算法具有非常复杂的形式。而本加密算法非常简单,易于实现。
④加密速度快,能够实现实时加密
在一台Pentium M l.3Gffz的笔记本电脑上仿真表明,未优化的二维可逆映射的VC程序,运行速度约为3Mbpso能满足实时加密需要。
小知识之二维
在一个平面上的内容就是二维。 二维即左右、上下两个方向,不存在前后。在一张纸上的内容就可以看做成是二维。 即只有面积,没有立体。二维是平面技术的一种,例如普通的平面动漫,称之为二维动漫、简称二维。(富有立体感的是三维)。另外,脑海里的想象也可看做二维。











