由于时空混沌序列非常复杂,借助它来设计加密算法能有效提高其安全性。为此,我们设计了一款基于时空混沌的分组加密算法,该加密算法主要是通过迭代时空混沌模型来获取变换参数,然后利用这些参数来完成对分组的加密。算法以时空混沌模型内各点的初始状态作为密钥,这使得扩充密钥空间变得非常容易。
一、时空混沌模型
1、模型分析
在时空混沌模型中,内部各点在下一时刻的状态不仅与该点当前的状态有关,还与它在模型中的位置有关。耦合映象格子模型(CML: coupled map lattices)是时空混沌中的一种典型模型,其数值实验的效率非常高。本文选用耦合映象格子模型中的最近耦合形式作为产生伪随机序列的混沌映射,其数学表达式如下:
![]()
其中,Xn(i)为格子i在时刻n的状态变量,n为离散时间坐标,i为离散空间坐标,i=1,2,…,L,L为格子个数);ε∈(0,1)为耦合强度,f为局部函数,边界条件为Xn(L+i)=xn(i)。
CML模型具有如下特点:
1)模型是一个多维的混沌系统,格子之间相互耦合,整个系统产生的混沌序列比单个映射产生的序列更复杂。
2)耦合系数s,局部映射中的参数以及各格子的初始状态都可用作产生伪随机序列的密钥。适当调整格子个数可获取足够大的密钥空间。
3)模型中存在多个在空间和时间上的自由度,只有当所有格子的输出同时退化为周期序列时,整个模型才会退化为周期序列,退化后的序列周期会更大,可减弱计算机有限精度的影响。
模型的上述特点为设计加密算法奠定了很好的基础。
2、参数的选择
CML模型具有冻结化随机、缺陷混沌扩散和完全发展的混沌等多个状态。从设计密码系统的角度出发,应让模型处于完全发展的混沌状态。最近耦合CML模型的Lyapunov指数谱为:
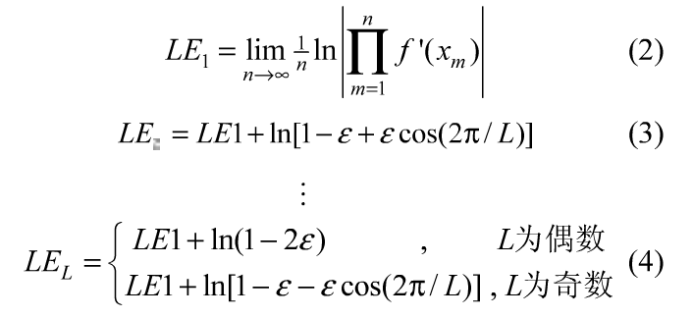
最大Lyapunov指数(LEi)对系统的混沌特性有至关重要的影响。LEi越大,系统的混沌特性越好。由式(2)知,模型的LEi与局部函数厂的LEi相同,只要f为混沌映射,则整个模型也就是混沌的。本文选用Logistic映射作为局部函数,即f(x)=μx(1-x),x∈(0,1),并设置u=4。另外,LE2大于0可以避免格子之间出现同步,且LE2越大模型就越快处于完全发展的混沌状态。从式(3)知,LE2随s的增大ε而减小,因此s应取小值。同时,考虑到格子间应保留一定的耦合强度,本文设置ε为0.08。根据Logistic映射的最大Lyapunov指数值和s为0.08,可得:
![]()
由式(5)知无论三的取什么值,LE2均大于0,即CML模型处于完全混沌的状态。
二、加密算法设计与仿真实验
1、加密算法
整个加密算法如图1所示。具体步骤如下:
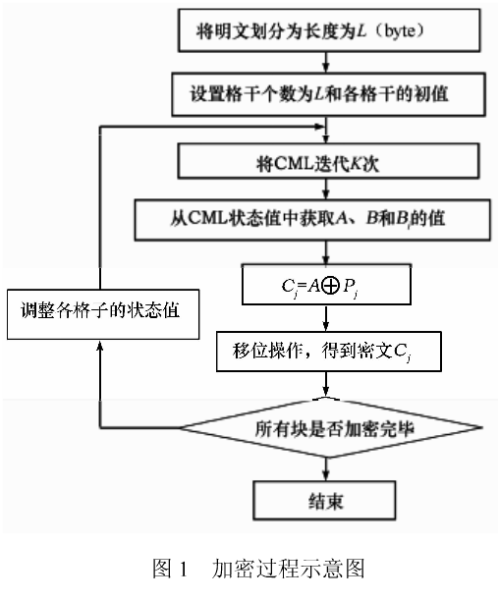
步骤1 将明文m划分成一系列长度为L(L≥8)字节的块Pj (j=1,2,…),最后一块若长度不够则补零占位。
步骤2 设置CML中的格子个数为三,以各格子的初值作为密钥,对应的初值为xo(i)∈(0,1),i=1,2,…,L。
步骤3按照式(1)将CML模型迭代K次得 XK(i),其对应的二进制形式为:
xk(i)=o.b1ib2i…,bni...其中b为第bni个i的小数点后第n比特的值。
步骤4依次从每个格子值中抽出其小数点后1~8bit,组成长度为L字节的序列A,即A=b11b21…b81b12b22…b7LbL,再依次从每个格子值中抽出小数点后的9~11bit,得到L个范围在0~7之间的数Bi,i=1,2,…,L,即Bi=b9ib10ib11i。对所有Bi求和,设所得结果为B。
步骤5将序列4与明文块P进行异或操作,得Cj=A+Pj。
步骤6设Cj(i)为Cj(i)中第i个字节,对Cj(i)循环左移Bi位(i=1,2,…,L),然后再对得到的整个数据块循环左移B位,产生加密密文0。整个移位过程如图2所示。
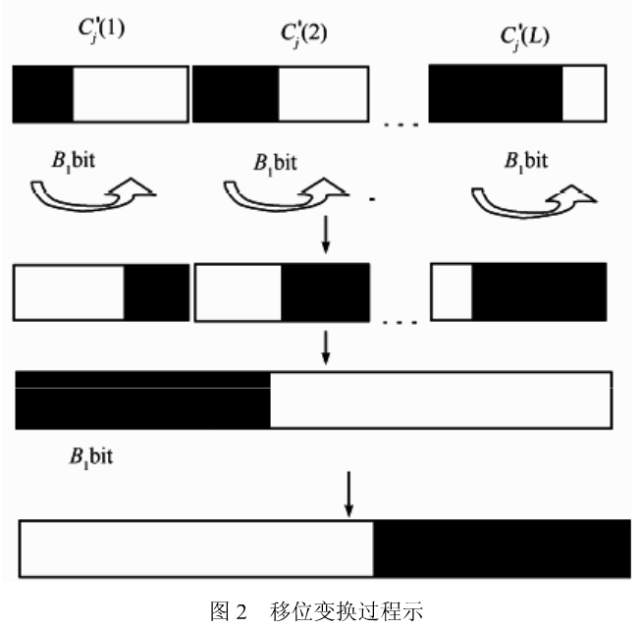
步骤7若明文块全部加密完毕,则结束;否则按照式(6)调节格子的状态值,然后转到步骤3。
![]()
其中,Pj(i)为明文块Pj(i)的第i个字节的数值。
及iam算法中的迭代次数K,利用卡方检测方式来确定,具体步骤如下:
1)将区间[0,1]划分为m个相等的子区间,表示为:
![]()
2)随机设置CML的初始状态,将其迭代K次,对应的状态变量表示为XK(i),i=1,2,…,L。然后,随机选择一个格子j,把微小变量△α加到xo(j)上,将CML再迭代K次,相应的状态变量表示为xk(i),i=1,2,…,L。重复上述过程,计算出S组xk(i)和xK(i)。
3)对CML中的每个格子建立一个m×n的频率表。表中单元格的值nef(e,f分别为表的行标和列标)为满足条件(e/m)<xk(i)<(e+1)/(m)和(f/m)<XK' (i)<(f+1)/(m)的数对xk(i)和xK(i)的个数。按照式(7)计算CML中每个格子的x2值。
4)取各格子中最大的x2值作为CML的X2值。
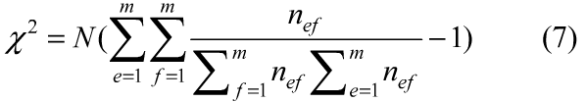
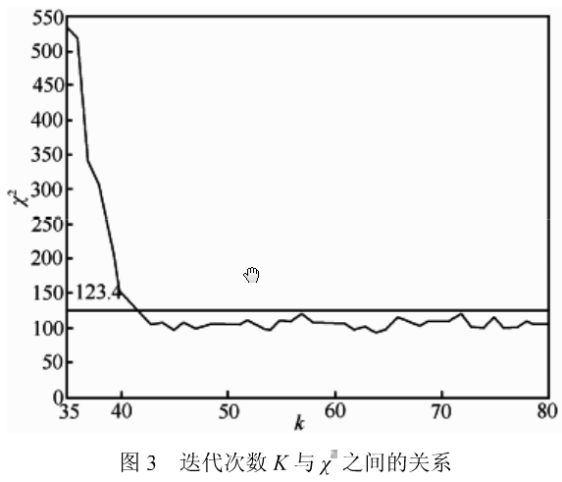
例如,设置格子个数L为1 6时,取m = 11,S=1000,△α= 0.000 1,得到CML的x2值与迭代次数K之斓的关系如图3所示。由于X2值小于5%对应的临界值时2个变量无关,在自由度为(m-1)(m-1)=100时,查x2表得临界值xk2为124.3。结合图3知,当K>42时,能保证2个迭代后的CML状态完全无关。考虑一定的富余,取K=45。
2、解密算法
解密过程与加密过程类似,首先按照相同方式获取A、B、Bi,然后,将密文进行循环右移变换,再进行异或运算产生明文。
3、仿真实验
加密算法具有较好的灵活性,通过调整时空混沌中格子的个数可调整加密分组的大小。此处设置格子个数为16,即加密分组大小为128bit。对图片Lena文件加密。原图像、加密图像及其直方图如图4所示。从中可以看出本算法有很好的混乱和扩散特性。

三、安全性分析
1、密钥空间分析
加密算法中的密钥为CML模型中格子的初始值。仅以计算机精度为10-4进行估算,各格子的取值范围为(0,0.9999],共有104个可取的值。在模型中格子个数不小于8的情况下,算法的密钥空间不小于1032>2100。实际上,目前计算机系统的计算精度远大于10-4,则相应的密钥空间会更大,拥有足够大的密钥空间,对于抵抗穷举攻击具有重要的意义。
2、信息熵分析
设信息为m,则其信息熵的计算式为:
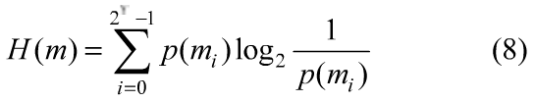
其中,p(mi)为信息值mi出现的概率。假设信息m共有28种状态值且出现的概率相同,则根据式(8)得H(m)=8,这表明信息是完全随机的。对信息文件加密后,总希望密文的信息熵尽可能的接近于理想值8,若信息熵小于8则表明从理论上看密文存在一定程度的信息泄漏。
加密后图片文件的信息熵值为7.998 9,接近于理想值8,说明加密过程中信息的泄漏非常小,加密算法是安全的。
3、混乱与扩散性能分析
混乱和扩散是加密过程中2个重要的步骤。加密算法在加密每个分组时使用的参数为A、B和Bi,它们均是通过抽取时空混沌模型内各点的状态值而得到。由于刻意避免了模型内各格子之间出现同步的可能,模型处于完全发展的混沌状态,因此能很好地保证A、B和Bi的伪随机性和对变换后明文的混乱性。
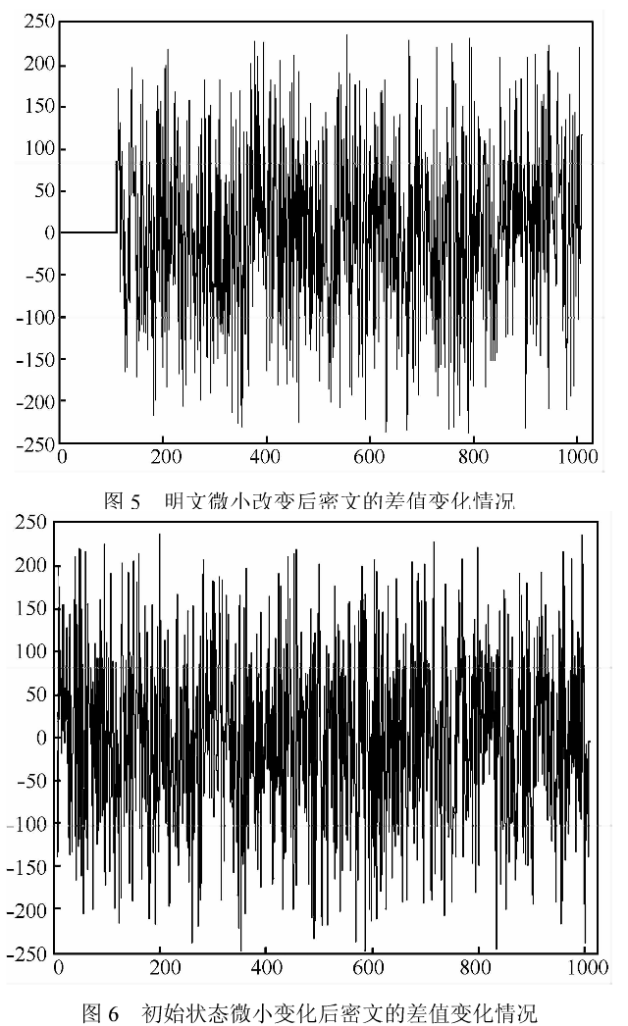
在加密新的明文分组之前,算法对模型中各格子的状态值进行了调整,并通过K次迭代来消除调整的直接影响。这不仅能保证每次加密时使用的A、B和Bi没有相关性,而且还使A,B和Bi与密钥相关的同时,与明文相关,进一步提高了算法的扩散性。为说明本文加密算法的混乱与扩散特性,以一个特殊的文本文件(由1 000个字符a构成)为例,分别对明文、时空混沌模型的状态初值进行微小的改变,具体如下:
1)将文件中第1 00个字符a更改为字符b;
2)将第一个格子的初始状态值由xo(1)=0.123 456改为0.123 457。
改变前后密文的差值如图5和图6所示。可以看出算法有很好的混乱和扩散性能。
小知识之Lyapunov
Lyapunov指数是衡量系统动力学特性的一个重要定量指标,它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率。对于系统是否存在动力学混沌, 可以从最大Lyapunov指数是否大于零非常直观的判断出来: 一个正的Lyapunov指数,意味着在系统相空间中,无论初始两条轨线的间距多么小,其差别都会随着时间的演化而成指数率的增加以致达到无法预测,这就是混沌现象。











