图像加密算法之多种混沌系统加密

随着计算机网络和信息技术的迅猛发展，多媒体通信逐渐成为人们彼此之间信息交流的重要手段。数字图像作为多媒体信息中最重要的1种信息表达形式，已经广泛应用于我们的生活之中。但是数字图像的传输存在着很多安全隐患，信息安全已成为日益严峻的现实问题。因此，研究图像加密具有重要的现实意义。

一、多种混沌系统图像加密算法原理

混沌现象是美国气象学家Lorenz 1963年在研究模拟天气预报时发现的。他把大气的动态方程简化成了三阶非线性方程（后来被称之为Lorenz方程），发现这个确定性方程的动力学演化具有类似随机的性质，发现了著名的Lorenz吸引子，因而推断出长期的天气预报是不可能的结论（即著名的“蝴蝶效应”）。混沌运动是自然界中客观存在的有界的、不规则的、复杂的运动形式，而且对初值的极端敏感依赖性。

1990年英国数学家Matthews最早将离散混沌动力系统应用于加密算法吲，混沌系统应用于图文件像加密，首先由Fridrich于1997年提出，使用二维的Baker映射和Cat映射进行了像素位置的变换．Chen和Mao在Fridrich的基础上，分别将二维Baker映射和二维Cat映射扩展到了三维，并分别利用三维映射提出了1种快速的图像文件加密方案。

1、Arnold映射

Arnold变换是俄国数学家Vladimir I．Arnold提出的，俗称描脸变换。猫映射的数学表达式为：

其中Xn+1，Yn+1，Xn，Y∈(o，1，2…．，N一1），a和b均为正整数。它实际上是一种像素点的位置变换，这种变换是一一对应的，并且可以进行迭代运算。

由于数字图像中像素值的个数有限，在进行有限的N次迭代变换后，图像会恹复到原始状态，即Arnold变换具有周期性，所以这种方法的加密对是不安全的，使用穷举法，从密文空间的任意一个状态开始进行迭代运算，都会在有限的运算次数内得到原始图像。

2、logistic映射和虫口模型

一维Logistic映射是一个简单的混沌映射，其数学表达公式为：

其中tk是状态，λ是参数，若选择参数无限制在[0，2]区间内，则上式将是从线段，I=[-1，1]到它本身的1个非线性映射，当逐渐增大时，迭代出现多次突变。当λ=λ∞=1.40115时，迅速达到周期N→∞；当λ>λ∞时，多次迭代结果看起来时分布在一定区间内的随机数，即进入了混沌状态。区间[丸，2]称为混沌区。

另1种Logistic映射‘别是生态学家May.R于1976年提出来的虫口模型，它是1个十分简单又具有重要意义的非线性迭代方程Logistic映射方程如下：

其中Xk∈(0，1)。μ为分支参数．当μ=3时，单线开始一分为二。在μ=1+√6处，开始出现了4周期。在此之后，大量的倍周期分支出现在越来越窄的μ间隔里，经过n次分支，周期长度为2n。这种周期倍化的过程是没有限制，但相应的μ有一个极限值：3.569 945 67...，当3.569 945 67<μ<4时便进入混沌区，这一过程具有很大的普遍性。

二、加密与解密方法

本图像加密算法采用Arnold变换结合logistic映射思路，实现改变图像像素的位置和图像像素素值，并增强图像加密的安全性Logistic系统对初始值的敏感性，把初始值作为密钥。破译者如果不知道确切的密钥，攻击密钥与真正的密钥有丝毫细微的差别，所产生的密钥序列都会有很大的不同，给破译增加了极大的难度。

1、图像文件加密过程

（1）读入一幅256*256的RGB模式彩色图片，RGB模式彩色图片共有3个通道，每个通道都有8位深度，即RGB模型为图像中每一个像素的RGB分量分配一个0-255范围内的强度值。将图
片分解成RGB二维图片并将三幅图转换成二维厌度序列M1，M2，M3。

（2）红色通道M1加密

Step1：将M1转换成一个长度为256*256的一维序列AA的像素点坐标用二维矩阵x1表示，利用Arnold变换处理后生成二维矩阵X2，其中Arnold矩阵参数为A=[1 112]，这样使一维序列
乱序后生成图片A1，二维矩阵X2也是以后要用到的解密矩阵。

Step2：选取初值xo=0.400 001，生成一个logistic序列L1，L1也是一个长度为256*256的一维序列，把Al序列与LJ序列中的各个元素一一对应，构造一个二维矩阵P，行的长度是4，列长度是256*256，我们把L1的元素放在矩阵P的第一行，A1的元素放在第二行，A1元素的行标放在第三行，列标放在第四行，这个二维矩阵也是我们以后要用到的解密矩阵。然后将L1中的元素进行排序，即对P矩阵的第一行进行排序，取出排序后的P1矩阵的第二行，得到一位序列A3，这样，A1序列中的元素也跟随混沌序列L1中的元素发生位置变换，生成密文序列A3。解密的方法也很简单，只需要分别对密文矩阵P1的第三行和第四行进行排序，那么得到的矩阵P2的第一行就是解密的结果。

Step3：选取参数μ=3.800 001，初值xo=0.600001，利用虫口模型生成一个长度为256*256的一维序列L3，为了增加密文的破解难度，将L3序列小数点后1、6、8位取出组成一个3位数，并对256求余，得到序列L5。

Step4：将A3与L5进行异或运算，生成A4，这就是最后经仄度加密后的红色通道密文。

（3）绿色通道M2加密

选取参数μ=3.900 002，初值xo=0.800 05，利用虫口模型生成一个长度为256*256的一维序列L31，因为混沌序列对初值非常敏感，L31序列与前面的L3序列有非常大的差异，这也有利于增加密文的破解难度，然后采用step2的方法，对绿色通道M2进行位置变换，M2经logistic的虫口模型乱序后生成一维序列A5。

（4）蓝色通道M3加密

采用step1的方法，对蓝色通道M3进行位置变换，M3经猫映射乱序后生成A6，我们可以把蓝色通道M3进行多次猫映射位置变换，这样增加了M3的破解难度。

（5）A4，A5，A6分别代表红绿蓝三色通道的密文，将这3个一维序列分别转换成256*256的二维序列，然后将它们分别映射成红绿蓝三色的分量，把它们组合后就是RGB模式的密文。

2、解密过程

（1）先对蓝色通道的密文进行解密A6经猫映射逆运算生成N1，其中变换矩阵A的逆阵为A-1=[1-1-12] ，如果蓝色通道M3经过多次猫映射乱序加密，那么解密也需要经过相同次数的逆
映射解密。

（2）在对绿色通道的密文进行解密采用Step2的解密方法，A5经logistic重新排序后生成N2。

（3）对红色通道的密文解密需要先把A4与L5再次异或生成N3，这是对厌度值的解密过程。

（4）采用Step2的解密方法，N3经logistic重新排序生成N4。

（5）N4经猫映射逆运算处理生成N5。

（6）N1，N2，N5组合后是解密后的彩色图片。

三、仿真实验效果

将原始图片转成RGB三色通道，见图1。

将三色通道图片转换成厌度图片，然后分别加密，得到以下3个密文图片，如图2所示。

将3个密文图片后合成彩色RGB模式的密文图片，见图3。

四、图像加密算法分析

1、直方图分析

直方图(Histogram)又称柱状图、质量分布图，是一种统计报告图，由一系列高度不等的纵向条纹或线段表示数据分布的情况。一般用横轴表示数据类型，纵轴表示分布情况。对图像文件加密的攻击方法很多，其中一种就是对图像进行直方图分析，由于G通道和B通道采用的是像素点位置变换的加密方法，这种方法不改变图像的直方图，而R通道的加密方式是先改变像素位置，再改变像素的仄度值，因此叵方图也发生了变化，图4是尺通道的直方图变化图。

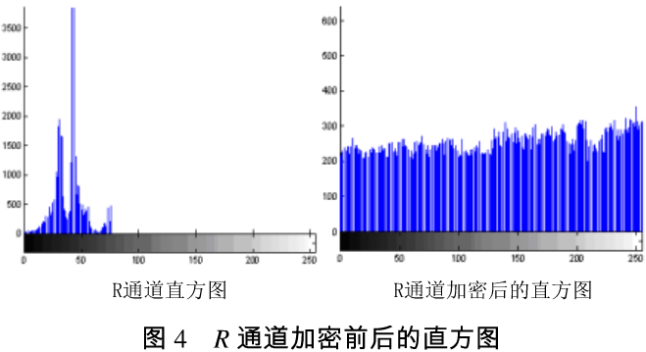
2、密钥敏感性分析

密钥的敏感性是指当初始密钥发生微小变化时，密文的变化程度，我们用混沌算法对矩阵变换的效果图来检测算法密钥的敏感性。

对logistic公式进行敏感性分析，我们分别采用不同的参数(在a=3.6的情况下，分别采用初始值xo=0.400 001和xo=0.400 002)来分析加密算法的敏感性。由图5可以看出，不同的x0和以值对像素点置换后的影响很大，当我们稍微变换x0和a的值时，就能得到很不一样的加密后的图片。不断变换x0值和a值，就有很多的变换，对图片文件进行加密后，攻击者想破解密文就有了很大难度。

3、相邻像素的相关性分析

图像相邻像素间的相关性，可以具体的反映出图像中像素点的置乱效果。由图6一图8可以看出，未加密前的图像，相邻的几个像素点的仄度是非常接近的，于是不管是水平、对角线还是
垂直相关度，它们的分布图都基本在y=x这一条直线上，而经过加密后的图像，由图的分散程度可以看出，各个像素点的临近的像素点都不再是以前的，而得到的相关性图越分散，说明图像被置乱程度越明显，加密的效果也就越显著。

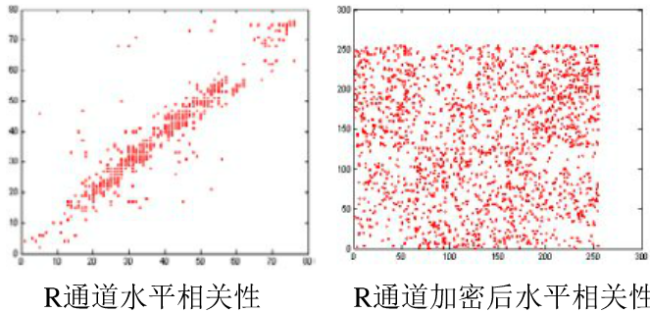
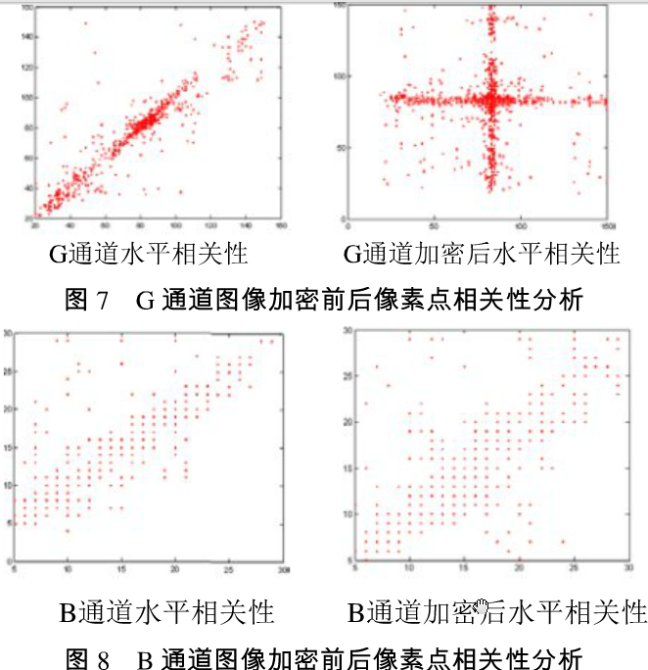
由图6一图8可以看出，R通道和G通道的图像被置乱程度非常显著，B通道的置乱程度很一般，这是因为B通道采用的Arnold映射只进行了1次迭代，如果进行多次迭代，加密的效果要好
得多。

admin普通用户

海报分享