光学加密系统之公匙密匙分配体制加密

针对光学变换加密系统的密匙安全管理和分发问题，提出了基于公匙密匙分配体制和光学变换的混合加密系统，首先利用光学加密系统对原始图像文件加密，然后对光学加密系统的工作密
匙进行压缩，最后利用公匙密匙分配体制对压缩后的密匙进行分配和管理。解密时，接收方不需要等待，就可以预先利用公匙密匙分配体制获得解密密匙。

一、基于光学变换的双相位序列加密系统

在现有的光学加密系统中，大部分是基于某种光学变换而实现的，具体系统模型如图1。

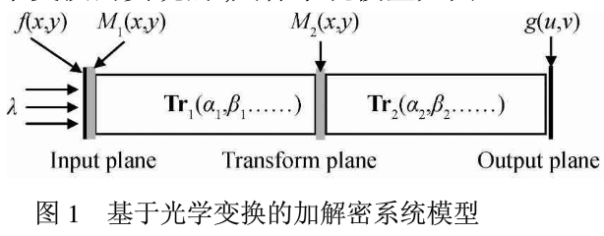
其中λ为照射光波长，αi，βi…为光学变换系统参量，( x，y)，(x',y')和(u,v)分别为输入面、变换面和输出面的坐标，在加密阶段，待加密图像f(x，y),在输入面与相位掩模M1(x，y)相乘，然后通过光学变换Tr1，在变换域与相位掩模M2(x',y')相乘，再通过光学变换Tr2，最后在输出面得到加密图像g(u,v)，整个加密过程可用式(1)表示为：

从上述加密过程可以看出，波长λ、变换系统参量α1，β1……、α2，β2……以及M1_( x，y)和M2(x',y')一起为密匙设计提供了巨大的空间，解密时，缺少其中任何一个都不能恢复原图像，密匙空间非常大，系统安全性能非常高。因此，从安全角度来衡量，这样的加密系统是最优的，但是由于该系统在加密和解密时使用是相同的密匙，因此它仍然属于对称加密系统，系统的安全性能完全依赖于密匙的安全性，为了保证密匙的安全分配和管理必须采取其他办法，如果又采取对称加密技术对密匙进行加密传送，将会陷入无休止恶性循环，显然是不现实的，为了解决这个问题，一些学者提出一种基于公匙密码体制的光学混合加密技术，先利用传统的光学变换系统对原图像文件加密，然后利用公匙密码体制对系统密匙（工作密匙）进行加密，从而实现系统密匙的安全分发，虽然公匙密匙加密系统对于安全通信似乎是理想的，但是它的最大缺点就是加密和解密速度远不如对称密匙加密系统，因此采用公匙密码体制对长度比较大的工作密匙（如相位掩模）进行加密解密速度非常慢，而且解密方要等到接收到加密的工作密匙后，才能对它进行解密获得工作密匙，从而造成整个混合加密系统的加密效率非常低，因此，该技术虽然解决了密匙分配和管理问题，但是并没有显示出速度的优势。

二、基于公匙密匙分配体制和光学变换的混合加密系统

针对加密技术的缺陷，在综合考虑系统安全和速度的基础上，提出一种基于公匙密匙分配体制和光学变换的混合加密系统。与基于公匙密码体制的光学混合加密系统不同的是，不是直接利用公匙密码体制对光学系统的工作密匙逐个进行加密，而是先对光学系统的工作密匙进行压缩，然后利用公匙密匙分配体制对压缩后的工作密匙进行分配和管理，这样将大大增强系统的效率。

在光学加密系统的工作密匙中，相位掩模的长度是最长的，为了节省时间，在利用公匙密匙分配体制对它进行分配之前，必须对它进行压缩处理，在常用的相位掩模中，虽然随机相位序列具有极高的安全性能，但是由于序列中的元素具有完全随机性的特点，因此不能用一个确定的数学方程或公式进行重构，而混沌序列的类随机性和确定性特点，既保证了极高的安全性能又能利用非线性叠代方程进行重构，对于特定的非线性叠代方程，只要控制初始值，便可控制整个序列，因此用混沌序列来构造相位掩摸便于重构和压缩，另外，系统的其他工作密匙α1，β1……、α2，β2……，也可以令它们为混沌序列某一位置的元素，对于那些系统工作密匙中还包括波长和焦距的变换系统，如广义分数傅里叶变换系统，由于波长和焦距的具体大小不能为任意值，供它选择的数值范围有限，因此把它们作为公共参量，对系统安全影响不大。这样，光学加密系统中的所有的工作密匙，除了波长和焦距以外，均可由一混沌序列来确定。解密时仅用相应的初始条侏从确定性系统获得浑沌序列重构相位阵列和其他系统参量即可获得工作密匙，对于上述系统，由于原来的工作密匙已被压缩到只有一个，即混沌序列的初始值，因此这个初始值对系统的安全显的至关重要，为了保证对它进行安全分发和管理，我们利用公匙密匙分配体制对它进行分配，本文所采用公匙密匙分配体制是由美国学者Diffie- hellman提出的，它的理论基础是有限域上指数函数的单调性，即计算有限域上的指数很容易，但是计算有限域上对数的整数解很困难，具体分析如下：设q为素数，则在具有q个元素的有限域上的指数可以表示为：

式中g为有限域上的原根，且1<g<q，x分布在有限域上的所有非零整数元素集上，当日为素数时，y也是分布在有限域上的所有非零整数元素集上，从式（2）不难推知，x可以表示为在有限域上以g为底y的对数，即：

根据式（2），已知x计算y十分容易，但是已知y利用式(3)计算x却极其困难。Diffie-hellman密匙分配体正是利用这种单向性构成的，在具体用它进行密匙分配时，其协议如下：

系统中的每一个用户都从整数集{1，2，3，q-1}，上随机选择一个数作为自己的私密密匙，例如用户A和B选择的私密密匙分别记为xa和xb。然后根据式(2)计算出ya和yb为：

式中q、g均为Diffie-hellman体制已知的公共参量，用户A和B分别将ya和yb作为自己的公开密匙，连同自己的姓名、地址一起放到系统的用户公开密匙簿中，当双方需要通信时，通过式（6）：

即可获得工作密匙，计算速度非常快，易于实现，但是在不知私匙的情况下，却十分困难。

根据上述公匙密匙分配体制，在加密前，通信双方根据式（6）获得混沌序列的初始值，考虑到式（6）中的kab是一个在1到q-1范围内的整数，而混沌序列均为0到1范围内的小数，因此令混沌序列的初始值为：

然后利用式(8)所表示的非线性叠代方程获得混沌序列{Xk,k=0，1，2，3…n}。

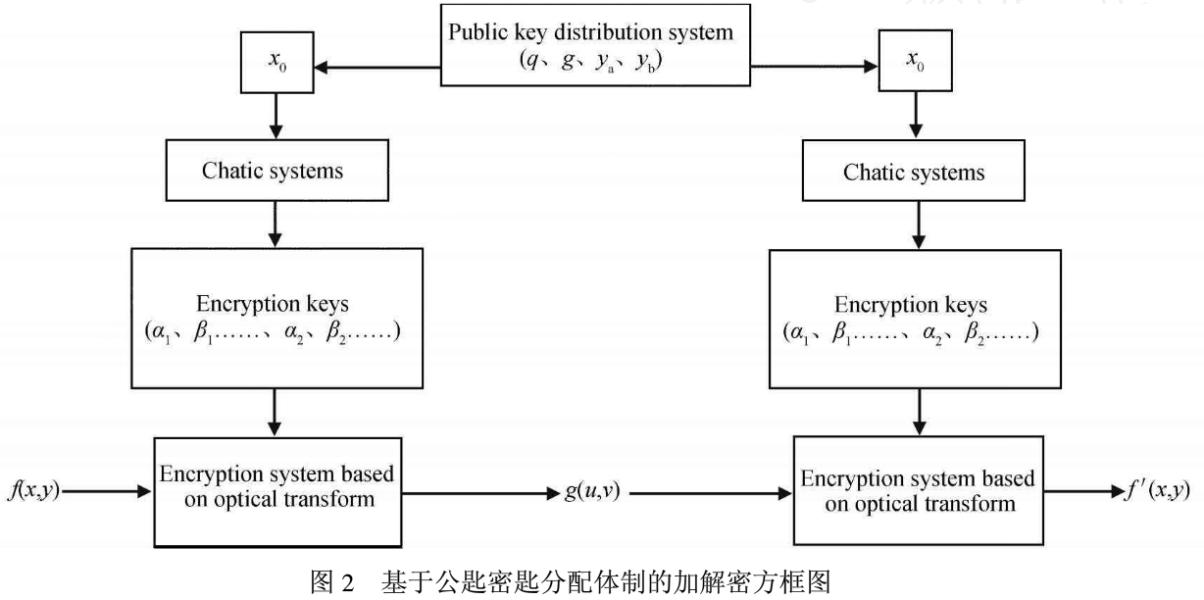
式中γ为控制参量，对于上述叠代方程，当控制参量取值在3. 569<γ<4.000范围内时，迭代结果出现了混沌现象，且Xk为0到1范围内混沌序列，如果原始图像大小为M×N，则在混沌序列Xk中选取2M ×2N+n（n为系统参量的总个数）个元素构成光系统的加密密匙对原始图像文件加密，接收方按照同样的方法获得解密匙对加密图像文件进行解密，具体加解密方框图如图2。

三、实验仿真

为了验证方法的可行性，以广义分数傅里叶变换系统作为加密系统为例，利用Matlab进行了仿真实验。实验时，公匙密匙分配体制中的公共参量g为3，g为524 287(越大保密强度越高，由于普通电脑的运算准确度只有15位，所以取的比较小），私密密匙xa为29，xb为33，然后根据式(4)和(5)得到公开密匙），ya=59 601，yb=65 358，并把它们和公共参量、姓名、地址一起放到系统的用户公开密匙本中，加密方利用自己的私密密匙xa和系统参量以及公开密匙yb根据式(6J得到Kab=387 606，然后利用式(7)获得混沌序列的初始值x0=387 06/524 286并生成混沌序列，其中γ取3. 68。为了确保越过瞬态过程，在记录序列之前先摔掉前400位，同时考虑到此时的系统参量α1、β1、α2、β2 （分别为输入和输出面离透镜的距离且以米为单位）和相位掩模实际制造的精确度，利用四舍五入只取到小数点后两位，图3(a)是以xo=387 606/524 287作为初始值生成的混沌序列A；图3(b)是以xo=387 605/ 524 286作为初始值生成的混沌序列B；图3(c)是它们的差值A-B。

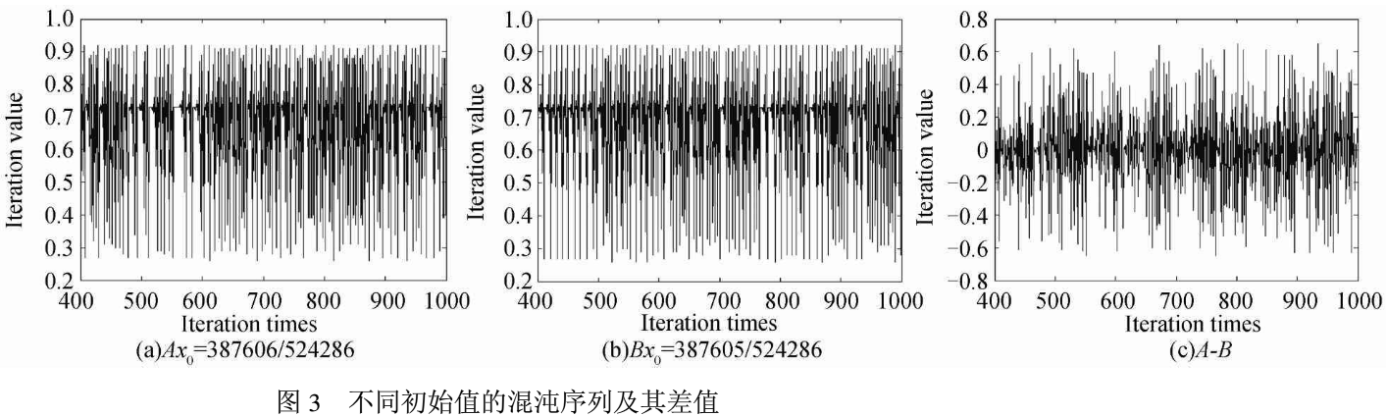
从上图可以看出，虽然我们只取到小数点后两位，但是两者差别非常很大，因此抗攻击能力非常强。选取混沌序列的第忌到k+3位元素0.77 0.640. 83 0.51分别为α1、β1、α2、β2，第k+4到k+3+M*N位元素生成相位掩模Mi，第k+4+M *N到k+3+2M *N位元素生成相位掩模M2(在这里k取401，M和N均取128)。图4(b)和4(c)分别是M1和M2的实部分布，图4(d)是最后的加密图像，其中照射光波长为632.8 nm，透镜焦距分别为30 cm和40 cm.接收方接收到加密图像后，利用自己的私密密匙xa和系统参量以及公开密匙ya根据式(6)得到Kab=387 606，然后按照同样的方法获得解密密匙，图4(e)是利用正确密匙的解密图像，图4(f)是错误密匙的解密图像r Kab =387 605)。

四、系统效率和安全性能分析

从加密解密原理和仿真过程来看，利用公匙密匙分配体制对光学系统工作密匙进行分发，加密方先利用公匙密码体制对光学系统工作密匙特别是相位掩模中的元素逐个进行加密，并通过特定的通道进行传送，然后接收方接收到加密工作密匙并利用公匙密码体制解密光学系统的工作密匙。公匙密匙分配体制是把光学系统中所有工作密匙作为一个整体进行分发，只要通信双
方按照事先约定好的公共参量，不需要通过任何通道进行传送，便可获得光学加密系统的密匙，即接收方不需要等待，就可以预先获得光学系统的解密密匙，克服了公匙密码体制速度慢过程复杂的缺点，大大增强了混合加密系统的效率。

对于系统的安全性能，首先，根据Diffie-hellman体制的原理，其保密性强烈地依赖于模数q的大小，为了提高保密强度，可以选择足够大的模数，如100位，如果破解一次所需要的时间为1 min，可以粗略估计出采用穷举法破解的整个时间大约为94年，况且破解一次的时间再加上利用光学方法进行验证的时间大大超过1 min，因此就Diffie-hellman体制的设计原理来话，系统是足够安全的，另外，在选取混沌序列作为工作密匙时，虽然进行了四舍五入，只取到小数点后两位，但是由于混沌序列对初始值高度依赖性，保证了所选取的密匙因初始值的细微差别而截然不同，这样并不会降低穷举法攻击的难度。

admin普通用户

海报分享