二值图像加密之Arnold变换加密
在数字水印方案中,单纯地用各种信息隐藏加密算法对秘密信息进行加密是不安全的,因为攻击者只要破解了加密算法,就可能直接提取出秘密信息。针对这一点,我们提出在秘密信息隐藏之前,先对其进行置乱处理,使其失去本身原有的面目,再隐藏到载体中,以确保信息的安全性。以Fibonacci变换和Arnold变换的实验结果阐述了数字图像置乱方法在数字水印中的作用,并提了出一种利用Arnold反变换恢复图像的方法。
一、数字图像置乱的目的
到目前为止,比较成熟的信息隐藏算法基本上都是以图像作为载体的。图像置乱,顾名思义,就是把图像打乱,隐藏原始图像的真实内容。数字图像置乱和信息文件加密思想类似,它主要是通过对数字图像的像素位置做变换来“扰乱”图像,使其变得面目全非、杂乱无章,从而隐藏图像所要表达的真实信息。图像置乱可以达到两个目的:
1、加密处理
图像置乱变换是一种基于内容的图像加密方法,与不知道密钥对已加密信息进行解密一样,倘若不知道图像置乱所采用的算法,同样难以恢复原始图像的信息。
2、增强图像伪装的鲁棒性
置乱技术作为信息隐藏的预处理手段,可以大大增强图像信息伪装的鲁棒性。主要体现在3个方面:
①图像置乱以后,将得到一幅杂乱无序的图像,没有内容,没有纹理,也没有形状,从中无法读取出有意义的信息。
我们将这样一幅“三无”图像嵌入到另一幅普通图像里时就不易引起这幅图像在内容、纹理、形状上的太大改变,甚至觉察不出发生了改变,这样人眼就不易识别,从而逃出了第三方的视线,可以更好地保证水印信息的隐蔽性。
②由于秘密图像是置乱以后的图像,第三方难以对它的内容、纹理、形状等进行统计分析,这样即便他们截获到了秘密图像,也对此无能为力。如果第三方企图对秘密图像进行反置乱运算,这也是非常困难的,因为图像置乱的方法很多,每种方法又可以使用不同的置乱算法,设置不同的参数,加密方可以根据自己的想法得到很多不同的结果,这给企图进行反置乱的第三方带来了很大的困难,需要耗费巨大的计算量来穷举测试各种可能性。
③如果第三方进行反置乱运算不成,也可能会在隐蔽的载体上进行恶意修改,用置乱的方法也可以达到抵抗这些攻击的目的。因为合法接收者对秘密图像进行反置乱的时候,会使第三方在图像上所涂画的信息分散到画面的各个位置,形成点状的随机噪声,对视觉影响的程度不是很大。

图1是在置乱图像上进行涂改和剪裁两种恶意修改以后,恢复出的秘密图像。可以看到,秘密图像的内容依然可见。为了使提取的图像信息更为清晰,还可以对破坏严重的图像进行中值滤波等方面的处理,以去除随机噪声。
当然,不应该忽视的是图像置乱在一定程度上增加了加密计算的复杂度和计算量,但是与非法攻击者可能花费的更大的计算量相比,图像置乱仍是一种值得付出代价的、相对安全的手段。正是因为如此,图像置乱技术在数字水印技术中具有非常重要的作用和意义。
二、数字图像置乱的方法
数字图像的置乱可以在位置空间、色彩空间、频率空间上进行。随着计算机技术和数字图像处理技术的发展,很多文献对图像置乱提出了不同的置乱算法,大体上可以分为线性变换、几何变换和仿射变换。目前研究较多的置乱技术包括Fibonacci变换、Arnold变换、Hilbert曲线变换、E-曲线变换、Gray变换、仿射变换、幻方、正交拉丁方变换等方法。无论哪一种置乱技术都是可逆的,或者是具有周期性的,即多次迭代或者做反变换均能恢复原图像。
下面仅以Fibonacci变换和Arnold变换为例讨论数字图像置乱。
1、Fibonacci变换
1200年意大利数学家Leonardo Fibonacci提出了著名的Fibonacci数列,将Fibonacci数列应用于数字图像变换,可以得到Fibonacci变换。Fibonacci变换的原理是先作x轴方向的错切变换,再作相对于x轴的对称变换,然后作y轴方向的错切变换,最后的模运算相当于切割回填操作,其变换如图2所示。
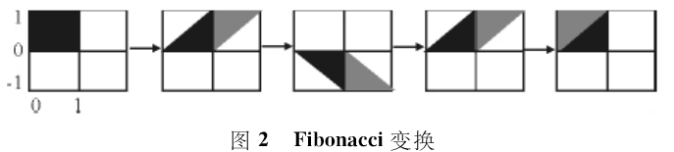
利用Fibonacci变换置乱效果图如图3所示。

Fibonacci变换是具有周期性的。对图像反复进行Fibonacci变换,当迭代到一定的步数时,就可以重新恢复到原始图像,Fibonacci变换的周期如表1所示。

2、Arnold变换
Arnold变换是V.J.Arnold在遍历理论的研究中提出的一种变换,原意为catmapping,俗称猫脸变换。Arnold变换直观、简单、具有周期性,使用非常方便。Arnold变换的原理是先作x轴方向的错切变换,再作y轴方向的错切变换,最后的模运算相当于切割回填操作,其变换示意图如图4所示。
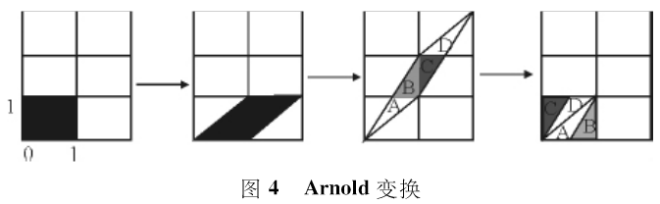
Arnold变换的置乱效果图如图5所示。

当对图像进行Arnold变换时,就是把图像的各个像素点位置按照下列公式进行移动,
![]()
从而得到一个相对原图像比较混乱的图像。对图像每进行一次Arnold变换,就相当于对该图像进行了一次置乱,一般来说这一过程需要反复进行多次才能达到令人满意的效果。利用Arnold变换对图像进行置乱后,使原本有意义的图像变成了像白噪声一样无意义的图像,从而实现了信息的初步隐藏。同时置乱次数可以作为水印系统的密钥,从而进一步增强系统的安全性和保密性。
Arnold变换也是具有周期性的。F.J.Dyson和H.Falk在分析离散Arnold变换的周期性时,给出了这样的结论:对于任意的N>2,Arnold变换的周期L≤N2/2。这是迄今为止最好的结果。计算Arnold周期的方法,对于给定的自然数N>2,下式的Arnold变换周期M是使得它成立的最小自然数n。
![]()
例如,尺寸为32×32的二值水印图像,根据文相关结论,大小为32×32的二值图像置乱迭代6次置乱度最大。所以N=32,对水印置乱的次数k=6(k可作为密钥),可以算出N=32时,周期M=24。因此,如果开始对水印置乱了6次,那么在提取水印后还要再对水印置乱24 -6—18次才能得到原来的水印图像,如图6所示。

图像的大小与Arnold变换的周期的关系,如表1所示。

3、Arnold反变换
如前所述,Arnold变换是具有周期性的,反复使用Arnold变换,可以在某一时刻恢复原始图像。但是Arnold变换的周期性与图像的大小有关,如果我们利用它的周期性来达到恢复原图的目的,势必要花费很长时间。然而在实际应用中,应该尽可能地减少计算时间和计算量,我们希望Arnold变换的周期越短越好,所以在设计数字水印图像的大小时,我们往往会选择Arnold变换周期比较小的图像,而这也在一定程度上限制了图像的选择,而且选择图像前需要事先计算出它的周期,从而增加了工作量。这个问题可以通过Arnold反变换的方法解决。
Arnofd变换式为:
![]()
假设:
![]()
其中,t1,t2为整数,则:
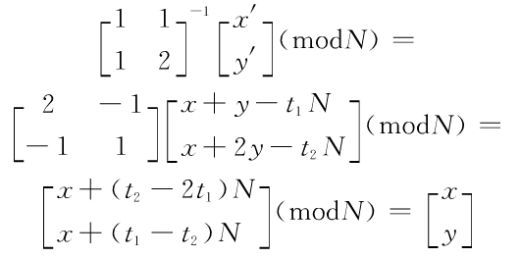
则Arnold反变换为:
![]()
用数学归纳法可以证明,当作n次变换时,即:
![]()
时,Arnold反变换为:
![]()
其中,(x,y)是原图像的像素点,(x',y')是变换后图像的像素点。利用Arnold反变换式可以将水印图像进行恢复。
由以上可以得出,对一幅置乱m次的图像进行恢复时,只要恢复后的图像的置乱次数k满足0≤k≤m,图像的恢复都可以通过对置乱图像作m-k次Arnold反变换得到,显然当k=0时,反变换后的图像就是原图像。
Arnold反变换的方法使Arnold变换置乱图像的恢复不再需要计算出图像变换的周期,并且可以恢复到图像的任意次置乱效果,恢复的效率大大提高了。
三、图像置乱效果的评定
通常,图像置乱度的评定应该主要考虑以下几个方面:①像素移动的距离;②像素分散的均匀度;③相对于原始图像差别;④图像视觉感知效果。
一般来说,置乱后的秘密图像越“乱”,它的隐蔽性越好,安全性也越高。从置乱变换的概念可以看出,位置空间置乱的实质就是将原始图像各个像素的位置进行了移动,从直观上来看,像素移动的距离越大,其置乱程度也就越大。另一方面,像素位置发生移动以后,像素分散的均匀程度也是要考虑的一个问题。如果图像的局部像素都向同一个方向平行移动的话,那么即使平移的距离很大,它置乱效果也是不理想的。
一般说来,原来集中在一起的像素,置乱以后分散得越均匀,图像的置乱效果越好。再者,置乱变换的目的就是最太限度地隐蔽原始图像的信息,因此,置乱图像相对于原始图像的差别越大,其置乱效果越好,因为置乱变换虽然不改变原始图像像素的灰度值,但是它会改变像素点邻域的灰度值分布,所以置乱图像相对于原始图像越“乱”,表明该置乱算法越有效。
小知识之二值图像
二值图像 binary image是指每个像素不是黑就是白,其灰度值没有中间过渡的图像。二值图像一般用来描述文字或者图形,其优点是占用空间少,缺点是,当表示人物,风景的图像时,二值图像只能描述其轮廓,不能描述细节。这时候要用更高的灰度级。











