基于双混沌和延迟Fibonacci数列的手机加密算法以一维Logistic映射作为混沌模型,采用双混沌系统增加控制参数,使混沌行为更加复杂;利用延迟Fibonacci数列对混沌进行扰动处理,使融合后的序列更具有随机的特征;将明文参与到加密算法中,给密文生成带来不确定性,使局部攻击更加困难,在密码不变的场合更能发挥保护作用。
一、混沌模型设计
混沌是指确定性系统中出现的类似随机的过程,它不同于一般的随机性,而是非线性系统在没有外界随机因素影响的情况下,因系统状态对初值的敏感性而产生的一种内在的随机性。混沌现象是非线性动力学系统中出现的确定性的伪随机过程,这种过程是非周期的,整体上稳定而在局部上具有扩张性。
Logistic映射是一类被广泛研究的动力系统,具备混沌运动的所有基本性质。定义如下:
![]()
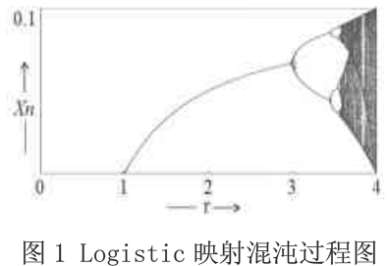
(1)式中γ称为分支参数。当3.56<γ≤4时,Logistic映射工作于混沌状态,产生的序列{Xn}呈现出随机性、确定性和遍历性等特征。
在不同初值下,对Logistic映射进行迭代,结果见表1。由表可见,当初始值X0相差仅0.001时,通过多次迭代后(50次、100次),序列的差别却越来越大,呈现出初值敏感性特征。
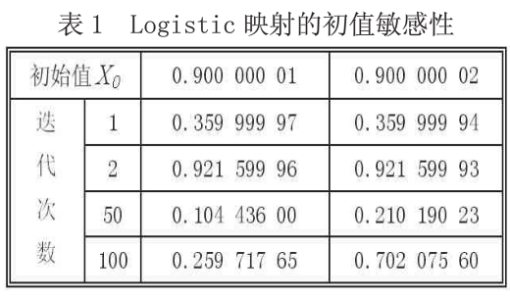
在Visual Basic 6.0环境下对Logistic迭代过程进行全程跟踪测试,当初始条件进行微小的改变时,生成的混沌序列呈现明显的分叉现象,如图1所示。
二、混沌扰动处理
Fibonacci数列产生的随机数具有明显的相关性,对经典的Fibonacci数列改进得到延迟的Fibonacci数列,利用得到的数列对混沌进行扰动处理。延迟Fibonacci数列如下:
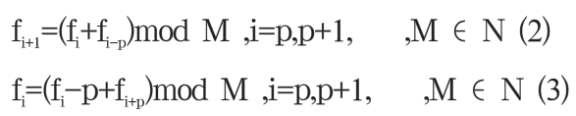
延迟Fibonacci数列中的任一项由它的前一项或前几项产生,这样可以使产生的序列克服不居中的缺点,改进后的Fibonacc1数列和原来的数列一样,具有产生随机数速度快、算法简单、容易实现等优点。
混沌映射产生的随机数列在理论上是无周期的,由于受计算机处理浮点数的精度的限制,往往得不到需要的数列,产生的延迟Fibonacci数列和其他方法产生的数列一样也存在着一定的缺陷,同样存在着明显的序列相关性。因此,利用一种发生器产生随机数列的方法总是不能克服自身的缺陷,可以利用不同发生器的良好特性组合使用它们,往往会得到良好的效果,所以组合使用随机数发生器,对它们实行融合,不仅可以克服自身的缺点,也可以改进数列的性能,也能满足实际应用的要求。
三、基于双混沌和延迟Fibonacci数列的手机加密算法设计
系统的初始状态由用户输入来确定,基于双混沌和延迟Fibonacci数列的手机加密算法结构框图如图2所示。
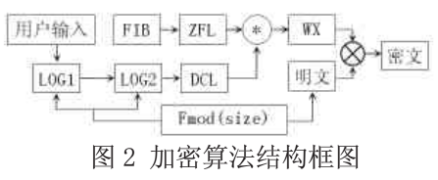
1、基于双混沌和延迟Fibonacci数列的手机加密算法描述
步骤1:设计使用2次映射Logistic过程实现混沌的置乱,密钥流经过LOG1混沌一次后输出,由LOG2进行再混沌,LOGI与LOG2复合产生双重的混沌轨道,使混沌行为更加复杂,难以分析和预测,抵御重构攻击。
步骤2:选取(3)式作为扰动序列FIB,控制参数为fo,M,P。初始循环一定次数后输出整数扰动序列ZFL。
步骤3:将双重混沌序列映射到整数空间ZM上,这是一个一一映射,即与ZFL做乘运算得到伪随机数列WX。
步骤4:用所得伪随机序列WX与待加密数据文件(明文)进行异或运算得到加密的数据文件(密文)。基于双混沌和延迟Fibonacci数列的手机加密算法是一种序列密码加密算法,加密端加密明文信息,然后将密文发往解密端,解密端收到密文后,在相同的初始条件下进行混沌重现,解密出明文。加密端和解密端是两个完全相同且彼此独立的混沌系统,两系统间不存在耦合关系。同时,基于双混沌和延迟Fibonacci数列的手机加密算法为对称加密算法,解密过程与加密过程同理。
2、系统初始状态敏感性测试
取x0=0.2,μ=3.92,λ=3.64, 迭代50次,其行为如图3(a)、(b)虚线所示。

步骤1:取x0=0.20001,μ=3.92,λ=3.64,迭代50次时其行为如图3(a)实线所示。从对比结果可以看出,初始输入值相差0.0001,经过DLOG系统的迭代演化,误差在迭代23次就开始被放大,即呈现出比较好的初值敏感性。
步骤2:取x0=0.3,μ=3.92,λ=3.64, 迭代50次时其行为如图3(b)实线所示。从对比结果可以看出,初始输入值相差0.1,经过DLOG系统的迭代演化,误差在开始间断就开始被放大,满足加密的需要。
四、试验测试与结果分析
应用算法针对CDMA寻址方式的连通用户设计了一个密码验证系统,分别实现对汉字和图片文件加密解密的仿真试验,结果证明该加密算法是一种有效的加密算法,进一步提高了抗破译性,可以有效地保护数据。
1、汉字加密
中国是世界上手机用户增长最快的国家,对手机中汉字的加密工作越来越重要。在Visual Basic6.0环境下,模拟手机用户进行了加密与解密测试。
步骤1:对汉字进行数据文件加密。在加密文本框中输入明文数据文件,输入密码(如“lv1234"),保存的文件名为aaa.txt;打开加密的文件aaa.txt可以看到,加密后的数据已经无法识别,如图4(b)所示。

步骤2:解密。打开加密文件,输入正确密码(如“lv1234”),解密后可以看到还原出来的数据和初始数据完全一致;输入密码(如“yan123’’),解密后的信息可以看出和原文差别极大,已经无法识别,如图4(c)所示。
2、图像文件加密
随着多媒体、通讯和网络技术的飞速发展,除文本外,图形、图像、声音等多媒体信息广泛应用于通讯领域,它以直观、形象、快速等特点得到了人们的共识,但一些重要的数据在传输过程中如果被他人截获是很危险的,因此在存储和传输多媒体信息时也必须进行加密处理,对图形和图像文件加密是对多媒体信息保护的一种很好的方法。
在Visual Basic 6.0环境下,采用设计的加密解密系统对各种格式的图像文件加密和解密测试,仿真实验结果如图5所示。

五、基于双混沌和延迟Fibonacci数列的手机加密算法的特点
(1)充分利用混沌对初值的敏感性,双重混沌增加了控制参数,使混沌行为更加复杂,难于重构。
(2)提供很大的密钥集,在不知道密钥的情况下,进行穷举破译困难。
(3)扰动的方法实现有限精度的混沌序列,使融合后的序列更具有随机的特征。
(4)明文长度参与到加密中,更给密文生成带来不确定性,使局部攻击十分困难,在密码不变的场合更能发挥保护作用。
(5)针对汉字存储特点采用双字节加密,增大密文可变空间,更进一步提高了数据的安全性。
如果将混沌技术应用在电信用户的密码认证上,使用混沌序列码对信息进行加密,可以其处于无序码的保护状态下,增强手机用户信息的抗破译能力,这将是电信系统信息安全技术一次新的突破。
小知识之Fibonacci数列
Fibonacci数列,又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、……在数学上,斐波纳契数列以如下被以递归的方法定义:F0=0,F1=1,Fn=F(n-1)+F(n-2)(n>=2,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1960年代起出版了《斐波纳契数列》季刊,专门刊载这方面的研究成果。











