基于混沌的图像文件加密方法在安全性、适应性上都具有优势,我们在对原有的混沌图像加密算法安全性分析的基础上,提出了一种基于Logistic和Chebyshev双混沌映射的数字灰度图像加密算法。
一、Logistic与Chebyshev混沌系统简介
Logistic映射是一个源于人口统计的离散时间动力学系统,其定义为:
![]()
式中:xn表示状态变量第几次迭代的值;u为表征系统非线性强度的系数,若U∈[O,2],则上式是从闭区间[-1,1]到它本身的一个非线性映射,当U→1. 40115时,周期T→∞,Logistic映射进入了混沌状态;此时输入不同的初始值,可对应一个迭代序列,即混沌序列。
Chebyshev映射定义为:
![]()
式中:k为表征系统非线性强度的系数,当k≥2时,映射处于混沌状态,将Chebyshev映射产生的混沌序列变换为独立二进制序列,可以证明其与随机二进制序列没有明显的不同。
二、交替分段相互置乱的双混沌序列图像加密算法原理
文中提出的图像加密算法在加密过程中引进了一个基于明文变化而改变的辅助密钥,由辅助密钥与初始密钥控制双混沌系统产生交替分段相互置乱的密码序列,然后将这些密码序列组合成密码矩阵对明文文件加密。其中的关键是辅助密钥和双混沌置乱序列的产生文中加密算法的加密、解密过程,如图1所示。
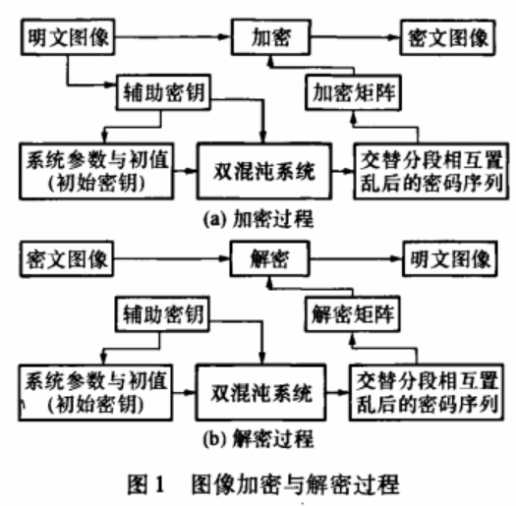
1、辅助密钥的产生
一种好的加密算法应该既要对密钥敏感,也要对明文敏感,且加密后的密文应该均匀分布在整个密文取值空间。本算法中辅助密钥起的作用有两个:
①主要作用是作为一个调制参数对初始密钥进行调制(相乘),目的是使混沌映射的初始值依赖于明文产生,整个算法对明文比较敏感,这样可以抵御差分攻击;
②辅助作用是增大主密钥空间。基于明文的辅助密钥的引入,使得系统的初始值每次都不相同.由于混沌映射的初始值(借助辅助密钥调制产生)对明文有很强的依赖作用,故本加密算法与常规算法相比,对明文有较强的敏感性。本加密算法中辅助密钥的产生借助于明文图像,由明文图像各点的像素值求和,再对256取余数,然后除以256,得到一个位于(0,1)之间的辅助密钥,正是由于辅助密钥参与加密才使得攻击者很难通过已知明文的攻击方式破译加密图像。
2、置乱数组的产生原理
文中采用Logistic与Chebyshev双混沌系统来产生交替分段相互置乱的密码序列,较好地掩盖了混沌的动力学特性,因而用常规的混沌加密分析方法较难破解密码序列。产生置乱序列的关键是置乱数组的产生,置乱数组的产生原理如图2所示。
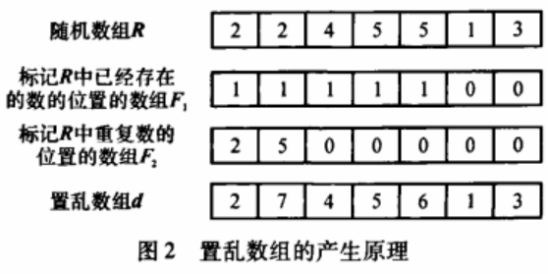
为简要说明其产生原理,假设C为混沌序列,Dc为置乱后的混沌序列,足为长度为7的且值介于[1,7]之间的一组随机数组,第1遍遍历数组足后,数组Fi用来标记足中已经存在的数的位置,例如1一5这5个数都存在,则在F1中1一5的位置均记为1,而F2用来顺序标记足中重复的数出现的位置,比如足数组中第2位重复了2,第5位重复了5,则Fz中前两位记为2和5。并设置一个计数变量y用于记录Fz中非0位的个数,对于图2,V=2;然后进行第2遍遍历,遍历F1,发现第i位不为1,则执行R(F2(v))=i操作,同时执行V=V-1的操作,经过第2遍遍历,数组R变为了置乱数组d,其值介于[1,7]之间,且各不相同。然后以数组d的值作为扰乱后数组的下标完成对原始混沌序列的置乱,即:Dc(d(i))=C(i)。
文中的置乱序列将借助上述方法产生:①由Logistic和Chebyshey两个映射在某初始条件下产生两组长度为MN的混沌序列,并将其值变换到[0,255]之间,得到两个数组L1与C1;②由另两组初始条件产生两组混沌序列,并将两组序列值分别变换到[1,MN]之间,作为随机数组,对该两组序列进行遍历,用介于[1,MN]之间但不存在于该两组序列中的值取代序列中重复存在的值,得到两个置乱数组L2与C2;③在映射关系M1(C2 (i)))=Li (i),Mz(Lz(i)) =C1 (i)的条件下产生两组密钥序列M1与M2,生成与明文图像矩阵同样大小的加密矩阵,其中奇数行由被ChebysheV映射序列C2置乱的Logistic映射序列肘,相应位赋值,偶数行由被Logistic映射序列L2置乱的Chebyshev映射序列M2相应位赋值,最终生成密码矩阵Mkey。
3、加密步骤
设A表示大小为M×N的图像,加密步骤如下:
(1)设定初值。给定Logistic系统的参数值u1、u2和初始值x0、x1,以及Chebyshev系统参数值k1、k2及初始值yo、y1。
(2)辅助密钥的生成。将明文图像A所有像素的值求和,并对256取余数,得到一个[0,255]之间的数,接着将该数除以256,得到一个(0,1)之间的辅助密钥0,辅助密钥随着明文的变化而变化:
![]()
(3)基于辅助密钥的系统初值的产生。用θr与x0、yo、x1、y1分别相乘(θr作为调制因子)。得到4个新的系统初值x0'、yo'、x1'、y1'。
(4)混沌序列L1、C1的产生,将x0',u1',yo'、k1代入Logistic映射方程与Chebyshev映射方程相应地产生两个长度为MN的混沌序列L1'、C1',序列中的值乘以一个足够大的正整数Rm,取绝对值后再对256取余数,转化为[0,255]之间的值,得到序列L1、C1:
![]()
(5)混沌序列L2'、C2'的产生,将参数u2、k2,初值膏x1',y1'分别代入Logistic系统与Chebyshev系统,产生两个长度为MN的混沌序列L2''、C2''将序列中每个值都乘以某个足够大的正整数Rm,取绝对值后再对MN取余数后加1,得到两个长度为MN并且值介于[1,MN]之间的两个序列L2'、C2'。
![]()
(6)置乱序列产生。对序列L2'、C2'从1到MN进行遍历,如果序列L2'、C2'中出现重复的数,便用1到MV之间但不存在于序列L2'、C2'中的数进行替换,得到两个值互不相等且分布在[1,MN]之间的序列L2'、C2',这两个序列为置乱序列,用于对序列C1、L1进行置乱,置乱数组L2、C2与数组L1、C1之间的映射关系为:M1(C2(i))=L1(i),M2(L2(i))=C1 (i),即通过Chebyshev映射序列置乱Logistic映射序列,由Logistic映射序列置乱Chebyshey映射序列。
(7)加密矩阵生成,将序列M1、M2共同组成密码序列瓯,以N为单位轮流截取M1、M2中相应位置的值,这些位置与瓯中的位置相对应,然后将这些值置于Sk中的对应位置,Sk长度为MN,最终将瓯按行优先的原则构成加密矩阵MKEY,其大小与明文图像大小相同,即其中奇数行是由M1相应位赋值,偶数行是由M2相应位赋值。将明文矩阵A与密文矩阵MKE/r异或以后得到加密后的矩阵B。
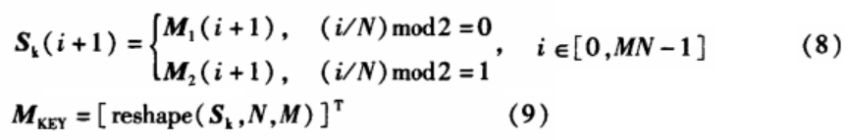
式中:i/N为i除以N的整数商,reshape()为Matlab中的矩阵成形函数。
解密过程是加密的逆过程。
三、加密算法仿真分析
通常图像信息存储和传输的流程为:原始图像一压缩(有损或无损压缩算法)一加密一解密—解压缩。从信息论的角度来看,图像文件加密后,由于相邻像素点间相关性的破坏,很难再进行压缩,难获得高压缩率,这样压缩效果并不好,因此一般的过程是先压缩再加密,解密过程是先解密后解压缩,文中利用Matlab 7.0软件,结合上述算法,先进行无压缩仿真,再进行有损压缩明文后仿真.在系统参数u1 =1. 911158,u2=1. 9275723,k1=4.775 865,k2 =5,初始值x0=0.588 234,x1=0.362 754,y0=o.627491.y1=0.322356时,对一幅256 ×256的灰度图像“camenunan.tif”进行了加密解密仿真实验,结果见图3(a)一(c)。
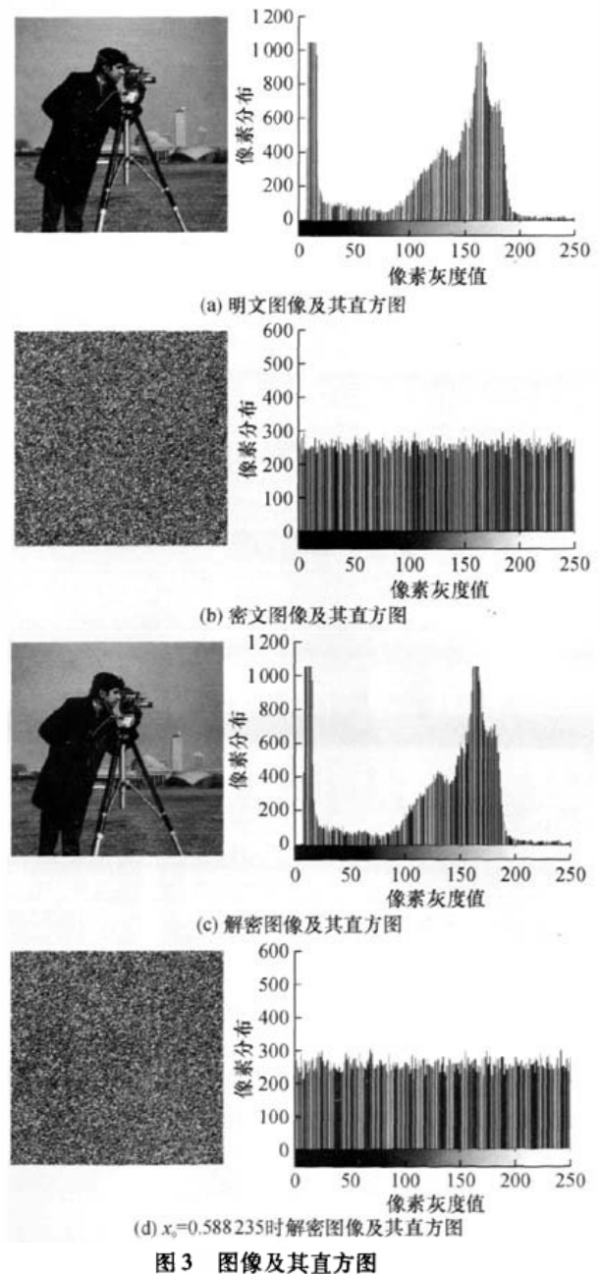
由图3(a)、(b)可见,明文图像的像素值数目分布是不均匀的,而密文图像的像素值在数目上呈现均匀分布,掩盖了加密前的分布规律,从而增大了破泽者的工作量和难度,使得密文具有良好的抵抗统计分析攻击的能力;由图3(c)、(d)可见,密钥的微小差别将导致密图完全不能解密,表明加密算法对初始密钥有较强的敏感性,图4(a)为密钥初始值x0分别为0.588235与0.588 234时,其他初始条件不变的情况下得到的加密图像的差图,如果两次加密的密图像素值完全相同,差图显示出来将是一幅完全黑色的图像(即所有像素点的值都是0)。

而本图像加密算法差图显示的却是值分布在[0,255]之间的一个矩阵,密钥的微小改变导致了加密图像效果很大的不同,再次证明了本加密算法对密钥的较强敏感性;图4(b)为改变明文图像中一个点A15,使其灰度值从158变到159,其他初始条件不变的情况下得到的加密图像的差图,与图4(a)相似,可见明文仅一个像素的微小差别就导致了加密效果的截然不同,表明本加密算法对明文图像也具有较强的敏感性;其中图5为用Pic manager软件压缩过后的明文图像(原始图像为63. 7kB,压缩后为12. 8kB),用本算法加密后的图像以及正确解密后的压缩图像,由图5可知本算法适用于压缩后的图像加密传输。

由图3、4可知,本图像加密算法对密钥和明文均有较好的敏感性,因而能有效抵抗基于对明文图像做微小修改的差分攻击方法。
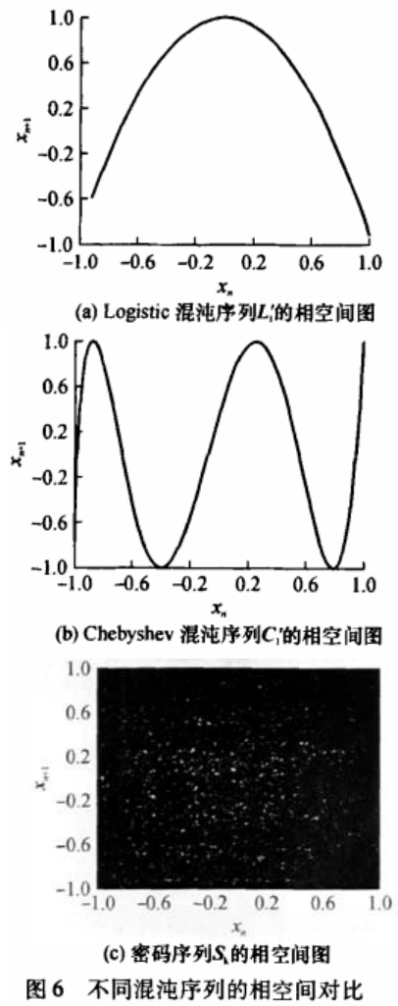
图6为混沌序列相空间图,由图6(c)可知,密码序列Sk完全掩盖了原混沌序列的相空间轨迹,其混沌动力学行为被很好地遮掩。因而依赖于所截获的信号的混沌动力学行为的解密分析方法失效,攻击者无法进行相空间重构,从而无法恢复出混沌系统的表达式。
四、加密算法统计特性分析
在明文图像和密文图像中随机选取20个像素点,垂直方向10个,水平方向10个,通过以下方法计算明文与密文相邻像素点间的相关系数rry,计算公式如下:
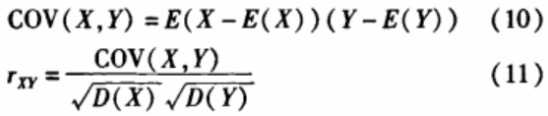
式中:x、y表示两个相邻像素的灰度值,在实际测试中采用如下离散化的计算公式:
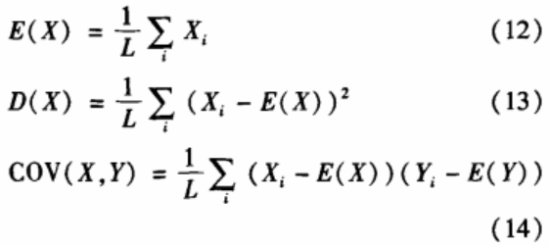
式中:COV(.)表示协方差;E(.)表示期望;D(.)表示方差;二表示数据长度,通过计算,得到明文图像相邻像素点的相关系数矩阵(见表1)和密文图像的相邻像素点的相关系数矩阵(见表2)。由表1、2可以看出,加密前的图像像素值间具有较强的相关性,经过加密过后,这种相关性被破坏。
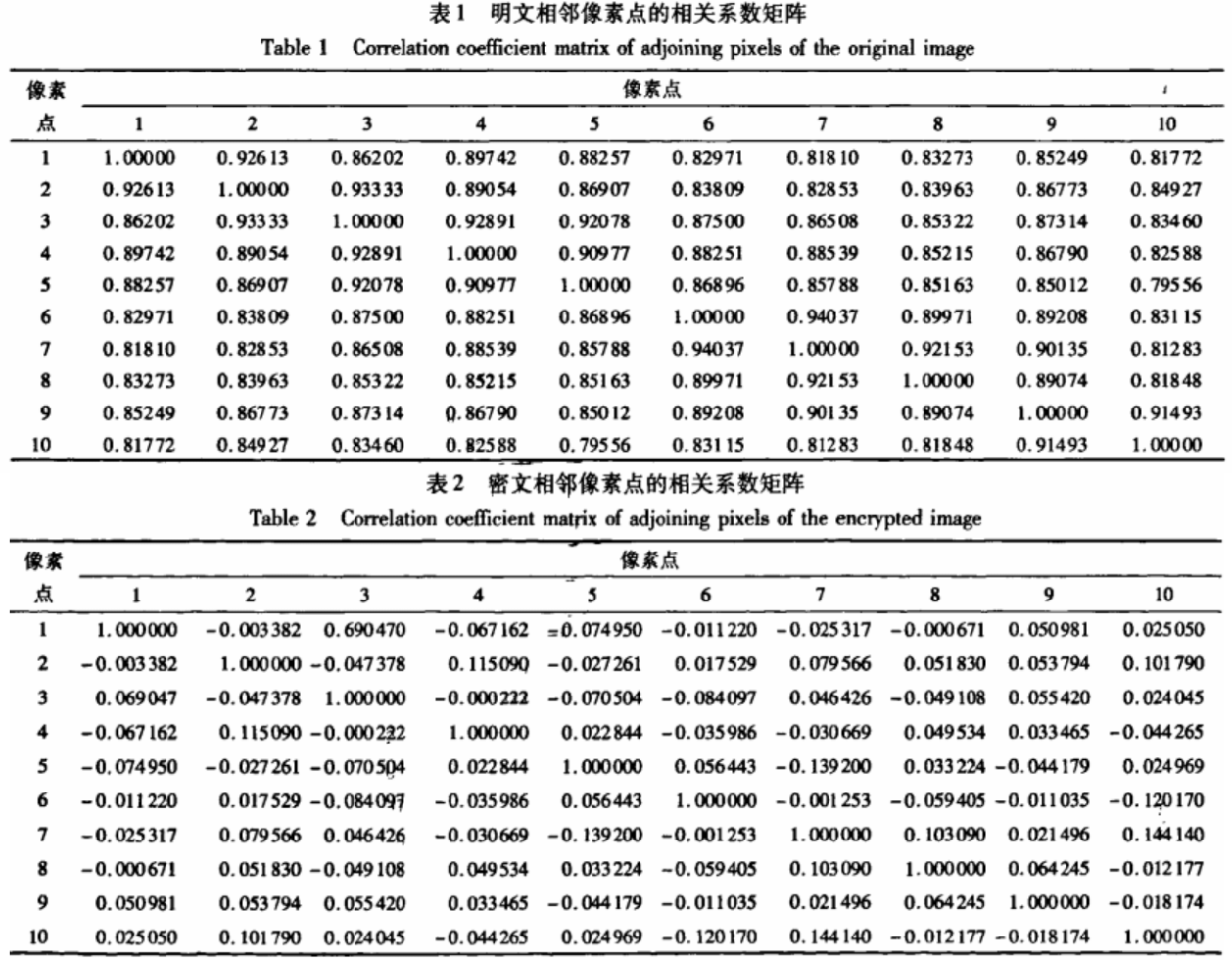
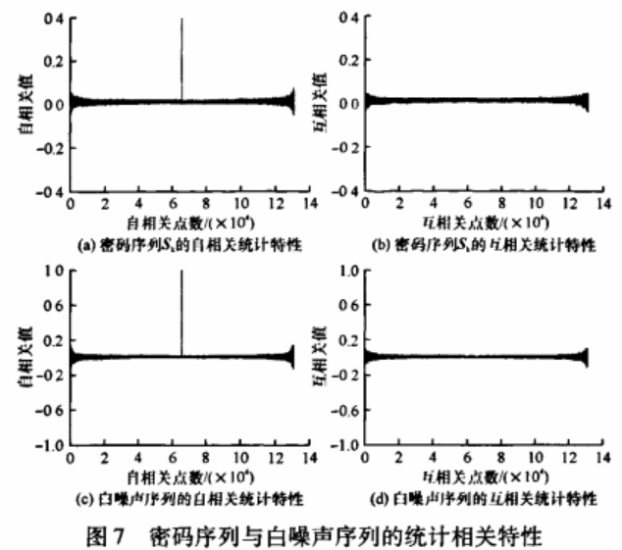
图7(a)、(b)分别是交替分段相互置乱的密码序列Sk的自相关、互相关特性,平均分布的的白噪声序列的自相关、互相关特性分别如图7(c)、(d)所示。由图7可见,二者的特点相似,表明采用Logistic与Chebyshev双混沌系统产生的交替分段相互置乱的密码序列Sk符合平均分布,因而文中加密算法能很好地隐藏明文的信息。
小知识之密钥
密钥是一种参数,它是在明文转换为密文或将密文转换为明文的算法中输入的数据。











