admin 基于Logistic映射和正弦混沌映射的交替混沌加密算法通过Logistic映射和正弦混沌映射两个混沌源产生两个不同的混沌序列，采用一定的加密算法交替对明文流加密，进一步增强了混沌序列的随机性，扩充了密钥空间，能有效的防止穷举攻击和频率攻击等多种攻击手段，具有良好的安全性。
一、混沌系统基本特性
1、混沌序列的特性及在加密领域中的应用
混沌是自然界和人类社会普遍存在的一种现象。混沌理论是现代科学与现代技术，特别是计算机技术相结合的产物。自从Lorenz于1963年在大气科学的研究中首先提出了混沌的概念后，混沌在各个领域都得到了不同程度的运用。我们首先引用一个被文献广泛认可的混沌概念：
定义1：设X为一个度量空间，f：x→x称为在X上是混沌的，如果满足：
（1）f对初始条件有敏感依赖性：如存在δ>0对任何x∈X和x的任何邻域N，存在y∈N和自然数n>0，使得d(fn(x)，fn(y))>δ；
（2）f是拓扑传递的：如对任何一对开集u，v⊂x，存在k>0，使得fk(U)∩y≠φ：
（3）周期点在V中稠密。
混沌系统具有以下明显的特性：
（1）随机性。只要选取的参数在混沌区，方程所输出的序列即为混沌的。
（2）确定性。混沌是由确定性方程产生的，只要方程参数和初值确定就可以重现混沌现象，尽管{Xi}出现随机的性质，但它可由确定性方程给定，即{ Xi+1）可由{Xi}导出。
（3）遍历性。混沌运动的遍历性是指混沌变量能在一定范围内按其一定的规律不重复地遍历所有状态。
（4）对初值的敏感性。初值（xo）的微小的差异，{Xn｝将有很大的差异。
混沌系统所具有的这些基本特性恰好能够满足Shannon在他的经典论文中所提出的密码系统设计的两个基本原则——扩散和混淆原则。信息论的奠基人，美国数学家Shannon指出：若能以某种方式产生一随机序列，这一序列由密钥所确定，任何的输入值的一个微小变化对输出都具有相当大的影响，则利用这样的序列就可以进行加密。混沌系统恰恰符合这种要求。
2、Logistic映射的性质
Logistic映射是最典型的，也是研究的最广泛的动力系统，其定义如下：
其中：0≤μ≤4为分叉参数。混沌动力学的研究表明，当3. 5699456---<μ≤4时，Logistic映射处于混沌状态，即产生的序列（Xk，k=0，1，2，3“t）是非周期的，不收敛的，且对初始值非常敏感。当μ=4时，该映射是满射，产生的混沌序列在区间(0，1)上具有遍历性。这点正是Logistic映射用于密码学的优势。
3、正弦迭代混沌系统
其中，l<b∈R，系统初值x(0)∈R，且0<x(0)<1，由式②产生的混沌系统的Lyapunov指数是1nb>0，满足混沌化的条件。
二、混沌加密解密的基本原理
1、混沌序列密码系统
混沌序列密码系统的加密端和解密端是两个独立的、完全相同的混沌系统，两系统闻不存在耦合关系。明文信息在加密端加密后直接发往解密端，解密端可以在全部接收后再解密，也可以利用其它技术如线程同步等建立同步关系后进行实时解密。此方法的安全性依赖于混沌信号的超长周期、类随机性和混沌系统对初始状态、系统参数的敏感性。混沌序列密码加密方法灵活
多变，可以充分利用混沌信号的特性构造复杂的加密函数。
2、混沌序列的数字离散化
混沌序列加密的安全性主要依赖于混沌密钥流，在混沌加密系统中，将混沌系统产生的伪随机序列作为密钥流(Logistic映射产生Xi密钥流，正弦混沌映射产生Yi密钥流)与明文数据流按位运算，从而产生密文数据流。当混沌系统在计算机上实现时，计算精度、所采用的机器都可能影响有限精度混沌系统的展终结果，数字化混沌系统与理想的实值混沌系统在动力学特性上存在相当大的差异，为了使混沌序列离散化结果保持最大可能的随机性，采取下列方法：
首先，为了得到更好的随机序列，Logistic映射和正弦混沌映射均迭代n次后取密钥流。参考大量实验结果并兼顾加密速度的要求n取500。
其次，经迭代生成的实数序列不宜直接用于加密，而且理论研究表明：这种无误差的平凡混沌加密方法是可破解的。而且混沌加密过程是指，将得到类随机流只经过简单初等交换，直接作用于明文的加密过程。可以设想一部分窃密者足可以通过别的途径得到一些与密文相应的明文的，而且可以猜测出加密算法的大致过程，他们可以有选择对密文进行处理。对应这一类加密
者的破解，当他们得到连续一段的带有相应的明文的密文，且密文长度满足一定条件，如上所指出的混沌加密过程则可能面临崩溃性的灾难。
由于加密的是数字量，所以将这个由实数构成的序列映射度成由整数构成的伪随机序列来充当加密密钥。常用的一种映射方法是选取Xi或Yi小数点后的儿位有效数字构成整数。选择有效位的方式也可以作为密码，有利于提高抗选择明文攻击的能力和增加密钥空间。
3、混沌加密密钥的产生
由于初始参数不同，混沌系统可产生不同的混沌序列，因此初始参数可作为密钥；混沌系统对初始值异常敏感，即使两个完全相同的混沌系统对稍有差异的初值会产生完全不同的序列，因此初值可作为密钥；在混沌序列离散化的过程中选择有效位的方式也可以作为密码；由于采用Logistic映射和正弦混沌映射产生两个不同的混沌序列Xi和Yi，交替对明文流加密K次，因此参数K也可以作为密码。实际应用时可根据具体情况有选择的使用上述参数。
三、混沌加密算法实现
选取Logistic映射Xn+1=μXn(1一Xn），取参数μ=4，该映射为满射，具有良好的混沌特性：选取正弦混沌映射，
，参数作为初始密钥一部分。采用上述两个混沌映射产生的混沌序列Xn和Yn交替对明文流加密，设置一逻辑型变量Enisl(Encryption is Logistic)，当Enisl值为True时，采用Logistic映射产生的混沌序列Xn加密8次，当Enisl值为False时，采用正弦混沌映射产生的混沌映射Yn加密8次。Xn序列量化函数采用选取小数点后4、5、6位有效数字构成整数，对256取余，Yn序列量化函数采用选取小数点后7。8、9位有效数字构成整数，对256取余。在具体程序实现时选取小数点后有效数字的方式可以由用户灵活指定，这样进一步拓宽了密钥空间。具体算法步骤如下：
（1）输入Logistic映射初值x0和正弦混沌映射初值y0，参数b。
（2）Logistic映射和正弦混沌映射分别迭代500次。
（3）判断加密完成否，若完成退出，否则转(4)。
（4）读取明文串。
（5）运行混沌发生器，判断Enisl值，若为True，则迭代Logistic映射8次，如果迭代值未在区间(0.2，0.8)之问则舍弃继续迭代，因为Logistic映射的统计分布在两端具有奇异性，直到得到8个迭代数据，运行量化函数（采用选取小数点后4、5、6位有效数字构成整数，对256取余），否则达代正弦混沌映射8次运行量化函数（选取小数点后7、8、9位有效数字构成整数，对256取余）。
（6）将混沌密钥与明文位串进行异或运算，转(3)加密算法流程图如图1所示：解密时采用相同的算法与密文异或即可。
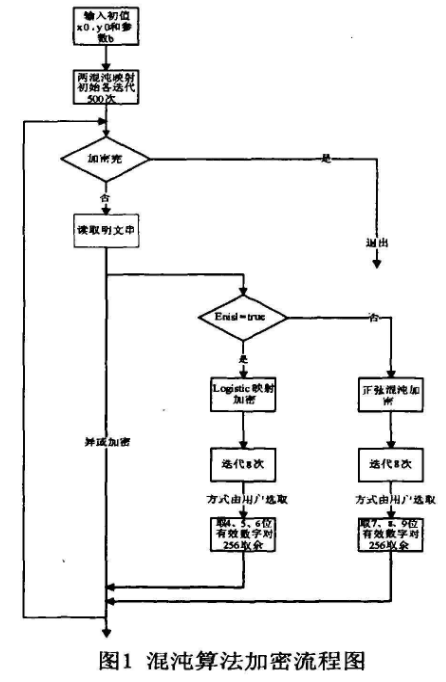
四、加密算法仿真与分析
选取Logistic映射初值xo =0. 4019，μ=4。选取正弦混沌映射初值Yo =0. 6813．b=3. 9125在计算机上仿真结果如下：
图(a)是原始图像，图(b)为加密后的图像文件，图像文件加密精辟变得杂乱无章，图(c)为正确解密后的图像文件，和原始图像毫无差异，而图(d)是采用错误密钥解的密后的图像，仅将解密密钥x，变成0.4017，和正确解密密钥0.4019差别很小，其它数值不变，但无法正确还原原始图像，可见该加密算法对初值的极度敏感性。
加密算法特性分析：
（1）由仿真实验可知该混沌加密xj初值和参数具有极度敏感性，因此在可以提供极大的参数空间。同时在混沌序列离散化的过程巾选择有效位的方式和迭代次数也可以作为密钥，进一步拓宽了参数空间，用户可根据实际情况灵活选择。采用穷举攻击几乎是不可能的。
（2）采用Logistic映射和正弦混沌映射两个混沌源产生两个不同的混沌序列，交替对明文流加密，进一步增强了混沌序列的随机性。特别是Logistic映射舍弃了区间(0.2，0.8)之外的数据，数据分布更均匀．数值分布上不符合概率统计学原理，得不到一个稳定的概率分布特征，可以更加有效防范频率分析攻击，因此统计分析的攻击方法对该算法也无用武之地。
（3）混沌加密属于流密码的范畴，加密仅是简单的异或运算，加密速度快，特别适合多媒体数据和实时性要求比较高的加密场合。
（4）混沌序列加密的安全性主要依赖混沌信号发生器产生混沌信号序列流的随机性。从理论上讲，混沌序列流是随机的，符合密码学Ⅳ一次一密一的加密要求。但由于受计算机精度的限制，混沌产生的类随机流无法达到数学上的理想状态，福特(FordJ．)指出，混沌只是数学上所要求的无限观测精度与物理系统所提供的有限精度之间的矛盾。
小知识之拓扑
拓扑学的英文名是Topology，直译是地志学，也就是和研究地形、地貌相类似的有关学科。几何拓扑学是十九世纪形成的一门数学分支，它属于几何学的范畴。有关拓扑学的一些内容早在十八世纪就出现了。那时候发现一些孤立的问题，后来在拓扑学的形成中占着重要的地位。
