目前的绝大多数加密算法是把图像文件加密成客户无密钥就不能理解的数据,但在某些诸如视频点播、音频点播等应用中,图像或者声音可能在传输前要降质处理,以便即使其中有降质,客户仍能理解,他们在观看或试听之后决定是否购买更高质量的版本。基于此,我们提出一种加密质量可以控制、与JPEG2000标准兼容、支持细粒度可伸缩的图像小波近似系数混沌加密算法。
一、混沌映射
1、非线性映射
设Tn(x)是定义在区间I=[-1,1]上的非线性映射:
![]()
前三个非线性映射分别可表为:![]() 而其它映射均可由式(2)递推得到:
而其它映射均可由式(2)递推得到:
![]()
对于n∈N,n≥2,x∈[-1,1],所有Tn(x)都是混沌的,其混沌动力系统的轨迹可由式(3)迭代得到:
![]()
且其轨迹分布具有概率密度函数:
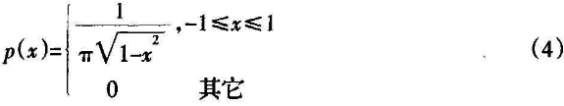
为直观验证映射Tn(X)的混沌性质,取n=5,以随机选取的x0∈(0,1)为初始值,按式(5)生成序列{Xk|k=1,2,3,…,10000}。
![]()
发现其轨迹随机地分布在区间[-1,1]上(如图1(a));将[-1,1]等分为50个子区问后,统计得出序列在各子区间出现的频数分布并不均匀(如图1(c))。
用于密码系统的最理想的混沌动力系统应该是服从均匀分布的,因此,基于Tn(x),定义映射G(x):
![]()
显然,yk∈[0,1]。
类似地,取n=5,按式(6)生成随机序列{yk|k=1,2,3,...,1 0001},直观发现映射G(x)比Tn(x)具有更好的混沌性质(如图1所示):其轨迹随机分布在区间[0,1](如图1(b));当将[0,1]等分为50个子区问时,统计得出序列在各子区间出现的频数分布是均匀的(如图1(c))。
定理1G(x)是混沌的。
证明由于Tn(x)的值域正好是严格单调递增函数arcsin(x)的主值区问,从而G(x)是从[-1,1]到[0,1]上严格单调递增的一一映射,因此,由Tn(x)的混沌性知G(x)也是混沌的。
定理2由G(x)生成的混沌序列{yk|k=1,2,3,...}服从[0,1]上的均匀分布U(O,1)。
证明_y∈[0,1],混沌序列{yk|k=1,2,3,...}的分布函数为:
![]()
可见,混沌映射G(x)的轨迹服从[0,1]的均匀分布U(0,1),且具有概率密度函数:
![]()
2、Logistic映射
众所周知,Logistic混沌映射具有如下形式:
![]()
其中,3.5699456<μ≤4,且由式(9)容易得到如下结论。
定理3对给定正整数k由式(9)生成的混沌序列{zk|k=1,2,3,...}满足:(1)_z0∈[0,1]_zk∈[0,1](2)若zk=1或zk=0,则zk+i=0,i=1,2,3,…;(3)若μ=4,zk=1/2,则zk+i=0,i=1,2,3,…。
由此,可得到如下定理。
定理4若3.569 945 6<μ<4,zo≠0,zo≠1,则由式(9)生成混沌序列{zk|k=1,2,3,...}。
证明反证法。若有正整数K,使得zx=0,zx-i=。显然,由zo≠0,zo≠1知,K>1,且:
![]()
与3.569 945 6<μ<4矛盾。故zk≠0,k=1,2,3,…。
二、图像加密算法
现代密码学要求,图像加密技术要把待传输的图像看作明文,在密钥控制下,通过加密算法实现图像数据的保密通信。这种加密机制的设汁思想是加密算法可以公开,通信的保密性完
全依赖于密钥的保密性。为此,本文设计的加密算法对用户可以公开,图像安全性和视觉效果的控制依赖于混沌动力系统的安全性、随机性及密钥安全性。
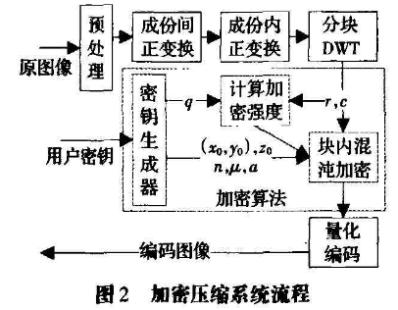
该图像加密算法的流程(如图2中方框内所标注“加密算法”)是JPEG2(XX)编码算法的完整过程的组成部分,本文重点叙述小波变换后、压缩编码前的加密算法(解密是加密的逆过程):
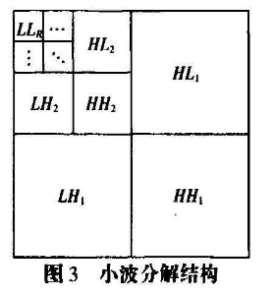
步骤1对图像块进行尺层小波分解(如图3)。
步篡2生成加密方案中使用的密钥参数:q,n,xo,yo,μ,zo,a,使得3.569 945 6<μ<4, 0.1≤a≤0.5。
步骤3计算加密数据量。用式(11)表示的近似系数加密量算法模型控制加密图像的视觉质量:
![]()
其中,r,c为子带LLR的行列数,g为保持原图像质量的百分比。q越大,视觉效果越好,但保密度越低。
步骤4利用混沌映射生成加密像素的随机位置集P=PK=(XK,yk)|1≤k≤m)。将给x0,y0,n代入式(3)计算,并用式(6)进行均匀化处理得序列{Xk| 1≤k≤m}和{yk|1≤k≤m},再计算:
![]()
然后,取P={pk(xk’,yk’)|1≤k≤m}。
步骤5按式(9)生成混沌序列{zk|zk≠0,l≤k≤m},按下式对近似系数加密:
![]()
其中,pk∈P,而0.1≤a≤0.5为近似系数凋节深度控制系数。则可按下式对近似系数解密:
![]()
三、密钥生成算法
加密方案中使用的密钥是—个由7个参数构成的向量,这些参数包括:视觉质量q,混沌映射的参数n,μ和初值x0,y0,zo,加密系数a,它们是浮点数或整数。而用户输入的密钥Ku是7
个字节的串,可以看着一个比特序列,因此这里给出—个把Ku变成7个所要参数的如下变换:
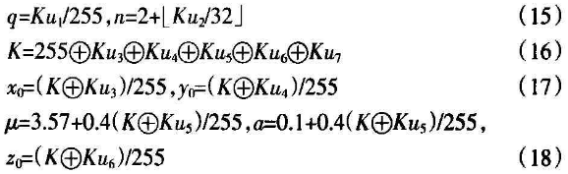
显然,3.569 945 6<μ<4,0.1≤a≤0.5。
四、加密算法有效性分析
1、复杂性分析
加密方案以小波近似系数为加密明文,数据量为原图像的2-2r,呈指数级减少;密钥生成算法是几次一劳永逸的代数运算;加密算法的复杂性仅为0(n)(设n为近似系数个数,远少于原图像数据量)。由于计算规模较小,所以运算速度非常快,相对于复杂的压缩编码运算,这里的计算可看作是一步简单操作。
2、安全性分析
用户输入的是7字节密钥串,密钥空问的不同密钥串的个数为256=7.205 8e+016。如果采用穷举法对算法实施攻击,假设一台超高速计算机每秒可以试100亿个密钥(解密速率要达到这个数量级儿乎是不可能的),要穷尽所有密钥也要83天时间,这在实时性要求较高的保密通信系统中,即使找到了加密密钥,由于其滞后时问太多,也已经失去了攻击的价值。
可见,密钥空间已经足够大了。
同时,混沌系统的伪随机性、轨迹的均匀分布性使得被图像文件加密的数据位置具有不可预见性;混沌系统的初值敏感性确保了加密算法对密钥的敏感依赖性。
五、实验验证与效果
为测试该图像加密算法的有效性,用Matjab工具编程测试了来自通用测试图像库的多幅图像,得到的结论非常一致。表1中给出了对其中的512x512的Lena和Baboon灰度图像进行加密实验的测试结果数据。其中,小波滤波器为Haar小波,分解层数R=3;原图像与加密生成的图像的峰值信噪比(PSNR)是按式(19)计算的(式中的而,w分别为图像的高度和宽度,Py,Py‘分别为原图像和加密图像的像素值);通过密钥确定的n=5,μ=4,a=0.5。
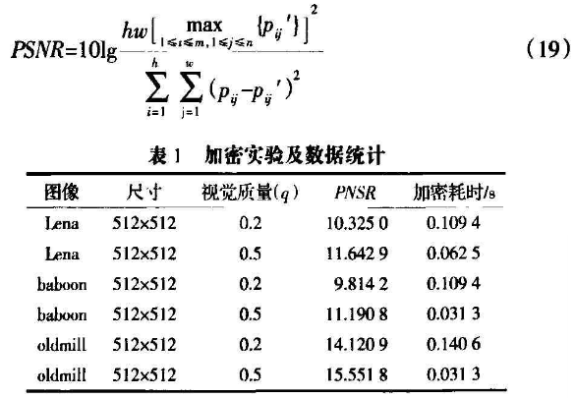
从表中数据可见,幽像质量越高,由于被加密改变的像素就越少,所以相应的PSNR就越大,加密耗时也就越少。在图4中给出了Lena图像加/解密实验的效果对比图,达到了预期的质量控制效果。

此外,加密方案是嵌入可伸缩的JPEG2000编码方案的一个步骤,由于是通过对最粗一层近似系数进行的随机加密,即未对细节系数加密,因此,加密后的码流仍保持了细粒度可伸缩性,不可信赖方等仍可不对码流解密就商接作任意分解层的细节系数的截断,从而满足了对任何分解尺度的近似图像的浏览与解码需求。
加密方案和实验结果表明,本文提出的混沌加密算法实现了加密质量可以控制、与JPEG2000标准兼容、支持细粒度可伸缩、安全与高效的算法目标,可以应用到静态图像、视频图像帧的加密编码系统。
小知识之JPEG 2000
JPEG 2000是基于小波变换的图像压缩标准,由Joint Photographic Experts Group组织创建和维护。JPEG 2000通常被认为是未来取代JPEG(基于离散余弦变换)的下一代图像压缩标准。JPEG 2000文件的副档名通常为。jp2,MIME类型是image/jp2。











