加密算法之基于观测器同步的超混沌系统加密

在混沌通信系统中，超混沌系统同步技术越来越受到重视。为此我们提出了一种基于观测器的超混沌同步加密算法应用于数字签名技术，这样既克服了传统的RSA和DSA加密算法中复杂的模运算，又能提供很好的保密性和不可抵赖性。

一、离散混沌系统同步原理

基于观测器，用一个标量信号同步离散混沌系统的方法，其基本原理如下：

离散混沌系统的状态方程和输出方程的一般表达式描述为：

b∈Rn和c∈Rn是常数矢量，f：Rn →R是非线性函数，y(k)是标量同步输出信号，K∈Rn是设计参数。当给定驱动系统式(1)，基于观测器的方法能用观察量式(2)中所包含的状态信息重构出响应系统的状态，重构的响应系统一般表达式为：

其中观测量y(k)的预测由：

给出定义同步误差e(k)=x(k)一x'(k)，产生的系统误差动力学由下列线性时变系统描述：

如果

是一个满秩的矩阵，只要选择适当的K使得[A_bKT]的所有特征值为零，那么误差动力学式(5)将在步迭代后准确为零。

此方法的优点在于对于一个m维离散混沌系统而言，只需m步就可达到完全同步；混沌同步在一定程度上具有自保持性。其理论体系是严格、系统的，而且不要求计算Lyapunov指数，甚至不要求驱动系统和响应系统的初始条件一定要属于相同的吸引区。

二、超混沌广义Henon映射的同步

有专家设计了理论上可无阻维的广义：

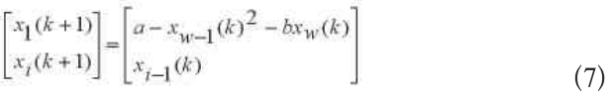
加密算法之基于观测器同步的超混沌系统

式中：i=2,3...w，a>o,b>0，x∈Rw为维数，a和b为控制参数。

当w=2时，该系统即为著名的Henon映射。

Richter详细计算了当固定控制参数a=1.76，b=0.1时的李氏指数，假设L是正的李氏指数的个数，当w从2到10变化时，有如下线性的对应关系L=w-1。换句话说，就是当w>2时，该系统为超混沌。

本文采用四维广义Henon映射，描述如下：

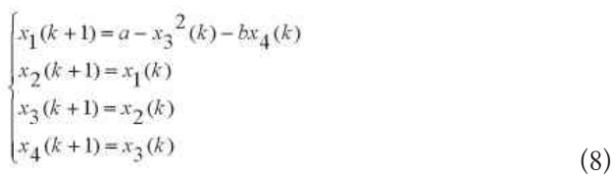
加密算法之基于观测器同步的超混沌系统"

其中，o <|b|<1，1.54<a<2，系统具有三个正的Lyapunov指数。当a=1.76，b=0.1，对于初始条件下X1(1) =1，X2(1) =1，X3(1) =1，X4(1) =1，系统呈现出超混沌行为，其空间相图如图1所示。依次为X1 - X2 - X3相图，X1-X2-X4相图，X1 -X3-X4相图，X2-X3 -X4相图。

加密算法之基于观测器同步的超混沌系统

超混沌广义Henon映射写成式(1)的形式，则：

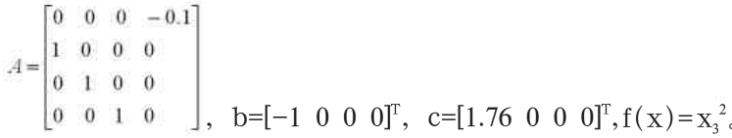
加密算法之基于观测器同步的超混沌系统

容易证明从超混沌广义Henon映射式(8)获得的矩阵式(6)是满秩的。选择：

为同步输出信号，通过选择适当的K使[A-bKT]的特征值为零，系统就能达到同步。这里，通过极点配置法选择增益K为[000 0.1]，将两个待同步的超混沌广义Henon映射的初始条僻分别选择为X1(1)=1，X2(1)=1，X3(1)=1，X4(1)=1和。经过计算机仿真，可以清楚地看到，经过四步迭代后，从不同的初始点开始的两个超混沌广义Henon映射达到了精确同步，如图2所示。其中，。

加密算法之基于观测器同步的超混沌系统

三、超混沌同步加密

采用非线性状态观测器设计技术进行加密，系统框图如图3所示。

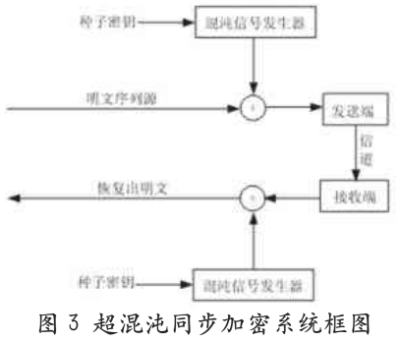
加密算法之基于观测器同步的超混沌系统

本文中采用典型的一维Logistic映射作为混沌信号发生器产生混沌序列，Logistic映射是一个离散混沌系统，它的映射关系为：

当xk∈[0-1]，λ∈(3.569945.4)时，系统处于混沌状态。设定系统初值和参数，代入混沌映射公式即可得到一系列混沌实数序列。由于系统初值和参数可以在给定范围内任意取值，故可以产生大量初值和参数组合，从而有较大的密钥空间，增强了保密性。针对本文仿真采用的文本加密，输入输出均为字符的ASCⅡ码，即0，1码流，所以对于混沌实数序列采取量化处理，即规定：

由混沌序列生成新的码字，与输入的明文码字进行异或处理，即可得到待传输的信号。

设计的超混沌加密系统其发送端一般表达式为：

接收端一般表达式为：

定义状态同步误差，使得：

只要适当地选择K，使得[A-bKI]的所有特征值为零，那么发送端和接收端在迭代有限步之后就能达到同步。从而得到所传输的序列s(k)，从而最终恢复出明文。

四、实验结果与分析

为了验证此加密系统是否可行，对以下文本文件加密，即选择明文如下：

Welcome to Yanshan Umversity!

其对应的AscⅡ码(240位)为：

01010111 01100101 01101 100 01100011 01101111 _01 1 01 1 01 01 1 001 01 00100000 01110100 01101111 _00100000 0101 1001 01100001 01101110 01110011 _01 101000 01 100001 01 101 1 10 00100000 01010101 _01 1 01 1 1 0 01 1 01 001 01 1 1 01 1 0 01 1 001 01 01 1 1 001 0 _01 11001 1 01 101001 011 10100 01 1 11001 0100001

设定初值分别为3.8和0.1，通过Logistic映射产生混沌序列X1, X2, X3, X4, X5，由图2可知，超混沌同步系统经过四步迭代后方能达到同步，故在此选取Logistic映射中的X6， X7，...X245，共240个，保证超混沌系统可以达到同步，从而能够正确恢复明文。将其量化然后与明文序列相异或所得s(k)为：

10001000 00001 1 10 00010010 101 1 1 100 1 101 1000 _11010110 00111110 1 1001010 10100010 10010100 _10001 1 1 1 10000100 00011110 1 1 01 01 00 1 1 0001 1 0 _000001 10 1 1001 1 10 101 10100 1 1 1 10101 10000010 _1 101001 1 10000100 10100000 1 1010010 101001 1 1 _0001 1 100 00011 100 0001 11 1 1 00000010 1 11 10100

将发送端和接收端的初始条件分别选择为：

X1(1)=1, X2(1)=1, X3(1)=1, X4(1)=1和，将s(k)在无任何噪声和干扰的信道中进行传输，结果显示基于状态观测器的超混沌广义Henon映射同步加密方法能准确恢复发送端调制的s(k)，发送端和接收端达到完全同步。接收端得到的序列如图4所示。

加密算法之基于观测器同步的超混沌系统