基于数字图像加密设计的两个基本原则是置乱和扩散,一般的加密算法针对于图像分别单独进行置乱和扩散,而我们提出一种两者相结合同步实现加密的算法,即基于置乱扩散同步实现的图像加密算法。
一、混沌序列的控制和产生
1、一维混沌系统Ulam-von Neuman映射
混沌系统是确定性的非线性系统在一定条件下的一种不可预测的类似随机运动的行为.Ulamvon Neuman映射就是一类常见的具有混沌运动特性的映射,它表示为:
![]()
在此映射中没有可变的系统参数,可改变的只是系统演化的初值。
2、二维混沌系统Logistic映射
Logistic映射是一个非常简单且被广泛研究的一维离散时间非线性动力系统,定义如下:
![]()
善乓中Xn∈(0,1)。当3.569 9456...<μ≤4时,Logistic映射处于混沌状态。
一维混沌系统虽然有着形式简单、产生混沌时序时间短等优点,但其缺陷是密钥空间太小,有时候安全性难以保障.而高维混沌系统不仅具有一维混沌系统的特性,同时具有更大的密钥空间,因此能提高加密系统的抗破译强度,且图像数据在处理时大多是存放于二维矩阵中,因此采用二维混沌系统来加密图像数据更有利于提高加密速度。如可采用具有一次耦合项形式的二维Logistic映射:
![]()
其动力学行为由控制参数μ1,μ2,γ决定,当其工作于混沌状态时,生成的迭代序列与一维Logistic映射类似,且具有更高的伪随机性。
3、一维控制二维产生混沌序列
混沌序列的产生来源于计算机的实现,但是计算机的截断误差会一定程度上降低原有混沌的特殊性质,对一般的混沌序列分析发现其均匀性并不是很好,因此随机性会降低。为了增强混沌序列的随机性,本文设计了两个混沌系统,用UlamvonNeuman映射控制二维Logistic映射产生混沌序列,这样在一定程度上增强了随机性,而且会扩大密钥空间,参见图1上半部分。(1)式产生的序列,在大于0和小于0两个区间上,概率大概各为1/2,所以(2)式中两个方程迭代次数概率大概也各为1/2。
二、置乱和扩散同步实现的图像加密算法
首先针对于一个m行n列的图像矩阵Mm×n,按照某种扫描方式确定对图像加密的顺序,常用的有光栅扫描NW→SE(SE→NW),之字形Zig-Zag扫描等。设图像某处像素值的坐标为(x,y),先对其置乱,再对其扩散。
置乱过程:一维控制二维产生的两个混沌序列,变为大小为m×n的两个二维矩阵z1和z2。在(x,y)处,计算:
![]()
其中fix()为向0方向取整。然后将M(x,y)和M(a,b)互换。
扩散过程采用下式:
![]()
其中Vi为从抽取混沌系统(1)产生的迭代序列中处理得到Ⅵ= fix(wiL),己为像素灰度级数,Ii为扩散前的像素值,G为扩散后的像素值,C为一密钥。加密算法流程图如图1。
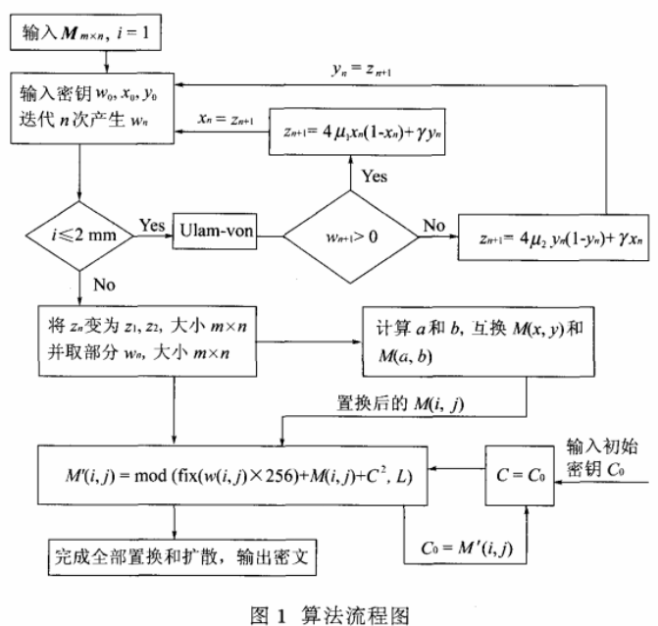
加密算法步骤如下:
步骤1原灰度图像以二维矩阵Mm×n存放;
步骤2输入密钥w0.迭代方程(1)迭代n次(n>1000),再次产生初始值;
步骤3将步骤2产生的初始值再次代入(1)式,得到Wi+1,并输入密钥zo,珈,判断若Wi+1>0。
用(3)式中的第一个方程迭代,否则用第二个方程,共进行2mn次迭代;
步骤4将得到的序列Zn变为z1和z2,大小为m×n的二维矩阵;
步骤5按某种扫描方式,再依照上述置乱过程提到的方法,对坐标为(x,y)的像素值,计算a和b,互换M(x,y)和M(a,b),同时再用(4)式对其扩散;
步骤6完成全部置乱扩散,输出密文M'm×n。
文件解密过程为文件加密过程的逆过程。
三、仿真试验分析
1、加密效果
使用MATLAB 7.8.O(R2009a)软件,利用本文的加密算法对Lena灰度图像文件加密,效果如图2。
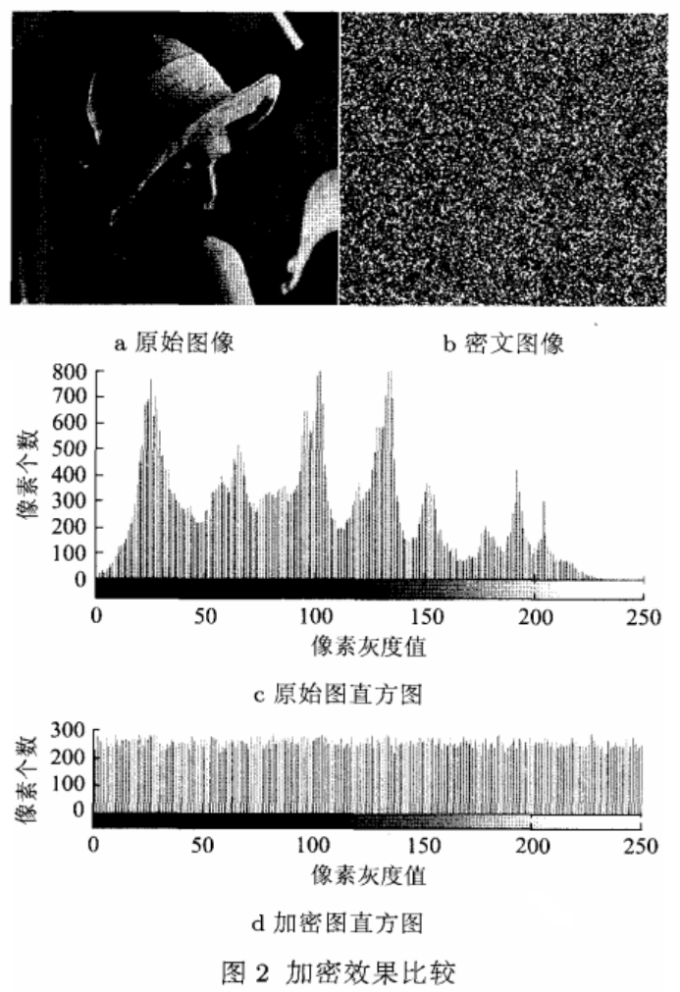
从图2中加密前后的直方图可以看出,加密后直方图分布非常均匀,掩盖了加密前的分布规律,从而可以有效地抵抗统计分析和已知密文攻击。
2、密钥空间分析
在加密算法中使用到的密钥参数包括w0,xo,yo,μ1,μ2,γ,C,其中C取值0~255之间,其余6个参数均为实数,简单的取8位有效数字,密钥空间为256×(108)6= 256×1048。这还只是一轮加密,由此可见,用穷举攻击来解密图像文件根本不可能。
3、雪崩效应分析
常见的雪崩效应分析有密文对密钥的敏感性测试,密文对明文的敏感性测试,这里只列举前者。从图3看出即使一个参数发生微小变化,就导致密图绝大部分发生改变,从而可以抵抗差分攻击。

四、相关性测试
加密效果之一是尽可能地降低相邻像素的相关性.用如下离散化公式计算相关系数:
![]()
其中:
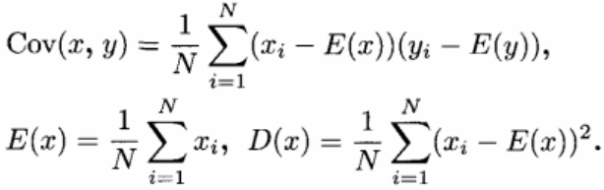
原图文件加密前水平方向和垂直方向的相关系数分别为0.872 9,0.9338,而利用本文的加密算法加密后得到的相关系数分别为0.0062,0.0059。如果单独置乱扩散加密后得到的相关系数分别为0.0172,0.0096,比较发现,置乱扩散同步的方法平均相关系数更小,对相关性的破坏程度更强。
以像素大小1000×1000的图像文件为例,将置乱扩散同步加密图像文件的加密算法的加密速度与经典算法的加密速度进行比较,加密类型为Simple-DES,Triple-DES和AES的加密速度分别为5.42s,5.76s和0.44s,而本文图像加密算法的加密速度为0.37 s,远优于其他加密算法。
小知识之雪崩效应
雪崩效应就是一种不稳定的平衡状态也是加密算法的一种特征,它指明文或密钥的少量变化会引起密文的很大变化,就像雪崩前,山上看上去很平静,但是只要有一点问题,就会造成一片大崩溃。 可以用在很多场合对于Hash码,雪崩效应是指少量消息位的变化会引起信息摘要的许多位变化。











