根据双边对角线拉伸的思想,我们提出一种利用图像加密的可逆二维混沌映射。该映射由左映射和右映射2个子映射组成,该方法通过对图像的拉伸和折叠处理,来实现图像文件的混沌加密。
一、二维混沌映射原理和算法
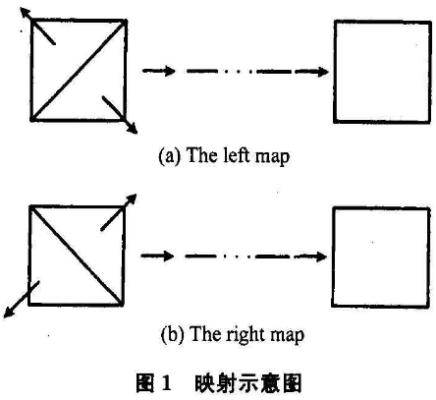
二维混沌映射利用了图像的一个重要性质:像素能够插入到其他像素间。设图像大小为N×N,通过映射首先将原图像拉伸为长N2的直线,然后再折叠成N×N的图像,如图1所示。
1、左映射算法
设A(i,j),i,j=0,1,2,…,N-1,为图像中任意一点;l(i),i=0,1,...,N2-1,t为将A(i,j)拉伸后的一维向量。如图1(a)所示,左映射算法为:
当i+j<N、i>j时,有:
![]()
当i+j<N、i≤j时,有:
![]()
当i+j≥N、i<j时,有:
![]()
当i+j≥N、i≥j时,有:
![]()
2、右映射算法
右映射算法既可以直接推导得到,也可以通过下列过程得到:
1)将原图像作一次镜像。设A,表示镜像后的图像,有:
![]()
式中i=0,1,2,…,N一1;j=0,1,2,...,N-1。
2)使用算法(1)~(4),得到右映射算法。
3、折叠算法
![]()
式中,i=0,1,2,…,N一1;j=0,1,2,:…,N-1。
二、图像文件加密、解密算法
由于映射可分为左映射和右映射。将左映射和右映射的映射次数设计为密钥Key。如Key=1234,表示图像依次左映射1次,右映射2次,然后用左映射3次,最后用右映射4次。为了保证加密效果,每一个部分密钥值都小于10。加密算法如图2所示,其中Ki及K2分别是密钥Key的一部分,可以相同或可互相推导得到,函数F(K)为密钥的函数,输出为扩散函数的参数。
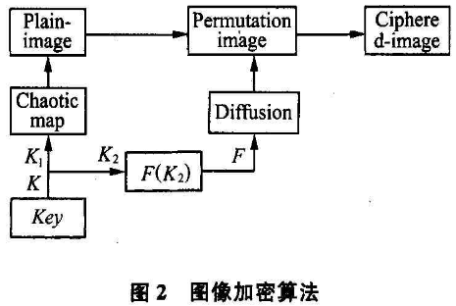
图像文件加密算法所采用的扩散函数为:
![]()
式中:νk是指每一个像素的值;v'k为扩散后的像素值;v-1=F(K2),G(v'k一1)=5×v'k一1;256灰度图,L=256。
图像加密算法分为3步:
1)利用密钥Ki及算法(1)~(5),将图像A(i,j)拉伸成一条直线l(i),i=0,1,...,N2 -1。
2)利用算法(6),将直线折叠得到置乱图像B(i,j)。
3)利用密钥K2及扩散函数,对置乱函数进行处理得到密图。
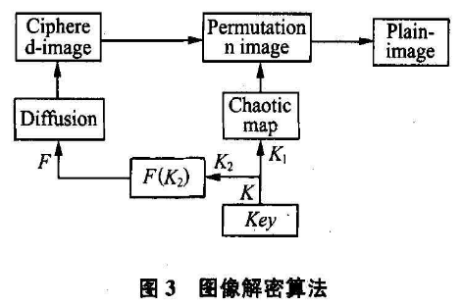
图像解密算法与加密算法相反,如图3所示。解密密钥与加密密钥相同,因此该加密算法为对称加密算法。
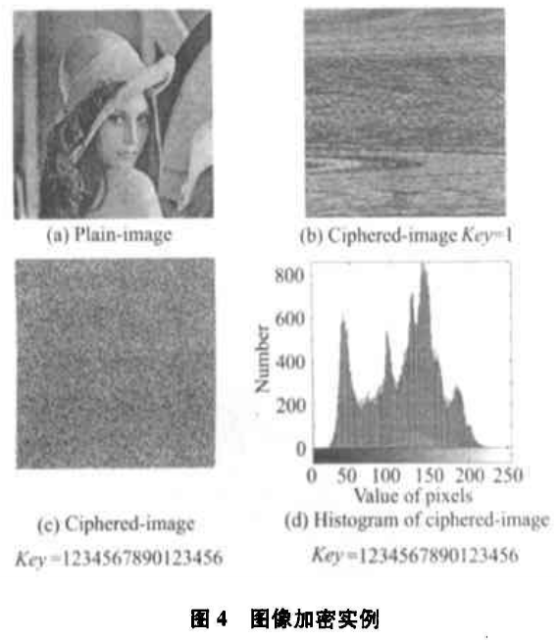
三、加密实例和安全性能分析
如图4所示,对Lena 256灰度网进行加密。为了研究二维混沌映射的加密效果,首先令K2 =0,即不使用扩散函数。此时,加密系数仅仅置乱图像,没有改变图像的像素值(直方图不
变)。当Key=1时,图像已没有原图特征;当Key=1234567890123456时,密图像素平均分布,加密效果良好。
1、安全性能分析
(1)密钥空间分析
由于最基本、最流行的破解方法是对密钥进行穷尽搜索,密钥空间大是加密算法安全的前提。图像加密算法的密钥空间(无扩散函数)如表1所示。研究表明,密钥空间大小只和密钥长
度有关,在理想情况下(计算速度允许),可认为密钥能无限增加。

(2)密钥敏感度
当加密密钥Key=1234567890123456加密时,用解密密钥Keyi=1234567890123455和Key2 =1234567890123457分别解密。如图5所示,即使加密密钥和解密密钥仅1位有最小的差异,也无法解密图像,证明对密钥差异非常敏感。

(3)统计分析
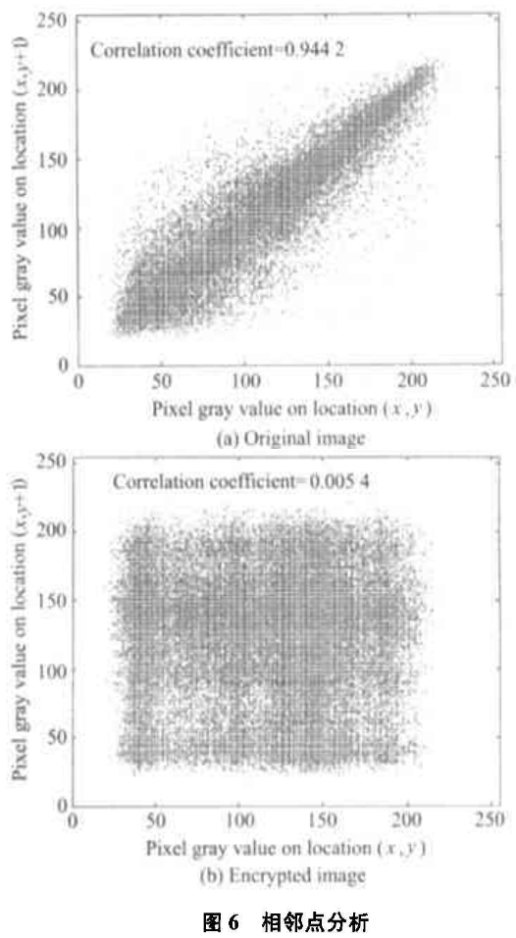
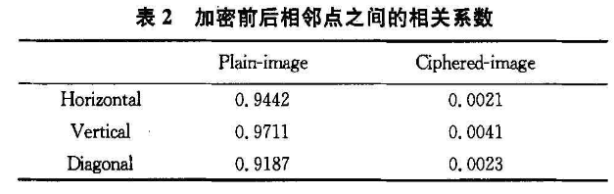
由于图像相邻像素间具有很强的相关性,如果密图相邻像素间相关性变小,说明密图安全性变强。图6为(x,y)和(x+1,y)的关系,原图的相关系数为0. 9442,加密后的相关系数为0. 0054,证明密图相邻像素间相关度接近于零。其他相邻点的相关系数如表2所示,说明密图相邻像素间相关性很小。
2、扩散算法
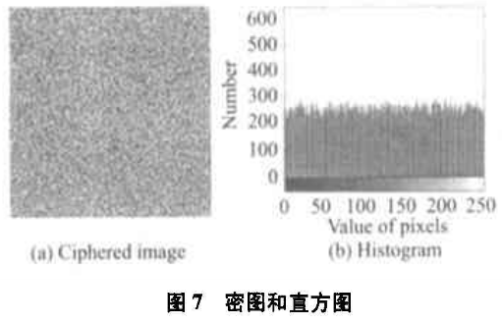
因为仅对图像进行置乱是不安全的,很难抵御明文攻击。为了增强加密算法的安全性,增加扩散函数,见式(7),其中v-1 =F(K2) =150。加密后,密图和直方图分别如图7所示。
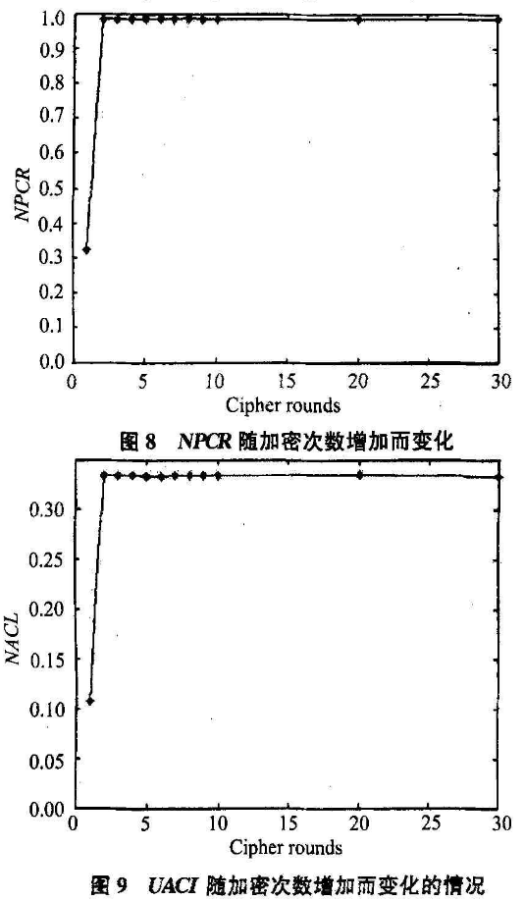
在增加了扩散机制后,对原图像只有1个像素点有差异的2个密图进行NPCR(number 0f pixels change rate)和UACl(unified average changing intensity)分析。如图8和图9所示,当
加密次数n=2时,NPCR≈I。在参数不变的情况下,2个仅有1个像素不同的图像,随着加密次数的增加,密图变得完全不同,2个原图的差别扩散到密图的整个区域,说明扩散效果良好。
四、与其他混沌加密技术的比较
和混沌流密码比较,该加密算法具有加密速度快、可移植性强的特点,由于并非直接使用伪随机混沌流掩盖明文,而是首先采用二维混沌映射置乱像素,然后利用扩散算法改变像素值。因此,从一定程度上避免了因为动力学特性退化问题带来的安全隐患,加密前后没有信息损失、移植性高,加密方法简单,易于软件、硬件实现。
和其他混沌映射比较,具有:
1)更大的密钥空间,如Baker map最大为2N-1 (N为图像的宽),而该加密的密钥空间理论上只和密钥长度有关,只要计算速度允许,密钥长度可随之增加。
2)对密钥变化更敏感i该算法将密钥设计为整个图像拉伸、折叠的数目,因此只要密钥稍有变化,密图就会截然不同。但其他二维混沌映射基本都将图像分块的数目设计为密钥,拉伸、折叠操作都是对部分图像进行的。因此,用相似的密钥可以解密密图,降低了加密安全性。
3)加密算法更加简单、清晰,易于实现。如Baker map 一般形式下的算法具有非常复杂的形式,而该加密算法非常简单,易于实现。
4)加密速度快,能够实现实时加密。
在一台PentiumⅢ(M)1.13 GHz的笔记本电脑上仿真表明,未优化的二维混沌映射的vc程序,运行速度约为3 Mbps。能满足实时文件加密需要。该混沌映射也能应用于数字水印等领域。
小知识之动力学
动力学是理论力学的一个分支学科,它主要研究作用于物体的力与物体运动的关系。动力学的研究对象是运动速度远小于光速的宏观物体。动力学是物理学和天文学的基础,也是许多工程学科的基础。











