根据数字图像的存储特点,我们提出一种基于扩展型二维元胞自动机的图像文件加密算法,该加密算法将二维元胞自动机与图像文件加密技术结合,利用元胞自动机生成数值范围在0~255区间的二维伪随机数矩阵,截取与图像大小相等的伪随机数矩阵作为密码对图像像素进行加密,解密为图像文件加密的逆过程。
一、元胞自动机原理
元胞自动机的基本组件包括:元胞空间,元胞,元胞邻域及演化规则4个部分,可用一个四元组表示:CA={Zd,Q,N,f}。元胞散布在元胞空间所划分的网格上,每个元胞具有有限的离散状态,根据不同邻居元胞状态,元胞状态在演化规则下随着迭代时间作同步更新,从而构成动态系统的演化。
二维元胞自动机的空间分布是将元胞空间划分为r×s的方形网格矩阵,每个网格代表一个元胞。用C(i,j)表示第i行,第j列的元胞,其离散状态表示为S(i,j),其中,S(i,j)∈Q。如图1所示。
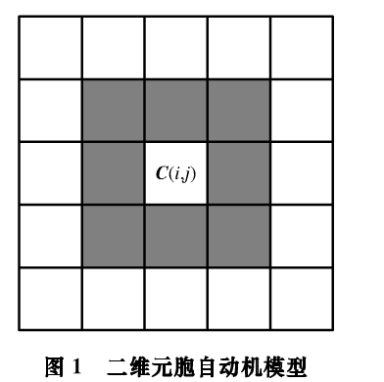
中心元胞C(i,j)包括8个邻居元胞,元胞邻域N定义为:

所有邻居元胞状态在演化规则,下共同决定中心元胞的状态,在演化规则,下的元胞状态演化式为:
![]()
即元胞C(i,j)在t+l时刻的状态由元胞邻域Ⅳ内所有元胞在f时刻的状态共同决定。由于元胞状态更新在有限的离散集合Q内,因此演化规则.厂设计原则应满足:
![]()
二、扩展型二维元胞自动机
1、扩展型二维元胞自动机模型
扩展型二维元胞自动机是种离散的动态模型,它具有自更新和自繁殖的性质。模型基本思想是在初始配置的元胞模块基础上,对元胞自动机元胞的邻居元胞进行扩展,使得模型的元胞空间随着迭代时间的增加而扩展,所有元胞状态作同步更新,即初始配置一个r×s的矩形元胞模块,根据一定的演化规则,在迭代f次后,可以获得(r+2t)×(s+2t)的元胞模块。
设在t=0时刻,初始配置一个3×3的矩形元胞模块:
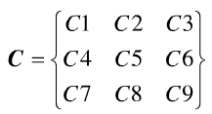
如图2(a)中的C元胞。初始配置元胞模块的元胞状态为{S1,S2,S3,S4,S5,S6,S7,S8,S9}∈Q。以C模块的任一元胞为中心元胞,根据元胞邻域定义,可得到该元胞的8个邻居元
胞,如果邻居元胞不属于元胞模块C,就标记为种子元胞M,如图2(a)中M元胞。在t=1时刻,种子元胞M根据演化规则,被扩展为元胞自动机元胞C,并获得元胞状态,同时,初始配置模块的元胞状态也在演化规则,下作同步更新。根据扩展后得到的元胞自动机元胞C的邻域定义,可得到t=1时刻的种子元胞M,如图2(b)中M元胞,在下一时刻,种子元胞被扩展为元胞自动机元胞,并产生新的种子元胞。随着迭代时间f的增加,元胞自动机空间不断扩展,元胞状态也作同步更新,实现元胞自动机的扩展和演化。
2、扩展型二维元胞自动机应用于密码学分析
在密码学中,密码设计的基本原则是扩散和混乱,本文将扩展型二维元胞自动机应用于图像加密,设计与密码设计原则有很好的对应关系的f_and扩展型二维元胞自动机模型作为研究对象。
f_and扩展型二维元胞自动机的演化规则为:
![]()
元胞模型表现出混沌复杂的性质,具有以下几个特征:
(1)元胞扩展性:元胞自动机元胞在f时刻的状态依赖于邻域内邻居元胞在t-1时刻的状态,而邻居元胞t-1时刻的状态又依赖于邻居元胞邻域内元胞在t-2时刻的状态,依次类推,元胞自动机内所有元胞状态最终依赖于初始配置C。
(2)元胞状态遍历性:任一元胞自动机元胞的状态从其生命周期开始到迭代结束,在足够大的迭代时间内,元胞状态更新局限于有限的元胞状态集,并能够遍历状态集中的所有状态。
(3)局部不稳定性:表现为局部范围内元胞的状态对初始配置和迭代时间的敏感性。对初始配置的敏感性表现为在某一时间,局部元胞的状态强烈依赖于初始配置,初始配置的微小变化会引起局部元胞状态的巨大变化。对迭代时间的敏感性表现为所有元胞的状态都会在演化规则,下随着迭代时间增加进行同步更新,局部的元胞状态在不同时间表现出不确定变化。
(4)整体稳定性:主要是指元胞自动机元胞状态整体统计特征的稳定性,它不受初始配置和迭代时间的影响,在局部不稳定的状态下保持整体统计特征的稳定性。
三、基于扩展型二维元胞自动机的图像文件加密方案
1、加密方案
本文的图像文件加密方案是利用扩展型二维元胞自动机迭代产生二维伪随机数矩阵,根据数字图像像素存储特点,将元胞自动机有限离散状态集合定义为:Q ={0~255},通过模型迭代扩展产生0~255范围内的伪随机数矩阵,并截取与数字图像大小相等的二维数据作为密码,从而与数字图像像素进行运算加密。
图像文件加密具体步骤如下:
(1)设置密钥:初始配置rxs的模块C,迭代时间t和截取随机数矩阵的起始点(x,y)。
(2)扩展型二维元胞自动机迭代r次生成大小为(r+2t)×(s+2t)的二维伪随机数矩阵。
(3)以(x,y)为起始点,截取M×N大小的二维伪随机数矩阵作为密码与明文图像像素进行异或加密,获得加密密文。
图像文件解密过程为图像文件加密的逆过程,通过秘密传输通道获得的密钥,利用扩展型二维元胞自动机迭代生成相应的二维密码,与密文进行异或获得明文。
2、仿真实验
以图像大小为512×512的Lena图像为实验对象,设置密钥C=[138 1625],t=255次,截取起点为(1,1),迭代获得大小为512×512的二维随机数矩阵作为密码对图像文件加密。
如图4所示,其中,图4(a)为明文图像;图4(b)为加密后图像。本文加密算法是对图像的无损加密,解密后图像与原图像无任何差异,图4(c)为本文加密算法的解密图像。

四、加密算法安全性分析
1、密钥空间分析
好的加密算法应该有足够大的密钥空间抗击穷举法的攻击。本文算加密法密钥组合形式多样,初始配置C的矩阵大小可任意定义,在运算速率允许下,迭代次数f也有巨大的空间。
以本实验为例,初始配置为2x2的元胞模块c:![]()
其中,每个元胞状态定义范围为0~255,共有232种组合,如果初始配置:

就有28(r+s)组合。随着迭代次数f的增加,在元胞空间扩展的同时,所有元胞状态都会作同步更新,即元胞状态在不同的时间有不同的状态。理论上C和r设置范围为无限大,所以,
对于本文算法,不可能用穷举方法获得原图像信息。
2、密钥敏感性分析
加密算法对密钥的敏感性表现为密钥的微小变化,应该得到完全不同的密码,即加密密钥与解密密钥的细微不同,会导致解密过程的完全失败。图5是用错误密钥对前面实验所获得的密文进行解密的实验结果。

在图5中,正确密钥为![]() ,t=255次,截取起点(1,1)。图5(a)是在迭代次数≠和截取起始点(x,y)相同的情况下,用错误的解密密钥对密文进行解密所获得
,t=255次,截取起点(1,1)。图5(a)是在迭代次数≠和截取起始点(x,y)相同的情况下,用错误的解密密钥对密文进行解密所获得![]()
的解密图。可以看出,在密钥有2-32的微小变化时,解密过程完全失败。图5(b)是在初始配置C和截取起始点(x,y)相同的情况下,用错误的解密密钥(迭代次数t=256次)对密文进行
解密所获得的解密图,在最小的迭代时间变化情况下,解密完全失败。由实验可知,在初始值C和f的微小变化下,获得的解密图与原图完全不同,证明了本文加密算法具有较好的密钥敏感性。
3、统计分析
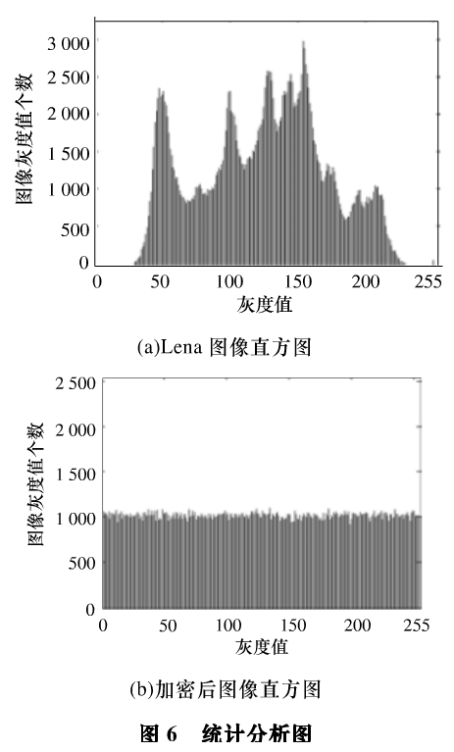
图像的直方图是图像的重要统计特征,它是图像灰度密度函数的近似。好的加密方案应该使加密后的密文图像文件像素统计特征与明文图像文件的像素统计特征有较少的联系以抵抗统计分析攻击。以本实验为例,图6(a)为Lena图像的直方图,图6(b)为本方法加密后的密文直方图,可以看到,本文加密算法获得的密文图像的直方图非常均匀,与原图联系非常小,几乎不能从密文中获得原图像的统计信息。
小知识之元胞自动机
元胞自动机(Cellular Automaton,复数为Cellular Automata,简称CA,也有人译为细胞自动机、点格自动机、分子自动机或单元自动机)。是一时间和空间都离散的动力系统。散布在规则格网 (Lattice Grid)中的每一元胞(Cell)取有限的离散状态,遵循同样的作用规则,依据确定的局部规则作同步更新。大量元胞通过简单的相互作用而构成动态系统的演化。











