基于统一混沌系统的图像加密新算法,首先,利用统一混沌系统的二维序列排序后的位置编号置乱图像像素位置。然后引进三个辅助密钥,将统一混沌系统输出的三维混沌序列两两异或后得到的混沌密钥序列对置乱图像进行逐像素加密。
一、统一混沌系统
2002年,LV Jin-hu等提出了一个新的三维混沌系统,该系统将Lorenz系统和Chen系统连接起来,而Liu系统仅为其一个特例,故称其为统一混沌系统,其数学模型为:
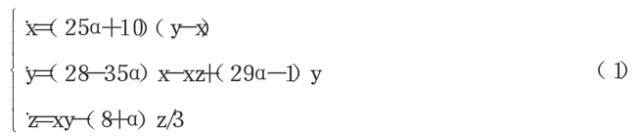
式中:系统参数a∈[0,1]在此范围内统一系统具有全域性混沌特性。当a∈匦Q 8时,系统属于广义Lorenz系统;当a=8时,系统属于广义LiLl系统;当a∈[0.8, 1]时,系统属于广义
CheIis系统。
二、基于统一混沌系统的图像加密新算法设计
1、图像像素位置置乱加密算法设计
本文的图像置乱算法中,采用统一混沌系统的前两个序列x、y来实现图像像素位置的置乱,该置乱加密算法主要是基于无周期混沌序列的排序思想。根据严格的数学证明,实数域的混沌序列是无周期的:但数字化的混沌序列由于计算机有限精度的限制将退化为周期序列。不过,在现有计算机精度下,这种数字化混沌序列的周期仍然是相当大的。因此,在一个不太长的序列范围内,通常不会出现重复的序列值。因此对于M×N的数字图像,M、N一般不会很大,如果取一个长度也等于M或N的混沌序列,则该序列中就不会存在重复值。因此可以由混沌序列的M或N个不同值通过按大小进行排序,得到M或N个不同的位置编号。
置乱算法的方法如下:
步骤1利用式(1)的统一混沌系统,间隔d取点生成长度为M的实值离散混沌序列{x1,x2,…,xm}将{x1,x2,…,xm}由小到大排序生成新的序列{x1',x2',…,xm'},因为在一定长度的范围内,混沌序列值不重复,故将实值序列{x1,x2,…,xm}中M个值不会重复,排序后每一个Xi都会有唯一的一个位置编号,确定混沌实值序列{x1,x2,…,xm}中的每一个X在排序后的有序序列中的位置编号ai形成一个新的序列{x1,x2,…,xm},其中ai为集合{1,2,...,M}中的一个值;
步骤2用步骤1同样的方法生序列y的位置编号序列{b1,b2,...,bN}其中bi为集合{1,2,...,N}中的一个值;
步骤3将原始图像像素点(x,y)置乱到点(ax,by);
步骤4重复步骤3直到原始图像中的每一个点都被置乱。完成置乱设计。
对图像完成置乱设计后,破坏了原图像的相邻想像点的相关性,但是像素点的灰度值并没有改变,即图像直方图并没有发生变化,图像的加密效果不太理想。因此需要对置乱后的图像的像素灰度值进行改变,以提高图像的加密效果。
2、图像像素值的替代加密算法设计
使用统一混沌系统产生的混沌序列对图像进行逐点加密。
对每个像素点,构造一个混沌实数序列值的密钥。这种基于统一混沌系统的像素替代分以下几个步骤进行:
步骤1在图像1中随机选择12个像素点,将其以两个为一组进按比特位异或操作,得到3个32位数字k1,k2,k3作为辅助密钥;
步骤2选择精度为32位的初值x0'、y0'、z0',与辅助密钥k1,k2,k3分别进行异或操作得到x0=x0'+k1,y0=y0'+k2,z0=z0'+k3作为式(1)统一混沌系统的初始值,参数取σ=1o,r=28,b=8/3,积分步长取0.001采用四阶Runge-Ku tta方法解微分方程,生成长度都为L(L=M×N, M×N为图像的大小)混沌序列x,y,z。
步骤3将混沌序列x中每一个实值选择小数点后第x、y、z三位组成正整数,再将该正整数对256取模运算得到1byt3的无符号整数序列x';
步骤4采用步骤3相同的方法,由混沌序列y生成1byte的无符号整数序列y;由混沌序列z生成l byt3的无符号整数序列Z';
步骤5若加密图像为灰度图像,只要对该点的灰度值进行加密,则选择Z序列作为密钥序列对进行置乱后的图像进行逐像素点加密:若加密图像为RGB真彩色图像,则要对像素点的R、 G、B三个分量分别加密,用文密钥序列对进行置乱后的图像的R分量进行加密,用y密钥序列对进行置乱后的图像的G分量进行加密,用Z密钥序列对进行置乱后的图像的B分量进行加密。完成像素值替代设计。
本加密算法不仅适合对8位灰度图像文件加密,也适合对真彩色图像文件加密。
从替代变换算法来看,由于对图像的每一个像素点都采用了不同的替代加密密钥,因此符合香农提出的一次一密加密原则。故算法具有抵抗强力攻击的安全性。
图像解密是加密的逆过程,只要利用相同的混沌系统生成相同的密钥序列,先对密文图像的像素值反替代;然后再对反替代后图像的像素进行位置反置乱,即可得到解密图像。
三、实验结果及分析
(1)加密效果

从图像文件加密效果可以看出加密图像已经变得杂乱无章,不可辨认,正确密钥能完全正确解密。
(2)统计特性分析
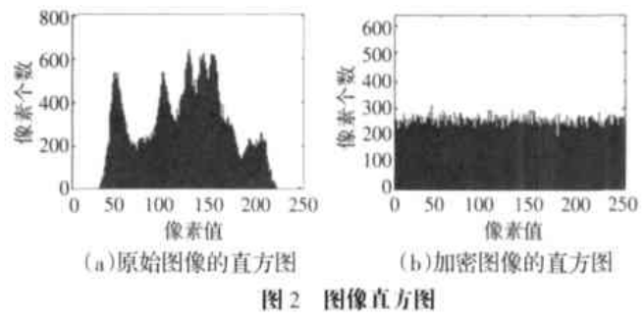
由直方图可知,加密前直方图起伏很大、分布不均匀,加密后直方图平坦、密文的灰度值呈均匀分布。这表明密文的像素值在B 255~围内取值概率均等,即对整个密文空间呈均匀分布特性:且密文的统计特征完全不同与明文的统计特征,明文的统计特性被扩散到了密文的均匀分布中,大大降低了明密文的相关性。
(3)密钥敏感性分析

将解密时所用的混沌系统初始值分别取为:x'(0)=x(0)+10-12,y'(0)=y(0),z'(0)=z(0);仅x'(0)与加密时采用的值x0相差10-12,得到解密结果如图3(b)所示。而解密时系统初值相同,仅将系统参数a与加密时采用的值相差10-12,得到解密结果如图3(协所示。可见,密钥的细微差别导致完全不能解密。对y0和z0的敏感性实验结果同样表明,当y0和z0分别改变10-12时,也完全不能解密。以上结果表明算法对密钥具有高度的敏感性。
(4)相邻像素点的相关性分析
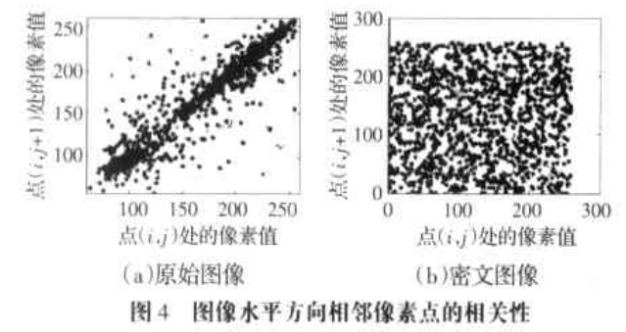
图4描述了水平方向明文和密文相邻像素的相关性。由结果可知,原始明文图像的相邻像素是高度相关的,相关系数接近于1,而加密图像的相邻像素相关系数接近于0,相邻像素己基本不相关,说明明文的统计特征已被扩散到随机的密文中。
四、统一混沌系统图像加密算法优点
(1)像素的位置置换和像素值的替代均基于复杂非线性高维混沌系统,克服了低维混沌系统不能抵御相空间重构攻击的缺点。
(2)以三维统一混沌系统的系统参数和初值为密钥,及引入了辅助密钥,大大拓展了密钥空间,使算法具有抵御穷举攻击的能力。
(3)统一混沌系统具有复杂的非线性混沌行为,因此生成的密钥具有较高的复杂性;且每次随机产生的密钥不同,具有一次一密特性,导致密文具有在整个取值空间均匀分布的特性,相邻像素具有近似于零的相关性。
小知识之置乱
所谓“置乱”,就是将图像的信息次序打乱,将a像素移动到b像素的位置上,b像素移动到c像素的位置上……使其变换成杂乱无章难以辨认的图像。











