离散分数随机变换和线性同余理论,我们提出一种单通道双彩色图像加密算法。该加密算法将输入的两幅RGB图像转换成相应的索引图像格式,其中一幅2维索引图像被编码为振幅部分,另一幅则被编码为空域相位掩模。分数域相位掩模由线性同余发生器(LCG)生成,并将彩色映射矩阵嵌入其中。引入光学幅相调制技术,在不增加光学元件的基础上来实现了双彩色图像文件加密。
一、基于DFrRT的单通道双彩色图像加密算法
1、采用LCG(Linear Congruential Generator)随机化分数傅里叶变换的核矩阵
2维信号B的离散分数随机变换表示为:
![]()
式中T表示矩阵的转置运算,p是DFrRT的分数阶。变换核矩阵Hp表示为:
![]()
其中y为本征向量矩阵,Dp为DFrRT本征值的对角矩阵:
![]()
式中t是DFrRT的周期。随机化本征向量就使Hp具有了随机性,因而生成随机化的本征向量是DFrRT的核心。目前利用计算机生成均匀随机数的常用方法是LCG法,递推关系为:
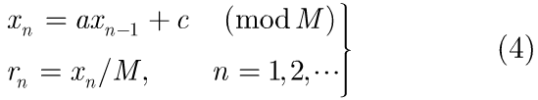
其中初值x0(0≤x0<M),乘数a(0≤a<M),增量c(0≤c<M),模数M(M>0)为算法的4个参数。利用LCG生成的随机序列重构一个2维伪随机矩阵R,并生成一个实数对称矩阵S:
![]()
矩阵S与Hp满足HpS=SHp,它们具有相同的本征向量,数值计算方法可以得到矩阵S的归一化本征向量。矩阵S是对称的随机矩阵,所以Hp的本征向量相互正交且具有随机性,LCG参数的变化将导致DFrRT结果的改变。
2、单通道双彩色图像加密算法
RGB图像可看作由红、绿、蓝分量形成的堆,索引图像是一种把像素值直接作为彩色映射矩阵下标的图像。索引图像包含两个分量:整数的数据矩阵和一个取值范围在[0,1]之间的彩色映射矩阵Z,Z的每一行都定义单色的红、绿、蓝3个分量。索引图像将每个像素的颜色由对应的整数矩阵的值作为指向Z的一个指针决定。本文加密算法将两幅RGB格式的彩图1和彩图2分别转换成索引格式图像,对应的数据矩阵为A1和A2,对应的彩色映射矩阵为Z1和Z2,把Z1和Z2嵌入由LCG生成的伪随机矩阵R中作为相位信息A3。由于R和Z的取值范围都在[0,1]之间,A3既保持了R的随机性和均匀性,又隐藏了Z1和Z2。分别对A1,A2和A3做归一化处理以限定它们在相位分布函数和振幅函数的范围中。
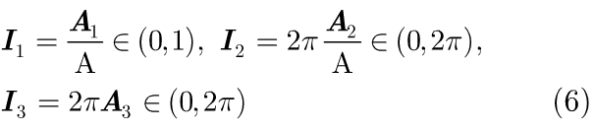
这里取A=1+max(A1,A2)。加密过程如图1(a)所示。
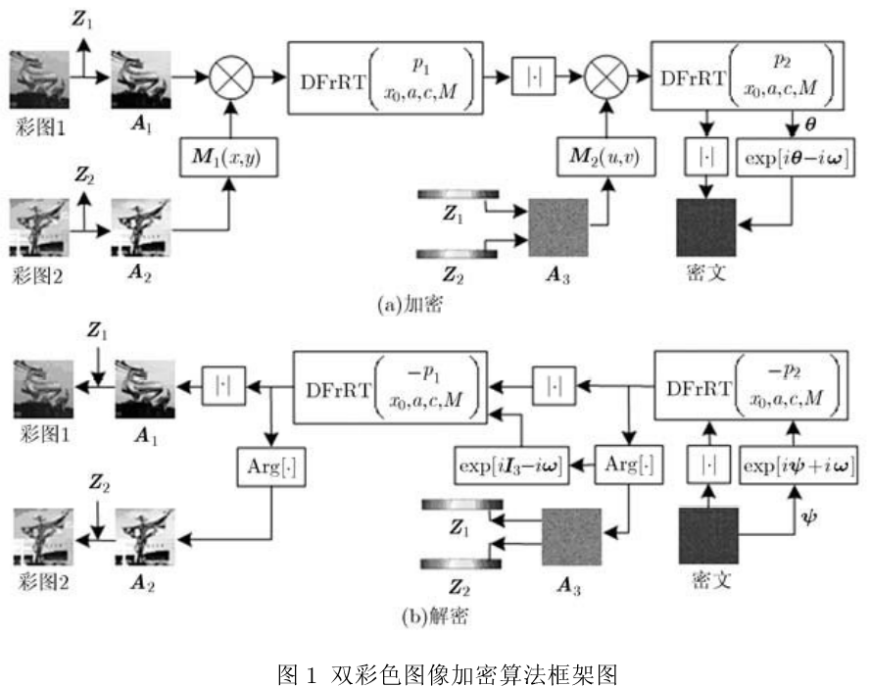
运用空间光调制器(SLM),分别将I2和I3调制成空域相位掩模M1(x,y)和分数域相位掩模M2(u,v),即:
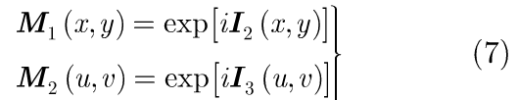
明文I1在空域被Mi调制,构成入射波函数G(x,y)= I1(x,y)M1(x,y),对G(x,y)进行一次p1阶的DFrRT,在分数域平面(u,v)上得到:
![]()
用分数域相位掩模M2对|G1|进行相位调制,|*|表示计算复函数的模值。对调制后信息进行p2阶DFrRT,在输出平面上得到的密文为:
![]()
除了传统的分数阶参数p1,p2作为密钥外,本文加密算法还增加了随机化变换核矩阵时LCG的4个参数作为密钥。相位密钥是本文算法的关键,相位密钥ω和输出相位ψ的关系为:
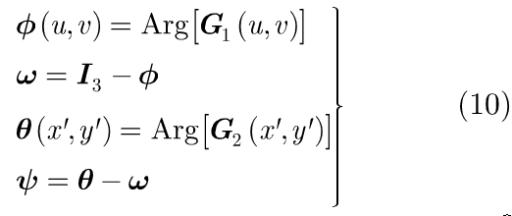
其中Arg*]表示计算复函数相位值。输出密文为复振幅函数|G2’ (x',y')|exp [iψ(x',y')]。
图1(b)所示为解密流程,是上述加密过程的逆过程。由密文相角ψ,密钥ω和|G2 |还原复函数G2 (x',y')并进行-p2阶的DFrRT,得到:
![]()
由式中相位值能恢复明文I3,通过I3减去ω计算相角φ,结合|G 1|可以在分数域平面上恢复出G1(u,v)。将G1(u,v)进行-p1阶DFrRT,I1和I2的解密过程为:
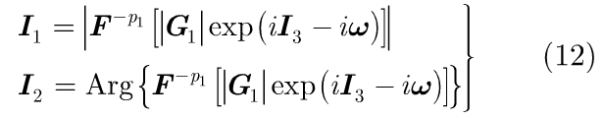
3、加密算法的光学实现
DFrRT的实现目前还没有严格的光学结构,我们需要采用一种模拟光学装置来实现DFrRT。实现单通道双彩色图像加密算法的光电混合装置如图2所示。
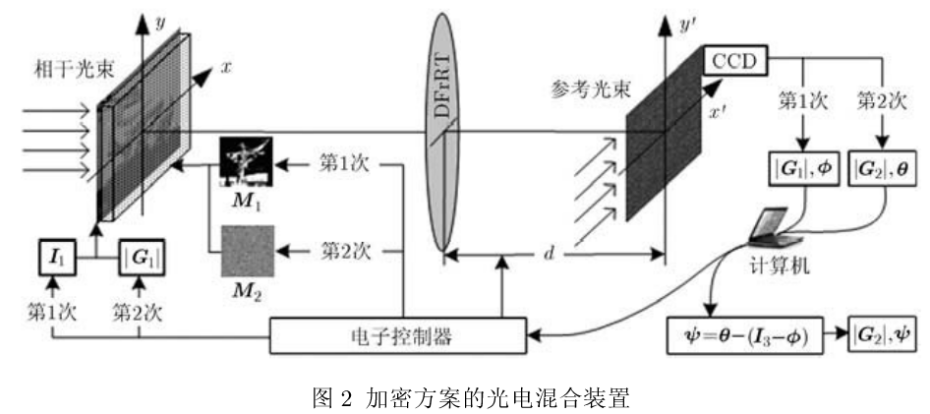
第1次光学加密实现式(8),复函数G1(u,v)的幅值可用CCD记录,相位可采用3步相移数字全息技术检测。在第2次光学加密前,SLM调制为M2,I1更换为|G1|,调整分数域距离d以实现分数阶次的改变。实现式(9)的加密过程后,再用砂对|G2|进行相位编码。因本文采用的幅相调制技术同时完成双彩色图像单通道加密,便于用光学设备实现加密。
三、双图像加密算法的数值模拟
模拟中分数阶次p1 =0.3,p2=0.6;线性同余函数的参数x0=100,a=16805,c=7,M=231-1。
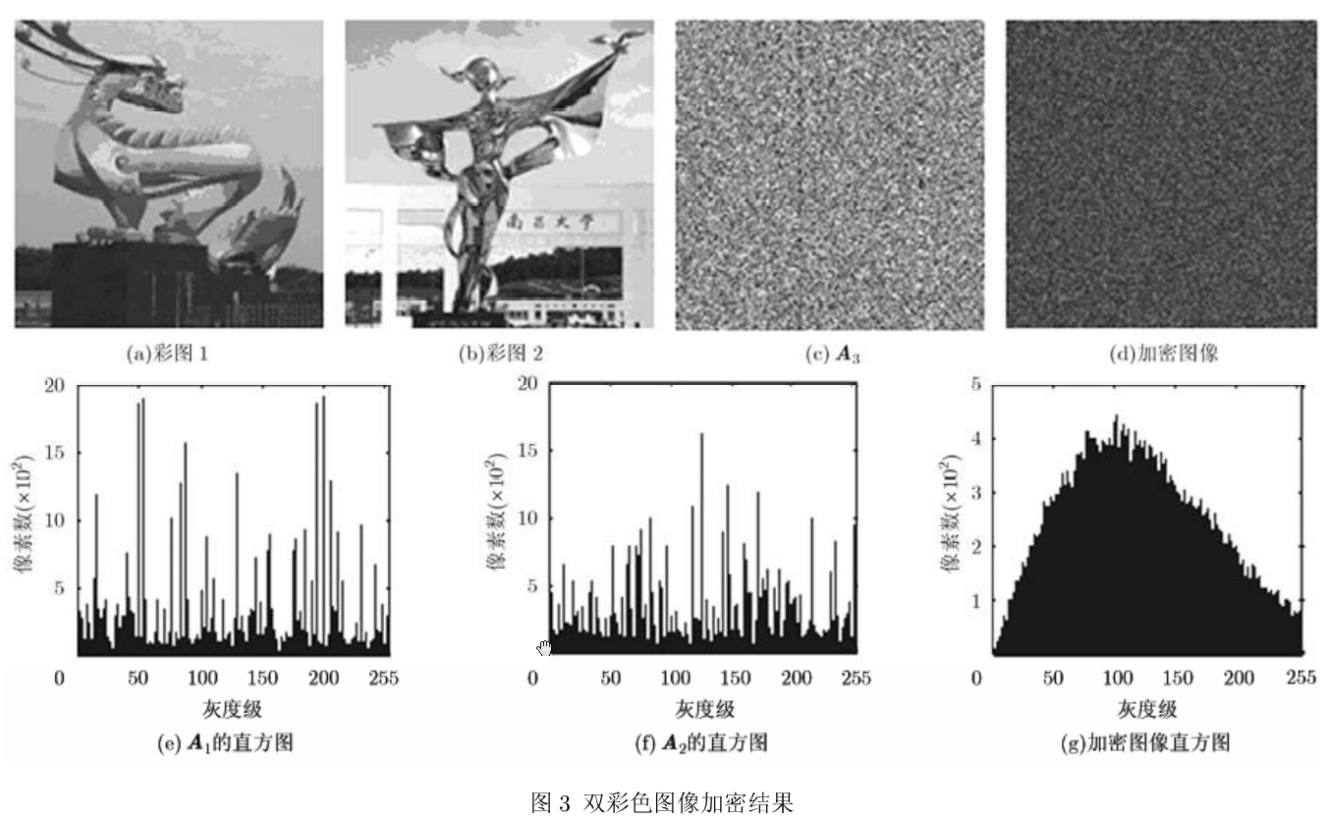
待加密的两幅原始彩色图像如图3(a),3(b)所示,图3(c)是嵌入了彩色映射矩阵Z1和Z2的伪随机相位矩阵A3,图3(d)是最终密文的振幅输出IG21,可以看出加密图像类似于噪音图像。图3(e),3(f)分别对应2维索引图像A1和A2的直方图,图3(g)对应密文振幅的直方图,加密图像的直方图明显变平滑了,密码分析者难以通过统计特性获得原始图像的特征。在密钥相同的条件下,用归一化的3幅灰度图像替代I1,I2和I3,图4表明用此加密算法加密统计特性完全不同的图像,密文的直方图非常相似。证明加密算法符合经典密码理论中的混淆与扩散思想,可有效抵抗统计分析破译。

根据彩色映射矩阵的嵌入方式,解密者可从I3还原Z1和Z2,结合I和I2还原的A1和A2恢复两幅彩色图像。当所有密钥都正确时,解密的彩色图像如图5(a)和图6(a)所示,两幅图像间不存在相互串扰。本文加密算法对不同Z矩阵同时加密,尤其适用于有高保密要求的彩色图像保护。

数值模拟中假设其它密钥均正确,仅分数阶P1偏差0.01时的两幅解密图像如图5(b)和图6(b)所示;仅分数阶p2偏差0.01时的解密图像如图5(c)和图6(c)所示;验证了分数阶密钥的安全性。为了说明LCG参数密钥的安全性,引入偏差值△,假设其它密钥均正确,图5(d),5(e),5(f)和5(g)表示LCG的4个参数分别偏差△=1时对应于彩图1的解密图像;图6(d),6(e),6(f)和6(g)表示LCG的4个参数分别偏差△=1时对应于彩图2的解密图像。

三、加密算法安全性分析
衡量解密图像和原始图像的相似程度一般采用均方误差(MSE)。h1(i,j)和h2(i,j)分别代表原图和解密图像的灰度值,均方误差定义如下:
![]()
其中M×N为图像的大小。本文设定均方误差3000作为阈值,当均方误差低于此阈值时,图像的全部信息可以被复原。
1、相位密钥安全性分析
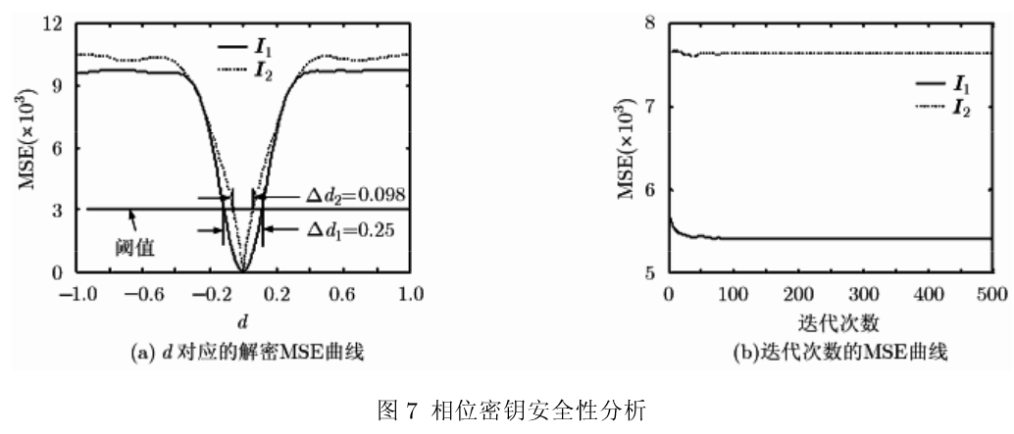
模拟中假设其它密钥正确,为了验证相位密钥ω的安全性,给ω加入一定范围的偏差,偏差后的相位密钥为ω=ω+d△r,其中d是偏离的幅度,△r是均匀分布于区间[o,27r]的随机相位。图5(h)和图6(h)所示为d-l时对应的两幅解密图像。d在[-1,1]之间变化时,对应I1和I2解密的两条MSE曲线如图7(a)所示,图中用实线标明了MSE阈值。I1和I2的MSE曲线在阈值以下部分d的变化范围△di和△d2显示于图7(a)中。相位密钥的大小为(256×256),其变化区间为[01 27r],且△d2<△d1=0.25,算法的密钥空间近似为(271/0.25)256×256≈25256x256,这个庞大的数字表明盲解密者很难实施穷举攻击。
本加密算法中,密文和相位密钥ω都与输入图像的彩色映射矩阵有关,攻击者难以获得大量的资源(如明文密文对)用于选择密文攻击,已知明文攻击和选择明文攻击。唯密文攻击只需一个完整的密文,也是常用的验证加密算法安全性的方法之一。如果攻击者已知整个加密算法和除ω之外其它的密钥,且获得了密文|G2’ (x',y')|exp [iψ(x',y')],基于相位迭代算法的唯密文攻击方案设计为:
(1)以任意随机相位ψ替代相位密钥ω,完成式(11)和式(12)的解密过程;
(2)将第(1)步解密得到的I1,I2和I3代入式(8)和式(9)的加密过程,并计算新的相位密钥ψ’;
(3)用第(2)步计算的相位密钥ψ’再次替代相位密钥ω,重复(1)到(3)步的计算,直到计算完成设定的迭代次数。
图7(b)是唯密文攻击者对图像解密进行500次迭代计算后,I1和I2解密随迭代次数变化的均方误差曲线。由图可知,当迭代计算进行100次后,MSE没有收敛趋势,并且始终大于阈值3000,图像不能被恢复,表明本文加密算法可以很好地抵抗唯密文攻击。
2、DWRT密钥安全性分析
为了考查加密方法对抗盲解密的能力,图8(a),8(b)分别对应分数阶密钥pl和p2进行了灵敏性分析,仅当p1=0.3,p2=0.6,I1和I2才能完全复原;测试发现任何一个分数阶的偏差值大于0.005时,MSE>3000,得到的解密图像有相当强的噪声。分数阶密钥具有很高的灵敏度,意味着密钥空间巨大,穷举攻击很难成功。

随机化离散FrFT的核矩阵时,把LCG产生的随机矩阵和FrFT集成为一个随机的变换,加密算法密钥数量由2重增加到6重,加密更为安全。

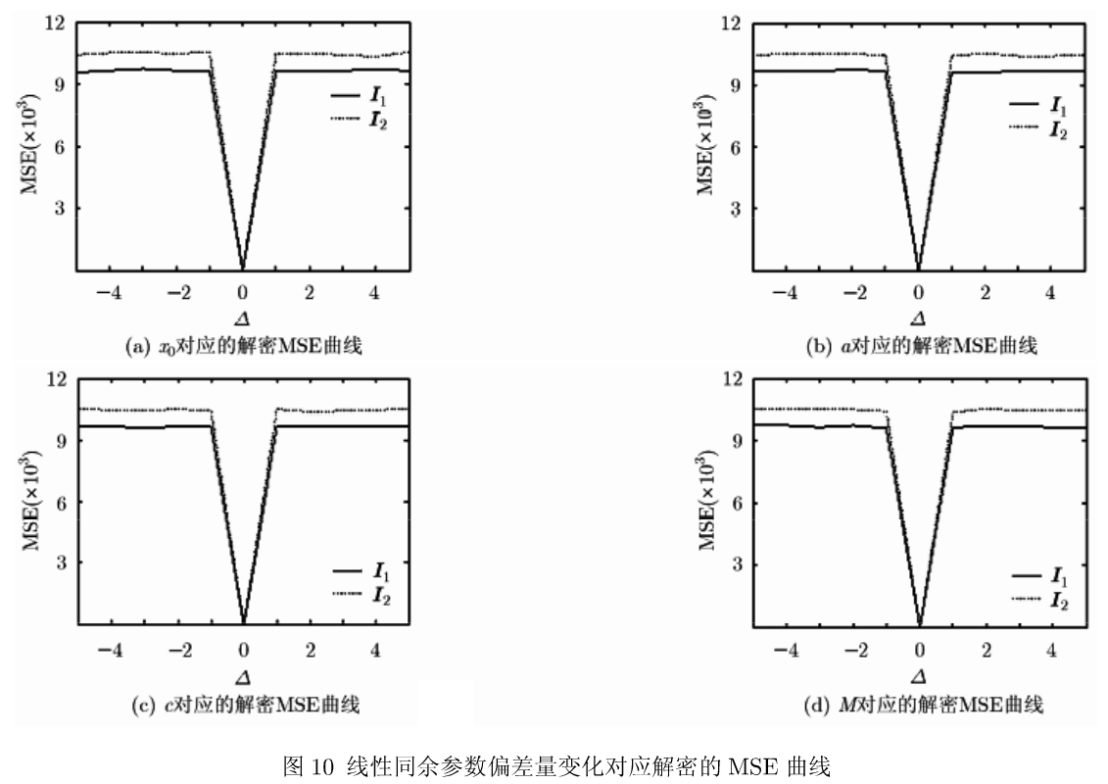
图9给出两种变换分数阶密钥对应Il解密的MSE对比,DFrRT的灵敏性明显好于FrFT。对应LCG的4个参数密钥的灵敏性分析如图10所示,任何一个LCG参数的偏差量|△|>1时,MSE>5000;线性同余函数的4个参数作为密钥具有几乎相同的灵敏性,拥有巨大的密钥空间,能有效抵抗穷举攻击。
3、鲁棒性分析
图像处理和传输过程中会有噪声的影响或物理损坏,算法抵抗噪声和裁剪攻击的鲁棒性很重要。均值为o,方差为0.1的高斯噪声Ⅳ加入|G2|,噪声干扰后加甯图像振幅为|G2 ’|。
![]()
其中k是噪声强度的系数。对应k的变化,解密图像I1和I2的均方误差变化如图11(a)所示,图11(b)和11(c)分别为加密图像受到k=0.5强度高斯噪声攻击后I1和I2的解密图像,I1的解密效果明显强于12。由图11(a)可知,随着k的增大,I2的MSE比I1的MSE增加更快,说明调制在相位部分的图像比调制在振幅部分的图像更易受噪声干扰,但两者的MSE均小于2000,表明加密算法具有良好的抗噪声攻击能力。
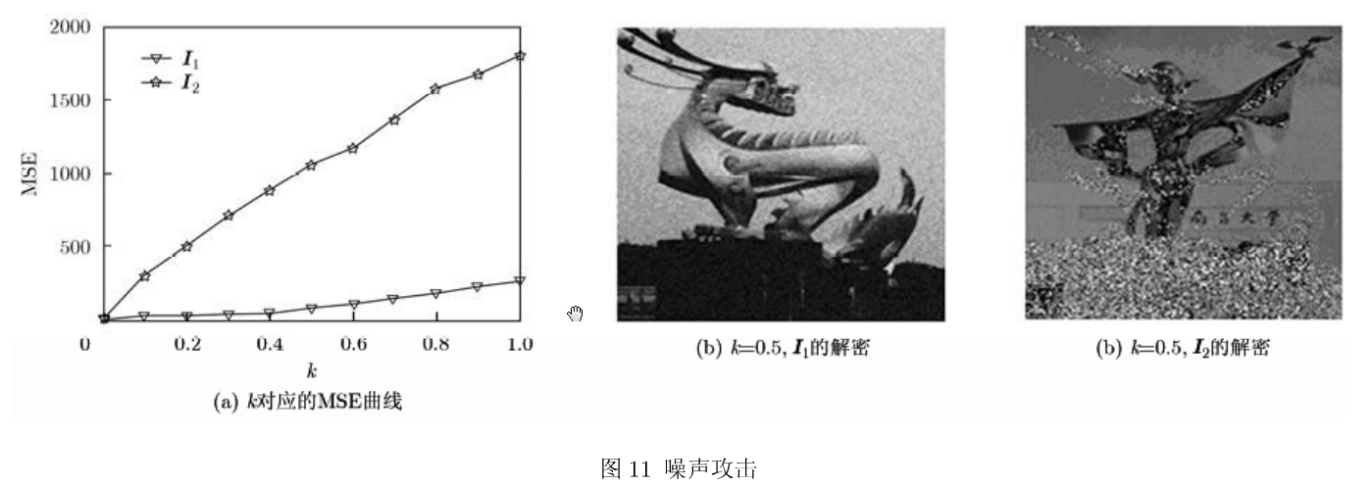
图12(a)为裁剪1/4后的加密图像,图12(b)和12(c)分别为裁剪攻击后I1和I2的解密图像。从模拟结果中可知,图像的大部分信息依旧能够恢复,该系统具有良好的抗裁剪攻击能力。

小知识分数阶
分数阶是微积分的一个分支,它对函数进行分数阶微分积分,如对函数求1/2阶导数。











