admin 扩散映射置乱与超混沌系统组合图像加密算法首先由Logistic系统构造的二维非线性动力系统产生的混沌序列形成扩散矩阵和Arnold映射矩阵，然后在基色上对彩色图像进行扩散，并在不同的位平面对彩色图像进行置乱，最后用Chen系统产生的混沌序列对置乱后的图像文件加密。该加密算法实现简单，能够抵御多种攻击，且容易用硬件实现。
一、图像置乱
在图像文件加密系统中，采用非线性函数映射置乱和线性变换进行扩散，可以有效抵御对加密系统进行的统计分析攻击。为此，扩散算法和映射算法被引进对图像进行置乱。
1、 扩散置乱
所谓扩散置乱，是指把图像中像素的灰度值用某种算法扩散到相邻的若干个像素上的图像置乱操作。对于一幅大小为N×N的彩色图像G，采用两邻点相互扩散的线性变换算法：
对图像像素的灰度值进行扩散。其中
称为2×2扩散矩阵，gij和gij+1分别为原图像点(i，j)和(i，j+1)处的三基色值，gij’和gij+1’分别为扩散后的三基色值，K为图像的
基色级，mod为模运算（下同）。为简化逆扩散运算，通常取|D|=1，且令d11=1、d12=as、d21=bs，则d22=asbs+1，称它们为扩散加权系数，取整数，由参数序列{（as，bs）}(s=1，2，…，r)决定，其中r为扩散置乱次数。那么其逆扩散为：
其中m和n为能使得0≤gij<K和0≤gij+1<K的最小整数值。如果采用三邻点扩散，则D为3×3扩散矩阵，大于三邻点扩散时D构造比较复杂，一般不用。
应用式(1)多次对图像自(0，0)开始逐行扩散，得到扩散后的图像。通常取d12≥2，这样图像中每个像素的灰度值将被放大扩散到整幅图像中，算法对被加密图像敏感a逆扩散则应用式(2)从（N-1，N-1）开始对扩散后的图像逐行反方向扩散，进行图像还原。
2、映射置乱
所谓映射置乱是把原始图像中的像素从一个位置映射到另一个位置的置乱操作。在图像文件加密置乱中的映射置乱要求可逆，如映射过程为map(x，y)：(ij)→(k，l)，即在参数x和y的作用下，把原处于(i,j)的像素移动到位置(k，l)。以达到对图像置乱的目的：为保证被置乱的图像正确还原，要求映射过程是保面积的，且映射map(x，y）必须存在相应的逆过程map'(x，y)：(ij)→(k，l)。广义Amold映射：
可以满足上述要求。为叙述方便，称
为映射矩阵。在广义Amold映射中，要求|M|=1。为简化映射矩阵构建，通常假设k11 =1、k12=d和k21=e，则J22=de+1。
到目前为止，所有采用Amold映射的置乱算法都是在图像级进行置乱。所谓图像级置乱，就是直接把图像的像素从一点映射到另一点以达到图像被置乱的目的，其置乱前后像素灰度值的统计特征没有被改变，这样在已知图像的情况下很容易受到攻击。其安全性不佳，为此，本加密算法采取基于位平面置乱。所谓基于位平面置乱，是把一幅原始图像G视作由若干个位平面组成（如256级的灰色图像有8个位平面），在每个位平面上用Amold映射对图像中各像素的比特位进行置乱操作。为了到达像素级置乱效果，在不同的位平面上采用不同的映射矩阵。其映射过程：
其中P为图像的位平面数，{ 1，dp，eP，dpep+1}为第p个位平面上所采用的映射矩阵的元素值，由参数序列{(dp，e，)}决定。由于采用不同映射矩阵，同一像素中的各个比特位将被映射到不同的位置上，从而达到像素级置乱的目的，也就是说，映射过程除了像素被置乱，同时各像素的灰度值也被置乱，原始图像的统计特征完全被破坏。
一般情况下，Arnold逆映射要计算映射周期后才能确定逆映射次数，而且该映射周期与被处理图像的大小并不成正比关系，为提高Arnold逆映射的速度和效率，有资料提出一种Arnold逆映射的新算法，但该算法不适用于广义Arnold的逆映射，且效率不高。观察式(3)不难发现，Arnold映射过程是把原图像位置(i，j)上的像素映射到（k.l）位置上，那么其
逆映射即为把(k，l)的像素映射到(i,j)位置上。因此，可以用式(3)的映射过程由(i,j)求得(k,l)后，把位置（k,l）上的像素移动到(i,j)上即实现广义Amold的逆映射过程。该逆映射方法简单，不需要进行判断，不仅可以适用于经典的Arnold映射，也适用于广义Arnold映射，无论是二维或三维均适用，而且计算时间大大缩短。
3、参数生成
在扩散置乱和映射置乱操作中，其置乱效果分别由参数序列{（as，bs）}和{ (dp，ep)}决定，为简化用户操作，同时也使得扩散和映射操作完全依赖于若干个密钥，加密算法中利用一维Logistic系统定义一个二维非线性动力系统：
来生成这些参数序列。其中为加大系统的复杂性，在二维非线性动力系统中增加了二次偶合项x2i-1，y2i-1和xi-1，yi-1。当2. 75<μ1≤3.40，2.7<μ2≤3.45，0.15<γ1≤0.21以及
0.13<γ2≤0.15时，该系统进入混沌状态，生成（0.1．0）的混沌序列。那么：
其中K的大小取决于扩散操作或映射操作。一般在扩散操作时取较小值，而在映射操作时取较大值。把生成的若干组整数类随机参数{（CxP，CyP）}作为{（as，bs）}和{(dp，eP)}参数
序列。该序列对初始值（xo，yo）十分敏感，不同的（xo，yo）将产生完全不同的随机参数序列{（as，bs）}和l（dp，eP）}，从而到达图像置乱之目的。
二、图像文件加密
1、加密混沌系统
图形图像加密算法比较多采用超混沌加密算法，常见的有Lorenz系统、Chua系统、Henon系统和Chen系统，其中Chen系统具备比其他三者更优越的动力特性，且容易用电路实现，因此，本加密算法采用Chen系统：
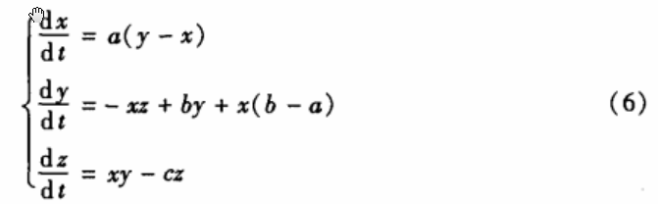
其中当a= 35，b=28，c=3时，系统进入混沌状态，其相空间具有非常优越的三维动力特性。
2、离散混沌序列
离散混沌序列产生采用如下步骤：
1）应用四阶Runge-Kutta法，取初始值为(xo，yo，zo)和分步步长为0.01对Chen系统进行数值积分，每个步长得到一组实数数值，该组数据类随机的实数型数值序列（xi；yi，zi）（i=1，2，…，M），作为初始的混沌信号序列。
2）对该混沌信号进行放大、量化和模运算：
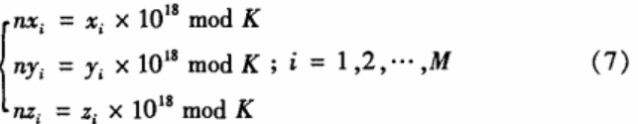
得到一组取值范围为O~（K-1）的（nxi，nyi，nzi）(i=1，2，…，m)整数混沌序列，K为图像各基色的灰度级。因为该序列是经过放大后模运算得到的，因此它对初始值(粕，Yo，zo)非
常敏感；而且由于空间非常大，使得攻击者无法从（nxi，nyi，nzi）推出（nxi+1，nyi+1，nzi+1）或（nxi-1，nyi-1，nzi-1）。
3、加密操作
为保证序列更具随机性，在整数混沌序列（nxi，nyi，nzi）中去掉迭代过程的前4000个点，取（nxi，nyi，nzi）(i=4001，4002，…，M）的整数混沌序列，组成N×N的矩阵形式(kxij，kyij，kzij)，然后用该序列与置乱后图像G'中各个像素的红、绿、兰三基色进行异或操作：
得到加密后的彩色图像G’（Credij，Cgreerij，Cblueij）(i，j=1，2，…，N)，其中0为异或运算符。由于Chen系统对初始点（X0，Y0，Z0）十分敏感，初始点有微小变化将产生不同序列。用不同的初始点（X0P，Y0P，Z0P)(P =1，2，…，m)，经过上述处理将产生完全不同的离散混沌序列（kxijp，kyijp，kzijp）(P=1，2，…，m)，用这些混沌序列对原始图像进行多次异或运算：
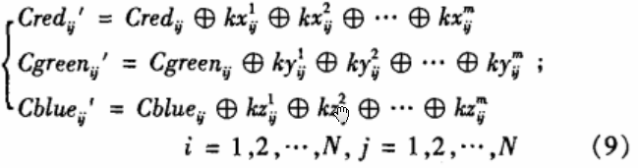
得到最终的加密后图像G'。
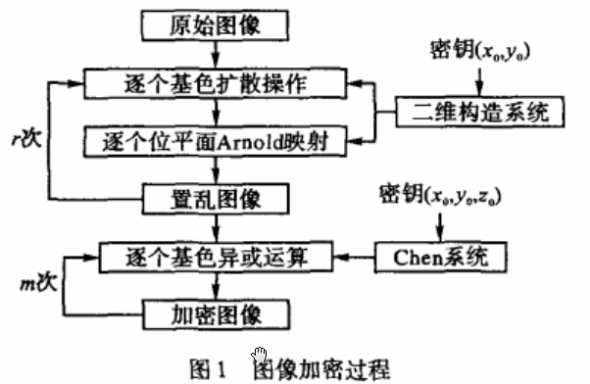
图像置乱加密过程如图1所示a整个加密过程包括置乱和加密两部分。首先在密钥(xo，yo)作用下通过二维构造系统(如式(5)所示）产生的离散混沌序列，应用式(1)对原图像的基色值进行扩散，应用式(3)在位平面上进行广义Arnold映射，扩散与映射交替进行r次，r值取决于图像要求的安全级别，一般r=3已经足够。然后在另一组密钥（xo，yo，zo）作用下通过Chen系统(如式(6)所示）和式(7)生成的混沌序列应用式(9)对置乱后的图像进行多次异或运算，以实现对图像文件加密。
三、图像文件的解密
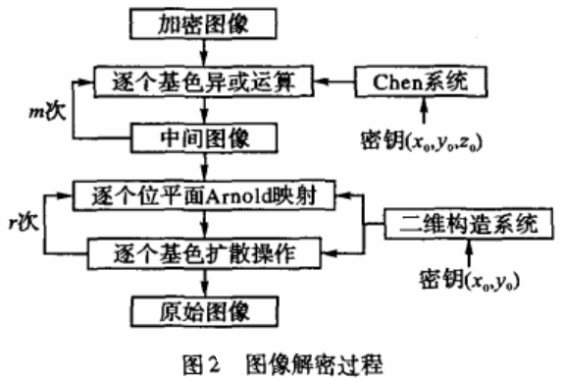
整个解密过程如图2所示。首先在密钥的作用下通过Chen系统和式(7)产生混沌序列，应用式(9)对加密后的图像进行解密。由于对图像的加密／解密采用的是异或运算，加密和解密过程完全一致，且在解密过程中只要密钥输入正确，与密钥的输入顺序无关。
接着在位平面上进行广义Amold的逆映射。如上所述，由于直接求Arnold的逆映射比较困难，在本加密算法中，直接应用式(4)通过(i,j)求得（k,l），然后把位于像素（k,l）上对应的比特位映射到(i,j)像家上对应的比特位来实现广义Amold的逆映射。在进行Amold逆映射过程中所使用的密钥序列要求和置乱时使用的序列顺序相反。
最后应用式(2)对图像的各个基色进行逆扩散操作。为了提高加密算法的安全性能，在加密过程中采用扩散和Amold映射操作交替进行，解密过程则要求Arnold逆映射和扩散交替进行。
四、实例与安全性分析
为了检验本加密算法的计算效果，在Pentium4 1.3 GHz CPU，内存为384 MB，Windows XP操作系统下，用Visual C#实现上述过程，分别对彩色水果篮和灰色的Lena图像（均为256 ×
256幅度）进行加密和解密操作，结果如图3所示。
经过扩散和位平面置乱后的图像各个像素值已经被完全破坏，加密后的图像从直观视觉效果上看几乎一样，且可以实现完全不失真解密还原，还原结果与原始图像完全一致。同时，该加密算法具有如下特点：
1、密钥空间巨大
因为Chen混沌系统和Logistlic系统对初始值（xo，yo，zo）和(x0，yo)非常敏感，只要取值得当，初始值一个非常小的变化都可以产生完全不同的混沌序列。在ViSU81 c#上，计算原始混沌序列中Chen系统的（xi，yi，zi）和Logistic系统的（xi，yi）均采用Decimal数值类型，当初始值误差为10的-18次方时，便产生不同的混沌序列。也就是说，解密密钥和加密密钥只要有10的-18次方的差别就无法进行解密。同时每组密钥有五个值(即二维构造系统中的(xo，yo)和Chen系统中的（xo，yo，zo）），它们在实数域中的取值不受任何限制，同时允许多次加密，具有非常大的密钥空间，可以抵御密钥穷举攻击。
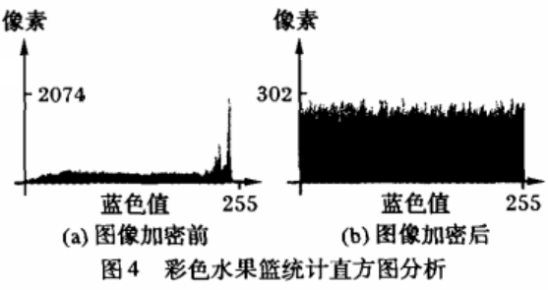
2、具有良好地抵御统计攻击能力
对图像文件加密的另一种攻击方法就是对图像进行直方图分析。图4所示为水果篮图像文件加密前后的统计直方图，图像加密后其各个颜色值均匀分布，平均基色值在(127. 42-127. 53)，像素较均匀分布在各个基色值上，最大像素个数为302个。由此可见，加密后的图像的统计分布完全被破坏，具有很好地抵御统计分析的能力。
3、能够有效抵御像素相关统计分析攻击
为了说明加密后图像的相关特征被完全破坏，随机取一些点，以该点为中心，计算其相邻各个点颜色值数学期望值、自相关和互相关以及协方差。每种颜色的自相关值为：
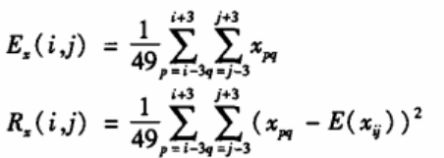
颜色之间的互相关值为：
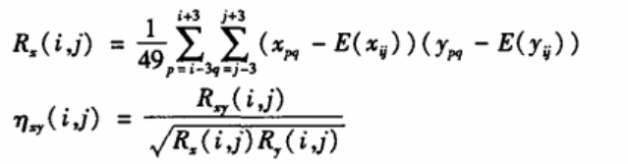
应用上述计算公式，分别取像素(i,j)为中心的7×7点阵进行分析，分析结果如图5所示。
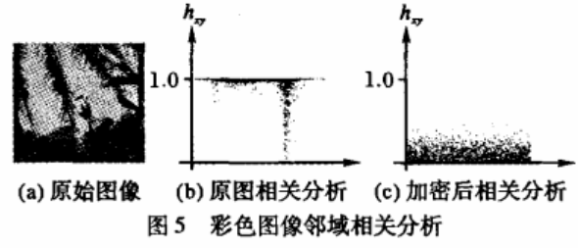
图中给出彩色图像文件加密前后随机选取的6000个像素邻域相关分析结果。可以看出，原图像的大部分像素的邻域相关性在1.0附近，而加密后的图像各个像素的颜色值相关性非常小，因此，该文件加密方法可以有效地抵御采用像素相关分析的攻击。
小知识之置乱
所谓“置乱”，就是将图像的信息次序打乱，将a像素移动到b像素的位置上，b像素移动到c像素的位置上……使其变换成杂乱无章难以辨认的图像。
