传统的加密算法往往比较复杂而难以掌握,复杂的加密算法往往大大增加程序的复杂度,同一算法加密结果不变又降低了加密结果的抗破解能力,我们经过对线性同余序列数据特征的研究以及在实践中经过长时间摸索与检测,我们在基于线性同余序列的基础上提出了一种实用的加密方法,简单、容易实现;在尽量不损失加密强度的情况下提高了加密和解密速度,同时,同一输入得到的加密结果输出不同,一定程度上增强了抗破解能力。
一、伪随机数与随机序列
真正意义上的随机数(或者随机事件)在某次产生过程中是按照实验过程中表现的分布概率随机产生的,其结果是不可预测的,是不可见的。而计算机中的随机函数是按照一定算法模拟产生,其结果是确定的,是可见的,由此可见,这个可预见的结果其出现的概率是100%,所以用计算机随机函数所产生的“随机数”并不随机,是伪随机数,伪随机数有2个特点:
1、在某一整数范围内产生足够多的随机数的时候数据在该范围内均匀分布,也就是说取到各个整数值的机会均等。
2、连续产生的随机数在较大范围内不能序列重复。
这里的序列重复是指不应该像循环小数一样存在循环节,当然,绝大多数随机数产生算法还是有循环节的,但这个循环节往往非常长。
鉴于这2个特点非常适合用作加密。任何数据经过随机序列掩码产生的结果也将具备如上的数据特征,掩码后的结果在不知道掩码序列的情况下将很难逆推回原序列,我们就以这种思路来构造加密算法。
二、大数同余
快速产生随机序列是提高本方法加密速度的关键,我们研究了一下Visual C++,Turbo C和Delphi的随机序列产生办法,它们采用的都是大数的线性同余序列。设m是一个给定的正整数,如果2个整数a、b用m除,所得的余数相同,则称a、b对模m同余。所谓线性同余法(又叫混合同余法),就是这样的一个公式:
![]()
经前人研究表明,在M=2q的条件下,参数A,C,X[O]按如下选取,周期较大,概率统计特性好。
![]()
X[O]为任意非负数。
同余序列总是进入一个循环,这是一个事实,最终必定在N个数之间无休止的重复循环。
三、新的随机数发生器
如上所述,即便采用唯一的随机序列发生器产生的随机序列进行掩码,也可以得到均匀分布的加密结果,当然这样的加密在预知加密算法的前提下对密码进行碰撞还是很容易解密的,这就需要迸一步的增强密码空间,加大碰撞难度。这里可以利用线性同余算法对于不同的因子可以产生不同的随机序列这一特点,使加密过程和密码长度关联起来,构造一个新的随机数发生器,它的因子是密码相关的。
很明显,常见密码是可视字符的组合,为了讨论方便,不妨按照常见的密码设置:英文字母,数字和下划线的组合,称为密码空间,这样密码就可以表示为函数:
![]()
符号&表示连接。
以上为因子的随机序列表示为函数RandomSequence(x),根据随机序列的定义,RandomSequence(x)为x相关的整数有序集合,RandomSequence(x)_Z且当ri≠X2时有andomSequence(x1)≠RandomSe-quence(x2)。
定义函数Select( X1,X2,X3,...,Xn,m)为X1∪_X2 ∪_X3 ∪...∪Xn到{X|X∈X1 ∪X2 ∪X2∪...∪Xn)的一个映射,其中X1~Xn为有序集合,m∈Z+,表示顺序的从X1~Xn取第1个值,取到墨后返回X1继续取X1的第2个,X2的第2个以此类推,直到取m个值为止。
对于密码Mix(x1,x2,x3,…,xn),随机序列就是Select(RandomSequence(X1),RandomSequence(X2),RandomSequence(X3),…,RandomSequence(Xn)m)。m的取值和被加密对象的长度相关,很明显,如果原随机序列周期为p,采用这个方法后实际上随机序列的周期将变为pn,同时,要碰撞出这样一个序列的话需要验证的密码要在71个密码空间的笛卡尔乘积中选取,即便在当前的设定下.1个密码空间的长度为63(大小写字母,下划线和0~9的数码),九个字符长度的密码对应的密码数量将为63n,只要长度足够(实际上4位的密码634 -15 752 961,就已经上千万了),穷举破解在时间上应该是不可能的。
四、加密与解密
在随机序列已经构造的前提下,加密解密是一个非常简单的过程,这里为了实用性我们对加密对象做了以下区分:
A.密文可视的;
B.密文可视无关的。
对于A类,是指存储在文本文件或数据库中的数据片段,这类数据往往有些格式要求,比如加密结果不能包含0或者其他的特定字符,但可用范围往往可以界定.B类就是没有这种考虑的加密对象,很明显,一个加密算法对不同的对象进行区分不太合适,还不能增加算法的复杂度;
I.以字节为加密单位进行换码加密。
Ⅱ.换码的范围由加密者指定。
这样就将A,B两类对象又整合为同一类对象了,为了适应这种情况,在Select(RandornSequence(x1),RandomSequence(x2),RandomSequence(x3),…,RandomSequence(xn)m)中取值后需要对相应范围取模,假定给定范围为[a,b],原文k1 k2k3…km,密码Mix(X1,X2,X3,…,Xn),Select( RandomSequence(x1),
RandomSequence(x2),RandomSequence (x3),…,RandomSequence(xn),优)中取的第j个值为Radj,令:
![]()
则换码加密函数为:
![]()
换码解密函数为:
![]()
加密算法类似于补码运算,应该不需要做解释,可以简单验证。
原文为'A'(Ascll码为65),范围为[32,127](ASCII可视范围),则Rddj不妨假设为100,则rj=100 mod (127-32+1) -4。
加密
(65-32+4) mod (127-32+1)+32=37 mod 96+32=69
65变成了69。
解密
(69-32+(127-32+1-4)) mod (127-32+1)+32-129 mod 96 +32-65
69变回了65。
本加密算法已经使用VC 2008实现,使用一般字符串测试,范围设定为[32,127],数组测试使用范围[0,255],结果如图1。
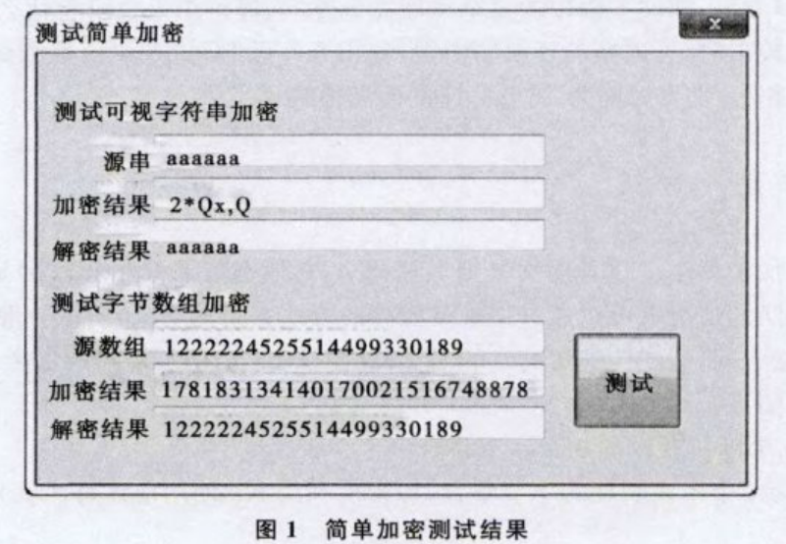
从图1可以看出,掩码后失去了原文的一切特征,即便原文为重复字符,掩码后内容也完全不同,从密文测度原文是不可能的.对这一点,笔者特别针对图片做了一个测试,采用2幅图片,一幅纯白(rgb(255,255,255)),一幅为复杂图像,测试结果如图2。


从图2和图3可以看出,即便2幅图的复杂程度完全不同,掩码结果也没有什么太大区别并且完全看不出原图效果,在未受到攻击时,可以精确还原原图像,使用GetTickCount64函数测试,没做任何优化的情况下一幅256k 24位真彩图片文件加密时间为16 ms,速度已经很快了。
五、关于不定态结果
一般情况下,对于加密算法f以及明文x及其密码p,其加密结果R=f(x,p)是唯一的,这样的话如果有密文,在已知加密算法的情况下可以通过逆推及碰撞的方法去猜测明文,所以一般的加密方法要求尽量采用长密码串以扩大碰撞空间,达到防破解的目的,笔者的想法是在原文、密码的加密基础上在密文中增加一个扰动量,其加密规则如下:
1、定义扰动量Kn为随机获取的n个字节集合。
2、原加密密码x为一个不定长度的字节集合,加密前利用Kn使用前述算法p对密文进行扰动,变换为:
X=p(x,Kn)
3、针对前述算法,使用X对原文S加密形成初步加密结果r=p(S,X)。
4、将Kn合并到r的固定位置形成最终密文R=Kn∪r。
解密时:
1、对密文R切除指定位置的n个字节得到密文r和扰码Kn。
2、使用Kn对密码z进行扰动变换(同加密)X=p(x,Kn)。
3、使用X对r进行前述加密变换的逆变换得到原文S=p-1(r,X).
过程比较简单,其优点在于扰码可以随意获取,而随扰码的不同加密结果在形式上也随之变换,从密文难以推导原文。
小知识之随机序列
随机序列(random sequence),更确切的,应该叫做,随机变量序列。随机变量序列,也就是随机变量形成的序列。有时候为了简称,省略了变量二字。











