目前,在几何造型系统中的曲线曲面大多是以基函数模型的不同来构造的。因此,在几何造型领域中的信息文件加密主要是通过对其相应的基函数的改变从而达到对其曲线曲面的加密。为此,我们提出了一种基于基函数系数矩阵混合的加密算法。通过此加密算法可以对三次均匀B样条曲线曲面基函数的系数矩阵进行混合,从而达到对曲线曲面的加密。
一、基函数系数矩阵的混合
定义1 若矩阵F和G分别表示不同的自由曲线基函数的系数矩阵,α为满足0≤α≤1的任一实数,则称矩阵S:
![]()
为系数矩阵F和G的仪混合矩阵。 根据混合矩阵的定义,当混合参数α接近1时,混合矩阵S就接近于矩阵F,当混合参数α接近0时,混合矩阵就接近于矩阵G。这样就可以利用此算法,将两类不同的自由曲线的系数矩阵进行混合,从而实现对其中一类曲线曲面的加密。加密后的系数矩阵可以用下面的公式恢复:
![]()
二、基于矩阵融合的三次均匀B样条曲线曲面的加密
B样条采用具有最小支承性质的B样条函数作为基函数,利用控制顶点定义曲线曲面,不仅继承了Bezier方法所具有的优良的控制性质,并且具有Bezier方法不能比拟的优点:局部性,修改某一控制顶点只影响到与其相关的几个控制顶点;与控制多边形的逼近程度好。由于上述优点,在当前的CAD/CAM系统中,B样条曲线曲面已经成为几何造型的核心部分圈。 由于B样条模型的广泛应用,相应的就应该考虑它的加密问题,如果不对其进行处理的话就很容易遭到复制。下面将利用上述算法将三次Bezier曲线基函数的系数矩阵与三次B样条曲线基函数的系数矩阵加以混合,从而达到对B样条曲线和曲面的加密。
1、三次Bezier曲线基函数
Be zier曲线是以Bemstein多项式作为其基函数的,也叫Bemstein基函数。如下形式的多项式称为n次Bemstein基函数:
![]()
其中:
![]()
由式(3)可得:三次Be zier曲线的基函数为:
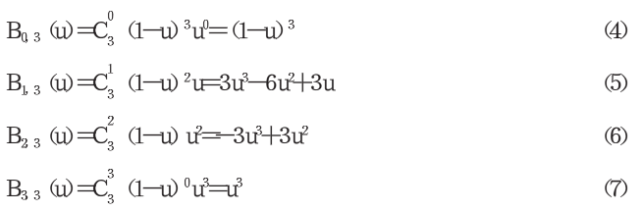
由式(4)、(5)、(6)、(7)可得三次Be zier曲线基函数的系数矩阵F为:

2、三次B样条曲线基函数
给定参数u轴上的节点分割![]() ,称由下列递推关系所确定的Bik(u)为Tn k上的k次B样条基函数:
,称由下列递推关系所确定的Bik(u)为Tn k上的k次B样条基函数:
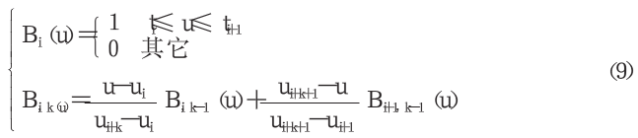
并约定0/0=0,式中k表示B样条的幂次,u为节点,下标i为B样条的序号。 由式(9)可得:三次B样条曲线的基函数为:
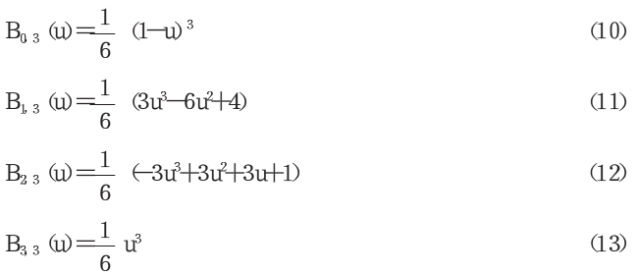
由式(10)、(11)、(12),(13)可得三次B样条曲线基函数的系 数矩阵G为:

3、α混合矩阵S
根据混合矩阵的定义,由式(1)可得:α混合矩阵S为:
![]()
将上述三次Be zier曲线基函数的系数矩阵F和三次B样条基函数的系数矩阵G带入上式并化简可得:
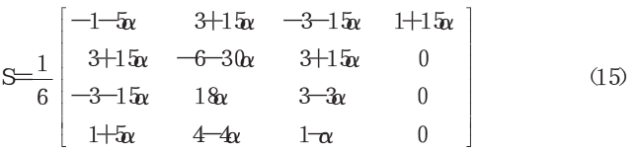
以混合矩阵S作为系数矩阵的样条的基函数为:


三、基于矩阵融合的三次B样条曲线曲面加密算法实验结果
1、三次均匀B样条曲线的加密
三次B样条曲线段的矩阵表示为(以系数矩阵G为基函数)
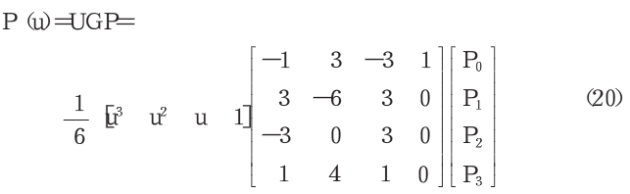
经过系数矩阵混合后(以系数矩阵S为基函数)

实验中,给定四个控制顶点Po(2,1)P1(3,4)P2(4,1)P3 (5,4),由这四个控制顶点可以确定一条B样条曲线。图1给出了没有加密的原始的三次B样条曲线;图2给出了经过与三
次Be zier曲线基函数混合后不同取值的混合参数仪所对应的加密曲线。
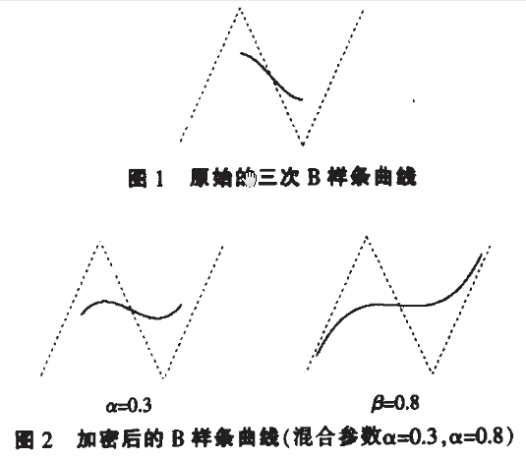
2、双三次B样条曲面的加密
本文只讨论了对双三次B样条曲面的加密。双三次B样条曲面片由包含16个顶点的特征网格定义。令网格为V:

双三次B样条曲面片的方程为:
![]()
式中:
![]()

经过系数矩阵混合后,以矩阵S作为基函数的双三次曲面片为:
![]()
式中只有基函数矩阵G替换为矩阵S:

试验中,给出16个控制顶点分别是V11=(10 ,0),V12=(9.5,2.5), V13=(10.5,4.5),V14 =(11.5,5.5),V21=(8, 2), V22=(8 ,4), V23=(9,6), V24=(10, 7.5),V31 =(6, 3),V32=(6,5), V33 =(7,7),V34=(8,8),V41=(4,2),V42=(4 ,4),V43=(6, 6),V44=(6, 7.5)。图3给出了没有加密前的双三次B样条曲面,图4给出了经过系数矩阵混合加密算法加密后混合参数α的不同取值所对应的双三次B样条曲面。

试验结果表明,利用α混合矩阵生成的曲线曲面和原始的B样条曲线曲面有一定相似度,并且可以通过调整混合参数仪的大小来得到满意的加密结果,从而能够较好地隐藏原始的B样条曲线曲面。
小知识之B样条基曲线
在数学的子学科数值分析里,B-样条是样条曲线一种特殊的表示形式。它是B-样条基曲线的线性组合。B-样条是贝兹曲线的一种一般化,可以进一步推广为非均匀有理B样条(NURBS),使得我们能给更多一般的几何体建造精确的模型。











