基于分数傅立叶变换生成序列多样性的图像加密算法

为了增强分数傅立叶变换在图像信忠加密领域的复杂性，我们提出了一种基于分数傅立叶交换生成序列多样性的图像加密算法，这种加密算法根据分数傅立叶变换的生成序列的多样性，构造不同的分数傅立叶变换的核函数，利用各级的生成序列、二维变换阶次以及相位编码时使用的随机矩阵作为算法中的密钥，对相位编码后的图像进行3次不同的分数傅立叶变换，达到对图像文件加密的目的。

一、分数傅立叶变换及其生成序列的多样性

分数傅立叶变换(fractional Fourier transfonn，HFr)是傅立叶变换的一种广义形式。

1、分散傅立叶变换的生成序列

{φn(t)；n∈N}是构成傅立叶变换(Fourier transform，FT)的特征函致的复规范正交基，满足如下条件：

FT相应的特征值μn可以表示为：

结合傅立叶级数的性质，由FT的规范正交基和特征值可以导出FT的函数的展开式：

分数傅立叶变换是通过选取和傅立叶变换算子相同的特征函数并将其特征值分数化得到的，将式（3）中的特征值μn用它的α次幂μαn代替即可得到分数傅立叶变换的核函数表达式：

傅立叶变换和分数傅立叶变换都是选取Hennite-Gauss( HG)函数作为规范正交基，如下式所示：

式中，Hn(t)=(- 1)net2dne-t2/dtn是N阶Hennite多项式。

如同开平方运算可以得到多个值一样，一个复指数的实数次幂的运算结果也是不惟一的，特征值的分数次幂μαn的所有可能值为：

式中，qn是任意整数序列，选择不同的qn将导致不同特征值，因而产生不同的分数傅立叶变换的定义，称gn= n+4qn(n=0，1，2，…)是FRFT的生成序列。因此，由于生成序列的多样性可以产生的多种分数阶傅立叶变换的核函数，导致分数傅立叶变换的定义不是惟一的，而是存在多种形式。

2、分数傅立叶变换的多样性

分数傅立叶算子Fα主要由其核函数以ψα(f,t)决定，信号s(t)的α阶分数傅立叶变换可以写成：

1）当gn=n时，由式(4)、(5)和(6)推导可以得到FRFI'的核函数：

结合式7，即得到信号s(t)的分数傅立叶变换：

式中，α是分数傅立叶变换的阶次，

2）当gn=n+8时，由式(8)和(9)可以得到信号s(t)的分数傅立叶变换为：

3）当gn= 3n时，同理可以得到信号s(t)的分数傅立叶变换为：

3、二维离散分数傅立叶变换

对于二维的图像信号I(P，Q)，其二维离散分数阶傅立叶变换和反变换分别为：

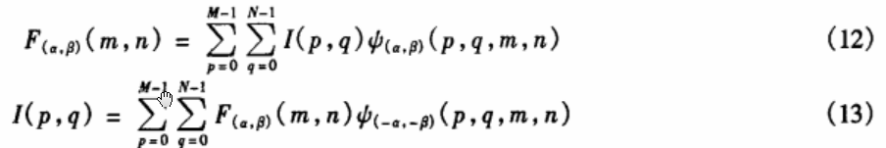
基于分数傅立叶变换生成序列多样性的图像加密算法

式中，ψ(α，β)（p，q，m，n）=ψα*ψβ，ψα和ψβ为一维离散分数傅立叶变换的核函数。

二、图像的加密和解密算法

本文提出的图像加密流程如图1所示。首先使用相位函数ej2dr与图像I(i，j)相乘进行相位编码，其中φ1，φ2，φ3均是均值为0、方差为1的随机矩阵，该矩阵和图像大小一致。相位编码后，选取g = n时的分数傅立叶变换方式进行阶次为(P1，P2)的第一级加密，产生I1(i，j)。随后分别产生随机矩阵φ2，φ3，来进行相位编码，使用（n +8）、(3n)作为生成序列gn，选取(P3，P4)和(P5，p6)作为分数傅立叶变换的阶次进行第2级和第3级加密，最后得到加密后的图像I3(i，j)。

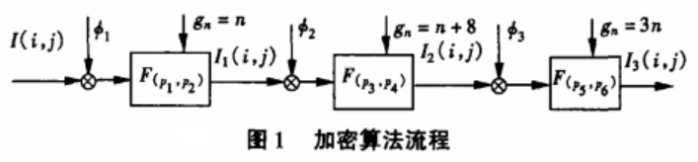
基于分数傅立叶变换生成序列多样性的图像加密算法

在对图像进行解密时，必须知道进行各级相位编码的随机矩阵φi(i=1.2，3)，各级分数傅立叶变换的生成序列gn以及每次进行二维分数傅立叶变换的阶次(pi，pj)，才能获取正确的解密图像。

三、仿真实验结果

仿真实验中，我们选取256×256的Jena灰度图像I(i，j)作为测试图像，如图2(a)所示．随机产生φi(i=1，2，3),选取3次二维分数傅立叶变换的阶次均为(0.88，1.06)。加密后的图像如图2(b)所示，在获取正确密钥时，解密后可以得到和图2(a)相同的图像。

基于分数傅立叶变换生成序列多样性的图像加密算法

实验结果表明，在解密过程中，第3级的分数傅立叶变换阶次（- P5，- p6）敏感度最强，只要它有微小的改变，即使在其他2级变换阶次（-p3，- P4），(-P1，- P2)，随机矩阵φ2，φ1和2个生成序列gn全部都正确，也无法得到正确的解密图像。当选的p5= 0.78，P6=1.06，且其他密钥均选取正确数值，解密后的图像(如图2(c)所示）和原始图像相差甚远。图2(d)显示了P1，P3，p5的偏离对解密图像带来的影响。图2(d)中的横坐标为各级变换阶次的偏离量，纵坐标是解密后图像的均方误差(MSE)，具体算法为：