图像加密就是对图像进行某种变换,使得变换后图像与原始图像存在颜色流度、或者轮廓等定性或定量等视觉差异,从而可以有效地保护图像数据,为重要图像信息的传输提供一种安全保障。我们利用拉伸和折叠的原理,提出了一种可逆映射集合的图像文件加密方法,将不同的拉伸映射和折叠映射相互组合建立一个可逆混沌映射的集合,密钥设计为集合中可逆映射的种类,来实现图像文件加密。
一、拉伸和折叠算法
拉伸和折叠算法就是通过特定的映射,将图像像素的位置置乱,并将置乱后的像素排成一个向量,再将这个向量按照一定的顺序折叠成与原图大小—致的图像,完成对图像像素位置的置乱。
1、拉伸算法设计
(1)Line map的拉伸算法设计
Line map拉伸算法包括左映射和右映射。图像的左映射分成3个部分,如图1(a)所示。第1部分是第1条虚线左上部,奇数斜行中的像素向偶数斜行里插入,形成新的向量。第2部分是两个虚线之间的部分,斜行之间的像素按顺序两两互插。第3部分是第2条虚线右下部,斜行中的像素(4,4)、(3,5)、(2,6)、(1,7)插入到像素(4,5)、(3,6)、(2,7)中;像素(4,6)、
(3,7)和像素(4,7)构成向量(4,6)、(4,7)、(3,7)。然后再将这些向量首尾相接构成一个向量,完成左映射。
图像的右映射与左映射类似,只是插入时从右上角开始至左下角结束,如图1(b)所示。

左映射算法和右映射算法类似,这里仅给出左映射算法,假设维数为ⅣXM的图像矩阵A,则当N<M时,左映射算法如下:

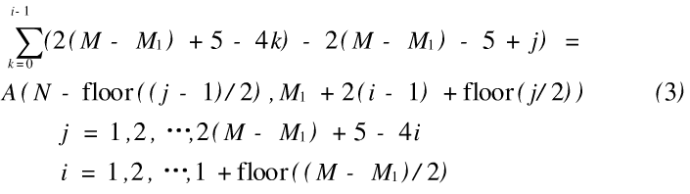
式中,floor(x)表示对x向下取整,mod(x,y)是表示x除以y后获得的余数,以后提到的floor(x),mod( x,y)的定义与此相同。
当N>M时,先对图像矩阵A进行转置变换变成A',然后对A,进行拉伸映射。
转置变换算法为:
![]()
(2)行非邻和列非邻拉伸算法设计
行非邻和列非邻拉伸算法是将图像矩阵行或列的像素插入到其它行或其它列,然后首尾相接形成一个新的向量,实现拉伸。对于维数为N×M的图像,行(列)非邻互插拉伸算法是将第1行(列)同第N行(列)互插拉伸,第2行(列)同第N-1行(列)互插拉伸,后面各行(列)的依次搭配互插拉伸,当N为偶数时中间的两行(列)互插拉伸,当N为奇数时,图像中间一行(列)不经避互插拉伸直接添加到向量尾,图2为6 ×5的图像行非邻拉伸和4 ×4的图像列非邻拉伸过程。
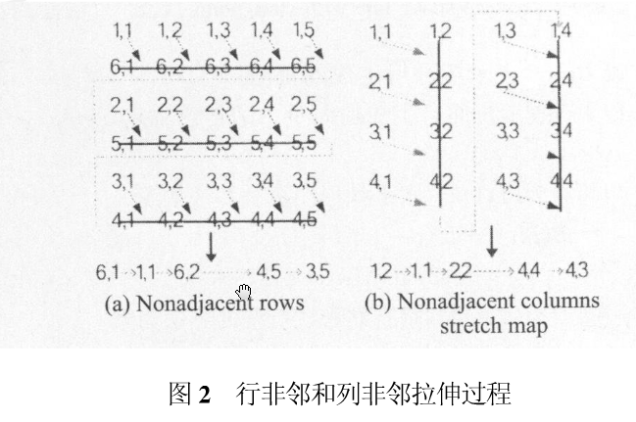
定义奇偶识别函数:
![]()
当x为奇数时,f(x)=0,g(x)=1;当x为偶数时f(x)=1,g(x) =0。
则行非邻拉伸算法为:
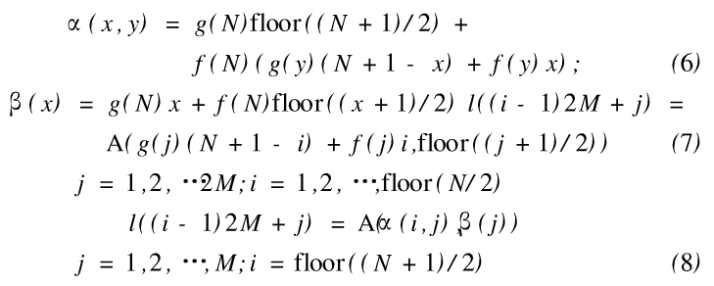
列非邻拉仲算法为:
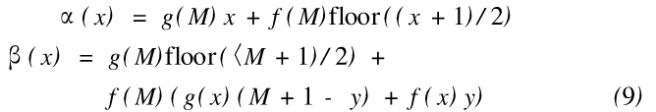
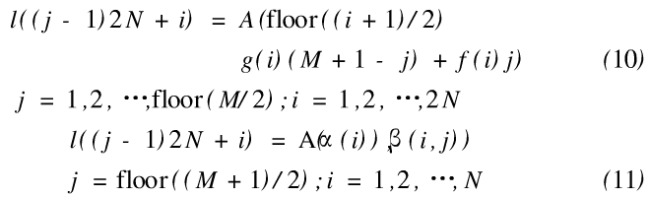
2、折叠算法设计
(1)蛇形线折叠算法设计
将上述拉伸算法得到的向量可以按照蛇形线的顺序进行折叠,得到同样大小的图像矩阵。蛇形线折叠可分为水平、垂直和斜向折叠。
维数为N×M的图像有4个顶点,分别是(1,1)、(1,M)、(N,1)、(N,M)。水平蛇形线折叠可以这4个顶点为起点进行折叠。垂直蛇形线折叠同水平蛇形线折叠类似,垂直蛇形线折
叠根据起始点的不同也分为4种类型,图3给出了起点为f(1,1)的水平和垂直蛇形线折叠过程,以其余3个顶点为起点的折叠过程与此类似。
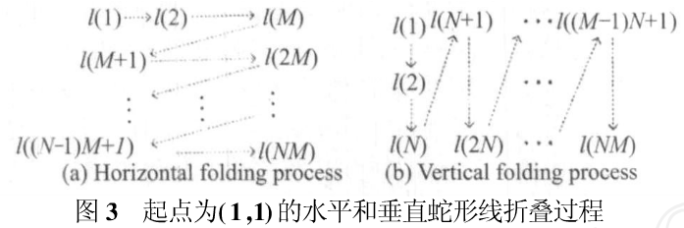
设B(i,j)表示折叠后生成的密图,i=1,2,...,N,j=1,2,...,M。l(i)表示拉伸后生成的向量中的任意一点,i=1,2,...,MN。
当起点为(1,1)时,水平蛇形线折叠算法如下:
![]()
当起点为(1,1)时,垂直蛇形线折叠的算法为:
![]()
以其余3个顶点为起点的折叠算法与此类似,不再详述。
对于1个维数为N×M的图像,从45°方向看去,其图像矩阵是由M+N-1个斜行组成的。1个由N×M个像素组成的向量沿着斜向蛇形顺序折叠,就得到一个N×M的图像矩阵。斜向蛇形线折叠也是根据起点的不同有4种不同的形式,图4给出了起点为(1,1)的斜向折叠过程。与水平和垂直蛇形线折叠相比。斜向蛇形线折射短发推导更加复杂,扩散效率也更好。

当起点为(1,1),且N<M时,斜向蛇形线折叠映射的算法为:
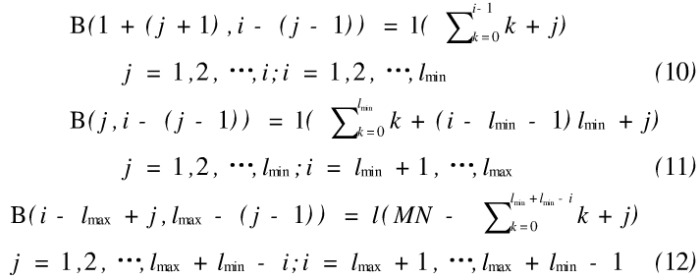
式中,lmin表示M和N中最小值,lmax表示M和N中最大值,下面提到的lmin和lmax。的定义与此相同。以其余3个顶点为起点的斜向折叠算法与此类似。
(2)涡卷折叠算法设计
通过上述拉伸算法得到的向量可以按照涡卷的形状进行折叠得到同样大小的图像。以(1,1)、(1,M)、(N,1)和(N,M)4个顶点为折叠起点,按顺时针和逆时针两种方向,涡卷折叠有
8种形式,图5给出顺时针起始点为(1,1)的涡卷折叠方式。

为使其算法表达简化,定义中间函数如下:

顺时针起点为(1,1)的涡卷折叠算法为:

二、可逆映射集合的图像加密方法
1、可逆映射集合
将前面所提出的各种拉仲和折叠方法进行组合,可建立一个可逆映射集合。在建立可逆映射集合的过程中遵循了方向回避和起始点回避的原则。例如:Line- map属于斜向拉伸,故不与斜向蛇形线折叠组合;行冽非邻拉伸不与水平、垂直蛇形线折叠组合;另外,起始点在(1,1)附近的拉伸算法不与起始点为(1,1)的折叠映射组合。选取了其中4种拉伸映射和5种折叠映射进行组合构成一个具有26种可逆映射的集合,分别用a,b,c,...x,y,z 26个英文字母表示,如表1所示。
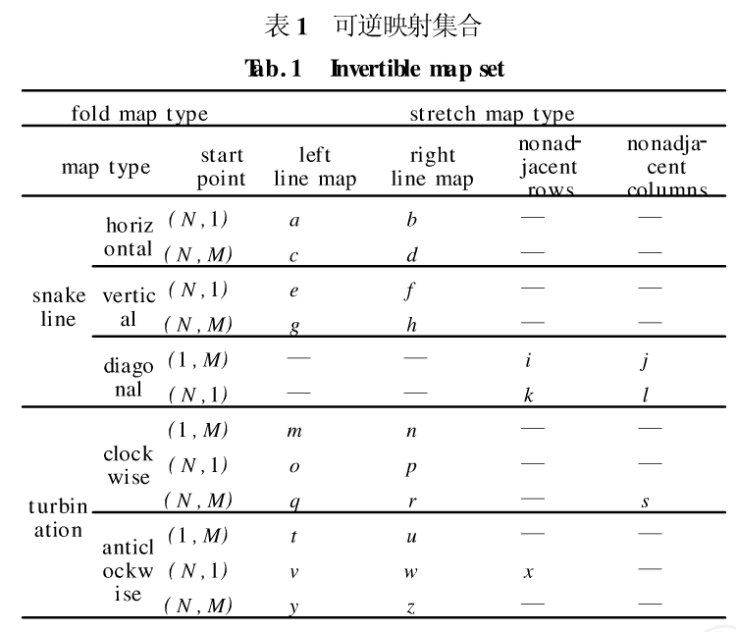
用Z表示可逆映射集合,则Z={a,b,c,...x,y,z},其中,每一种映射都有逆映射,分别用a',b',...,z',表示z'用2表示逆映射集合,则z'={a',b',...,z'}。
2、加密方案设计
对于基于可逆映射集合的图像文件加密方案,密钥设计为集合中映射的种类,也就是密钥用26位英文字母表示,密钥的每一位对应集合中的—种映射方式,每种映射对应的循环映射次数设计为3,然后根据密钥对明文图像做映射循环以完成图像加密,图像的解密是图像加密的逆过程。
下面举例说明加密过程,假设密钥Key=acd,则对像素矩阵A的操作是:读取密钥第1位以,查表1得到以对应的映射种类,即左Line- map拉伸(N,1)起点水平蛇形线折叠映射,则对
矩阵A进行3次该映射得到矩阵Bi:读取密钥第2位c,查表1得到c对应的映射种类,即左Line- map拉伸(N,M)起点水平蛇形线折叠映射,则对Bi进行该映射3次得到B2;读取密钥第3位d,查表1得到d对应的映射种类,即右Line- map拉伸(N,M)起点水平蛇形线折叠映射,则对B2进行该映射3次得到B3。读取密钥完毕,B3即为置乱后的图像矩阵。
三、仿真结果分析
1、图像文件加密和解密
(1)单次映射结果分析
表1中的26种二维可逆映射均可实现对图像像素位置的置乱,首先分别用26种映射对多个不同的原始灰度图像进行了单次映射的加密试验,计算原图和密图相邻像素间的相关系数,加密前后的不动点比等。对试验结果进行分析可知不同映射的加密结果是不同的,其中Line map拉伸同涡卷折叠的组合映射加密的密图的不动点比小于其它映射算法,而且相邻像素间的相关系数也小于其它映射算法,说明该算法的置乱效果较好,而且相邻像素间的相关系数也小于其它映射算法,说明该算法抵御统计攻击的能力较强。
左line map拉伸(N,1)起点水平蛇形线折叠的映射n,行非邻互插后伸(1,M)起点斜向蛇形线折叠的映射a,左line map拉伸(N,1)起点顺时针涡卷折叠的映射0,如图6所示。图6(b)和图6(c)的密图与原图的不动点比分别为0. 54%,0.51%,而密图6(d)与在图的不动点比为0.43%。图6中的4幅图像相邻像素间的相关系数如表2所示,由该表可以看出,o映射密图的相邻像素间的相关系数比a映射和j映射的小。由以上结果可知表1中的不同映射单次映射的加密效果是不同的。

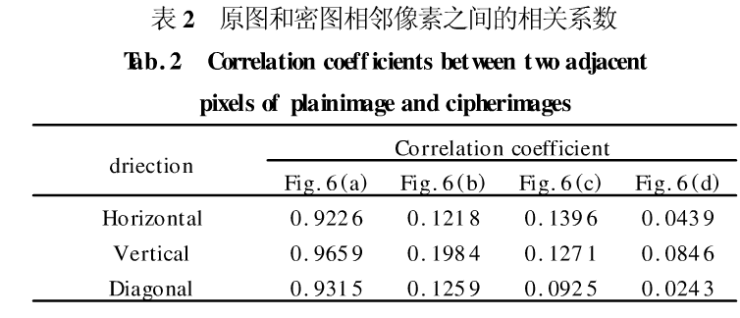
(2)映射的抗攻击结果分析
本文分析了各种映射的抗攻击能力,利用26种映射对多个灰度图像进行单次映射加密,对于得到的密图,尝试用其它映射的逆映射进行解密。结果表明用一种映射对明文进行一次映射置乱后,有可能用其它映射的逆映射完成一定程度的恢复。本文仅以a映射和c映射为例进行说明,用a映射对原图进行1次置乱的加密结果是不安全的,可以用c的逆映射解密进行一定程度的恢复,如图7所示。

大量的加密试验表明,上述问题的解决方案是每种映射对原图循环置乱2次以上,得到的密图就无法用其它映射恢复。如图8所示用口映射对图7(a)的明文图进行循环映射3次后,再用c映射的逆映射无法对密图进行解密。

由此可知,每位密钥对应的循环映射次数量少3次以上才是安全的,即对原图进行循环映射3次以上才不会被其它映射解密所以提出的可逆映射集合的加密方案每位密钥对应的映射次数设计为3。
不同的密钥对图像的加密效果是不同的。当映射次数一定时,分析了采用同种映和不同种映射相互结合加密的密图的相关性值,结果表明同样的映射次数,如果用同一种映射置乱原始图像,得到的密图相关性值偏大;而且不同种映射置乱原始图像,得到的密图相关性值偏小,即其置乱效果更好。即当映射次数相同时,用到的映射种类越多,其置乱效果越好;在设计加密密钥时,应调用尽可能多的二维可逆映射进行加密。
(3)加密方案仿真结果分析
利用提出的可逆映射集合的加密方案对图像进行加密和解密,密钥取为Key=abcdef ghij klmnop,结果如图9所示。

由图9可知,从密文图像中看不出原图的信息,说明该映射加密算法高效地置乱了原图像素的位置,解密后图像与原图完全相同,说明该算法没有信息损失。
2、安全性分析
为了验证提出的加密方案的安全性能,分别对其进行了密钥敏感性分析、密钥空间分析卉目关系数分析和直方图分析。
(1)密钥敏感性分析
密钥敏感性是指在原来的解密密钥Key1基础上做微小的变化,得到Key2,如果用Key2可以对密文进行解密则说明加密算法对密钥的变化不敏感;反之如果无法解密则说明加密算法对密钥的变化敏感,该算法是安全的。
图9(b)的加密密钥为Keyi=abcdef ghij kl mnop,用Keyz=abcdefghij klmnoo和Key3=bbcdefghijklmnop对密文图9(b)进行解密,结果如图10所示,仅对最后—位和第一位密钥值做微
小的变化均不能解密图像,说明该算法对密钥的敏感性较高。

(2)密钥空间分析
由于最基本、最流行攻击密图的方法是对密钥进行穷尽搜索,密钥空间大是加密算法安全的前提。该加密算法的密钥空间与密钥长度的关系如表3所示。

可逆映射集合的加密方案的密钥空间只和密钥长度有关。理论上,在计算速度允许的前提下,密钥长度没有限制,这样可逆映射集合的加密方法的密钥空间可以无限大,保证了加密的
安全性。
(3)相关性分析
由于原始图像相邻像素之间具有很强的相关性,而可逆映射置乱像素后,一个很重要的特性就是改变了原来相邻像素间的联系。如果密图相邻像素之间的相关性变小,说明密图安全性变强。
计算图9的明文图像和密文图像相邻像素的相关系数,结果如表4所示。密文图像相邻像素之间的相关系数比原图的小很多,解密算法很难利用统计攻击方法从密图中恢复原图。

(4)直方图分析
直方图指图像中所有灰度值的概率分布(某一灰度值像素数占像素总数的比率),—般来说,就是图像灰度值的概率密度函数的离散化图形。可逆映射集合的加密方法是通过置乱明文像素的位置来实现加密的,没有改变像素点的像素值,也就是没有改变图像的直方图。利用所提出的加密方案对明文图像进行加密,图11给出了明文图像、密文图像以及它们的直方图。由该图可以看出,明文图像和密文图像的直方图完全相同,直方图信息没有改变,因此密文图像容易被攻击。
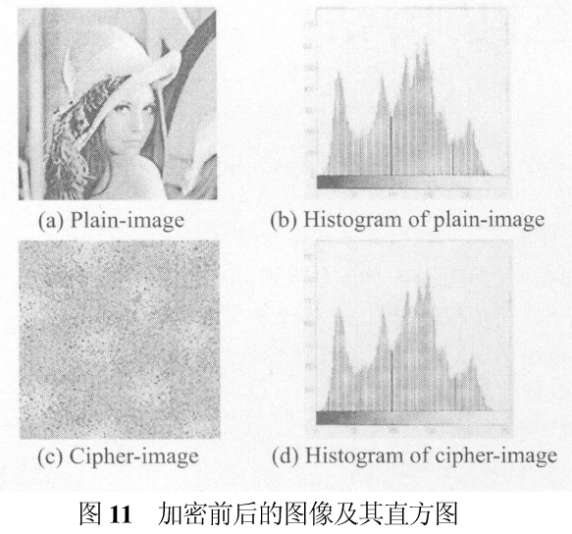
为了隐藏直方图信息,增加相邻4点扩散机制。设图像的大小为偶数,则该图像可以看作是由很多2 ×2的方块构成的新图像。新图像的每一个像素点值,都和2 ×2的方块中的每一个像素的值有关。这样,经过一次迭代之后,被原图像变化影响的像素点有4个。通过这样的过程,就可以达到改变全部或者部分图像像素值的目的,改变原文的一位,都能产生完全不同的密文。从而使得明文攻击无效。
设相邻4点为x(i,j)、x(ij+1)、x(i+1,j)和x(i+1,j+1),扩散后的点为x'(i,j)、x'(ij+1)、x'(i+1,j)和x'(i+1,j+1),则扩散函数为:

增加扩散机制后的密文及直方图如图12所示。在增加了扩散函数之后,为了检验加密算法扩散性,对两个只有1个像素点有差异的M XN的灰度为256的图像进行N PCR(numberof pixels change rate,像素变化率)和UACI(unif'ied averagechanging intensity,归一化平均变化强度)分析。
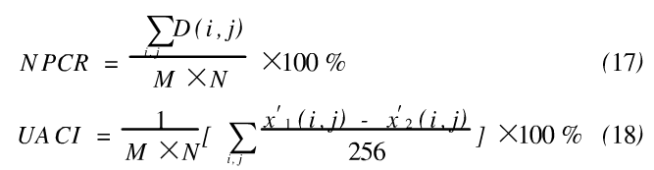
对本文提出的加密方法进行NPCR和UACI分析。采用lenna图做仿真对象,两个密图对应的明文仅有1个像素值不同。计算得到NPCR~1,UACI~0. 35,说明在参数不变的情况下,两个仅有一个像素值不同的原始图像,两个图基本所有的点像素值都不同,且其值变化了35%左右。原图的差别扩散到密图的整个区域,说明扩散效果良好。

为了进一步研究扩散函数的效果,对上述密图做信息熵分析.lenna图的信息熵为7.4255。密图的信息熵分别为7.9892和7. 9826。信息熵和原来的lenna图相比变大了,说明加密后信息熵变大,攻击者从灰度分布中得到的图像信息更少,通过灰度值分析对加密图像进行攻击更难。
小知识之折叠算法
边折叠算法(Edge Collapse)属于几何元素删除法的一种,它的实质是顶点删除。也称边塌陷。.每次简化时,通过算法选定一条有向边e以及相关的2个点(u,v),将其中一个点u“折叠”至v,然后修改拓扑关系,将与u相关的边映射到v,最后完成简化操作。一次简化可以减少源模型的1条边和2个面。









