针对数学公式和化学反应方程式的特点,我们提出了一种适用于数学公式与化学反应方程式的加密方法。该方法首先利用TEX表示方法将数学语言转化成理论计算机科学意义上的语言,以理论计算机科学意义上的语言为桥梁,建立了一种数学语言与自然数序列一一对应的映射,然后设计了一个混沌序列生成器以生成不同的混沌序列,再用混沌序列来加密自然数序列,从而实现数学公式与化学反应方程式的加密。
一、数学公式和化学反应式的混沌序列加密算法相关知识
设有字母表A={s1,s2,…,SN),B={1,2,…,N),定义一个A*→B*的一一对应映射:
![]()
式中:s=a1,a2,...,an,ai∈A,1≤i≤7;f的逆映射为f-l (i)=si。通过映射f,任何字符串信息s=a1,a2,...,an∈A*,可以转换成B上的数组。
字母表A上的连接函数递归定义为:
![]()
而Z= Cn(m)(U1,U2,…,Um)。于是,对于给定的字符串U1,U2,…,Um∈A*,Z= Cn(m)(U1,U2,…,Um)就是把A上的字符一个接一个地连接起来所得到的新字符串。
二、数学公式的转化
计算机科学意义上的语言加密问题已经得到解决,目前有各种各样的对称加密算法和公开密钥加密算法.如果能够把数学的语言,特别是数学公式转换成计算机科学意义上的语言,那么数学公式与化学反应方程式的加密就可以得到解决.尽管数学公式十分复杂,有分式、上下标、括号、分式套分式、上标套上标、括号套括号,但还是可以通过适当的方法来转化它们。采用数学专用处理软件TEX,可以消除数学公式中的一些特有的表示方法,并转换成理论计算机科学意义上的语言,例如,对于公式
![]()
可以表示成:
![]()
根据TEX规则,所有的数学公式都可以转化成这种表示,具体的转化规则请参阅有关TEX的使用说明书。
对于数学公式中的常用符号、函数等,按照便于记忆、便于使用的原则可建立字母表,见表1。

表中的各种运算符、字母以及函数都应当使用它们的TEX表示形式,为了直观起见,以字母的形式直接列入表中。对于没有办法直接表示的符号,如表示分式、向量的\frac、\vec等少量符号,用TEX的表示形式列入表中。称这个字母表为M,那么所有的转化成TEX方式表示的数学公式都可以看作是字母表M上的语言。定义一个集合B={1,2,…,264),然后利用前面定义的映射厂就可以将数学公式转换成一个数值序列。
三、数学公式的加密
1、设计思想
因为序列密码长度可以灵活变化,可以适用于灵活多变的信息环境,所以它是密码学的一个重要分支,发展很快。大量的军事密码系统都是序列密码系统,因此序列密码的设计基本上都是保密的,公开的文献不多。混沌序列具有容易生成、对初始条件敏感、难于预测的特点,混沌序列与随机序列均具有计算上的不可区分性,所以混沌序列加密方法是目前图像文件加密中使用得最多的力密方法。本文设计了一种利用混沌序列函数生成混沌序列的算法,然后将混沌序列与前面转化成的数值序列进行异或运算,从而实现对数学公式的加密。
假设有一个离散序列函数:
![]()
该函数具有如下性质:
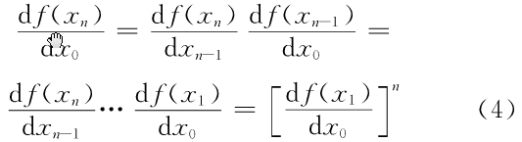
又假设有一个序列X由初值xo迭代生成,另有一个序列X'由初值x=xo +dxo迭代生成,那么Xn和Xn'的差:
![]()
式中:L称作Lyapounov特征指数:
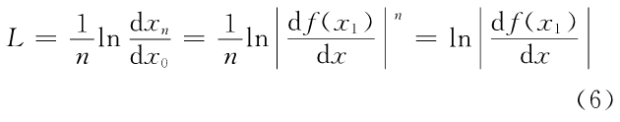
如果|df/dx|>o,那么L>o。给x0一个微小的变化,经过行次迭代,x0将指数分离。也就是说,迭代结果对于初始条件是极度敏感的,这样的结果将导致混沌。经过n次迭代,f(x0)已经与初值xo没有确定的关系,结果将是不确定的,即发生了混沌。如果选择一个足够大的愚k,令{Xk+l,Xk+2,…,Xk+n)={X1,X2,…,Xn)=X,序列X将是不可预测的。
虽然这样的混沌序列无法从初值预测序列的Xi,但是知道了Xi,则可以预测Xi+1,对这样的混沌序列作进一步的数学处理,使得即使知道了Xi,也不能预测Xi+l,从而生成一个随机的混沌序列.令Yi=(aXi)mod m,y用于加密数据文件,这样即使攻击者获得了K,它仍然无法预测Yi+1,因为Yi+1=g(Xj+4)而与Y没有函数关系,根据所断言的不可预测性与随机性的关系可知,序列y是随机的,选择:
![]()
因为式(7)所表示的离散序列函数可以等价地记作:
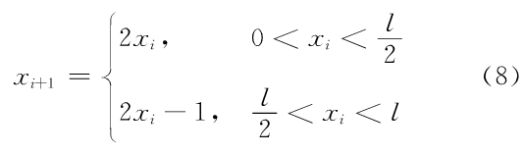
由于:
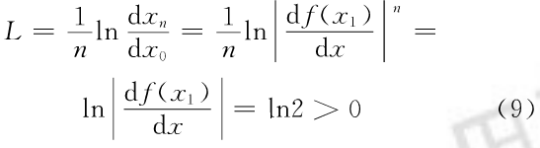
满足生成混沌的条件.选择一个充分大的k,计算出序列(Xk+1,Xk+2,…,Xk+n),利用该序列,通过函数Xi=(axk+i)mod m生成序列X={X1,X2,…,Xn).将序列X与由数学公式转化来的数值序列进行异或运算,就完成了数学公式的加密。这里有一个技巧就是如何选择合适的序列种子c,使得攻击者无法分析c。
2、数学公式和化学反应式的混沌序列加密算法描述
(1) Alice将数学公式转化成计算机科学意义上的语言,再利用式(1)定义的映射把语言中的字符串转换成数值序列,并设这样的序列为{f(m1),f(m2),…,f(m2n)}(如果直接转换过来的序列不是偶数,可以用零填补),利用函数Pi=CN(f(m2i-1,f(m2i))将序列转换成长度为行的序列。
(2)Alice选择a、k、l、m和2个大素数p、q,令xo =c=p/q,利用式(8)生成序列{Xk+1,Xk+2,…,Xk+n),再利用函数Xi=(axk+i)mod m(i=1,2,…,n)生成序列X= {X1,X2,…,Xn)。
(3)C(C1,C2,…,Cn)={P1+X1, P2+X2,…,Pn+Xn),并用Bob的公开密钥加密a、k、l、m和2个大素数p、q,得到(Eb(a),Eb(l),Eb(k),Eb (m),Eb(p),
E6(q))。
(4)Alice将C和(E6(a),(Eb(a),Eb(l),Eb(k),Eb (m),Eb(p),E6(q))都通过公开信道传送给Bob。
(5) Bob收到这些密文层,首先解密出a、k、l、m、p和q,重构序列X={X1,X2,…,Xn),然后解密消息的密文C={C1+X1,C2 +X2,…,Cn+Xn)。
(6)Bob利用P运算M=CN (P1,P2,…,Pn),然后将M放在TEX的编译器中进行编译,就可以恢复出最初的数学公式。
四、数学公式和化学反应式的混沌序列加密算法分析
一个算法的安全性取决于密钥的安全性,要想彻底了解本算法的安全性,首先需要了解伪随机性与不可预测性的关系。
定义 对于序列X1,X2,…Xm,…|X|=max( |Xi |(1≤i≤m)),如果对于每一个概率多项式时间算法D,都有:
![]()
式中N表示字母表中符号的个数,则称序列X1,X2,…,Xm,…是不可预测的。本方案的序列X就满足这样的特性,序列中的前i项与第i+1项并没有直接的联系,所以知道前i项对于预测第i+1项并没有帮助,因为第i+1项是由另一个序列的i+1项生成的.要能够猜测出另一个序列,可以归约到攻破公开密钥体系,在不能攻破公开密钥体系的条件下,本方案中所用的加密序列是无法预测的。因为该序列是伪随机的,随机序列与任何序列的异或仍然是随机序列,所以密文序列与随机序列是无法区分的,从而可以认为该密文序列是安全的。
另一方面,对称加密密钥是一次性的,类似于一次一密通信。Shannon已经证明一次一密是绝对安全的,这也说明了本方案的安全性。本方案的安全性最终归结为公开密钥体系的安全性。公钥加密算法的安全性是基于攻击复杂性的安全性,使用较长的密钥就可以获得较高的安全性,而本方案中由于用公钥加密的只是简单的密钥种子,所以可以选用较长的密钥而不影响加密的速度,同时可以保证较高的安全性。所以,利用本文的混合密码系统加密数学公式既保证了安全性,又保证有较高的运算速度。只要建立适当的字母表,这种方法可以很容易地推广,以用于化学反应方程式的加密。
小知识之TeX
TeX是由著名的计算机科学家Donald E. Knuth(高德纳)发明的排版系统,利用Tex很一很容易的生成高质量的dvi文件,打印输出。利用dvips,dvipdfmx,pdflatex等程序生成pdf,ps,文件,latexhtml生成html文件。 它在学术界十分流行,特别是数学、物理学和计算机科学界。TeX被普遍认为是一个很好的_排版工具,特别是在处理复杂的数学公式时。利用诸如是LaTeX等终端软件,TeX就能够排版 出精美的文本。通过ctan上的宏包可以扩展其功能,可以作幻灯片,定义模板。中文支持可以由CCT,CJK来完成。











