admin 随着计算机和通信技术发展，多媒体数字图像信息的安全性逐渐成为人们关注的焦点。传统的加密算法因密钥量较小，难以抵抗穷举攻击，同时对剪切、噪声攻击的抵抗力也较弱。为此，我们从增大加密图像熵角度引出分块均匀加密方法，进而结合混沌映射提出一类基于仿射模变换的均匀加密算法对图像文件进行分块加密。
一、数字图像的仿射模变换与分块均匀加密
1、仿射模变换
设（x，y）是一个N×N图像的原始像素点坐标，（x'，y'）是图像置乱后的像素点坐标为：x，yx'，y'∈{1，2...，N}。如式( 1)所示变换类型称为仿射模变换：
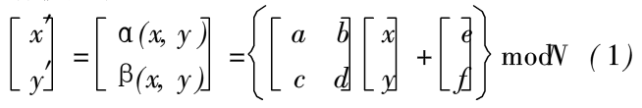
式中：参数a，b，c，d，e，f不为0，作为加密密钥；mod是取模，即求余，目的是为了保证变换后像素点仍落在原先的图像区域内。若矩阵行列式
，则该变换为保面积映射，是一对一映射可用于图像置乱且由于
与N互素，仿射模变换具有周期性加密若干次后恢复原始图像又由于仿射模变换是对图像整体进行几何位置置乱只加密1次效果并不理想，因此本文给出分块均匀加密方法。
2、分块均匀加密
图像加密即图像置乱的实质就是要降低像素点位置之间和像素值之间的相关性直至无关，从信息论的角度数字图像可以看作是由任意形状和数量的不相交块区域组成的数字信息源，图像的每个像素可以看作信息源中发出的消息。图像置乱的过程可以看作是减小图像相邻像素相关性的过程同时也是增大图像像素分布不确定性的过程，即增大图像信息量的过程。实际的自然图像像素在各个分块区域内的相关性可以看作最大，即确定性最大。若置乱前原始图像同一分块区域σ1内的一些像素点在置乱后还分布在同一分块区域σ2易即使σ1和σ2位置不同，这些像素点的确定性仍旧较大，相应地通过置乱产生的信息量增加幅度较少。因此提出图像位置熵的定义：
式中：B是图像分块区域个数，Hk(p)为第k个分块区域信息熵表示第k个分块区域平均位置信息量。
式中:P (i，j)表示原始图像坐标为_(i，j)的像素在置乱后图像第k个分块区域出现的概率。由离散信源熵的性质，当P(i ，j)等概时熵函数Hk(P)最大，从而位置熵H(R)最大。也就是说理想的置乱状态是置乱图像中任意分块区域内的点来自原始图像各个位置的概率都相等或者说原始图像同一分块区域内的点分布到置乱图像不同分块区域的概率相等，则置乱后图像信源的平均信息量最大，置乱效果最好。为达到理想的置乱效果提出如下均匀置乱方法：如果原始图像中每块所有点分别出现在置乱后图像的全部分块中，且不管这些点在置乱后图像各块中出现顺序如佩要保证每块中各含有一个点f而置乱后图像每块中所有点都来自原始图像的不同块中，就称为均匀置乱。图1为16 ×16图像分块均匀置乱（加密）示意图，置乱前后图像都分为4×4块，置乱前图像第1个分块内的点分布在置乱后图像的各个块中。
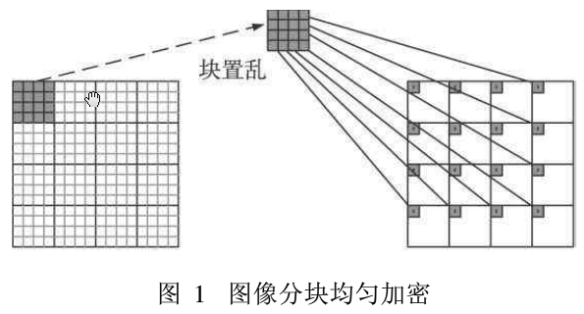
按照上述原则，N×N方形原始图像，其理想状态分块数应为N×N块。但对于不同大小图像来说，这个值不一定为可以实现均匀分块的整数可以将与这个值相近的两个数作为理想的分块数。
二、基于仿射模变换的分块均匀加密算法
1、算法基本原理
为把分块均匀加密方法应用于仿射模变挽需要对该类变换进行改进使其从局部位置映射到置乱后整幅图像。对第(i,j)个分块，该分块内的仿射模变换为：
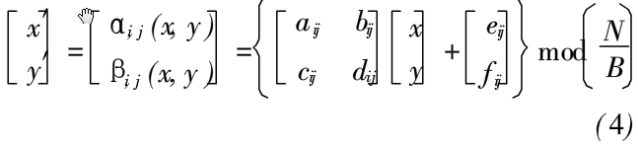
式中：N代表图像大小为N×N；曰是原始图像分块数即分为B×B块；aij,bij,cij,dij,eij,fij为每一个分块的参数，且满足保面积映射要求：ij∈(1B)，取正整数，则采用分块均匀置乱的仿射模
变换为：
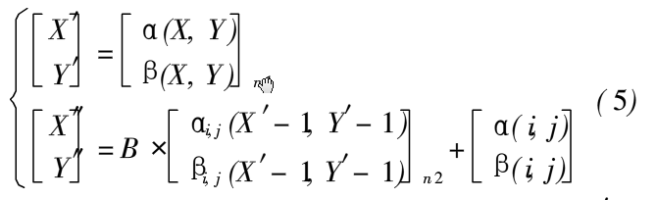
式中：x和y表示原始图像的像素点坐标；x'和y'表示对原图做整体置乱后的像素点坐标；x'‘和y’‘表示对整体置乱图像再进行分块置乱后的像素点坐标，n1和n2为迭代次数。该公式表示先将图像进行n1次整体仿射模变挽在图像像素点位置充分打乱的情况下，再根据分块均匀置乱进行n2次加密。若n1=0则表示直接对图像进行分块均匀置乱。可以将aij,bij,cij,dij,eij,fij都作为密钥，由于每一分块的参数都不同，所以该算法的密钥量是足够大的。但置乱的时候就需要记住每个分块的参数值，这显然是不切实际，可以通过引入混沌映射来解决这一问题。
二、改进的Logistic映射
Logistic映射函数式如下：
式中：0<μ≤4为分支参数，xn∈(0,1)。当3. 569 945 6<μ≤4 Logistic映射处于混沌状态，但一般取μ=4的混沌系统，为图像文件加密操作提供了很好的技术保证。但Logistic映射当0< x<1时不满足均匀分布，为了得到随机性更好的均匀分布的随机系统可将式(6)作如式（7）所示变换：
序列yn同样是混沌序列，且分布具有均匀性。利用改Logistic混沌映射的无规则序列，通过对序列yn的每个值进行放大、取整、取余等数学变化，可以将其作为式（5)的每个分块的参
数值。
3、基于仿射模变换的图像分块均匀加密算法步骤
（1）加密步骤
*给定Logistic混沌映射的6个初值为X1（0）、X2（0）、X3（0）、X4（0）、x5（0）和X6（0）上按照置乱所需参数的个数产生6个混沌序列{xn(k)|n=1,2…,6,k=0,1,2...}将这6个混沌序列按照式(7)改进为{yn(k)|n=1,2…,6,k=0,1,2...}将这6个改进序列小数点后第二位和第三位取出组成十进制数从而得到4个十进制序列{a(k)}{b(k)}{c(k)}{d(k)}{e(k)}{f(k)}整6个序列的值分别作为各分块中用到的参数aij,bij,cij,dij,eij,fij。如果aij,bij,cij,dij满足保面积映射约束条件则进行下一步，否则将dij自加1，直到满足约束条件为止。
*对图像F(x,y)做a=a(0),b=b(O),c=c(0)，d=d（0)，e=e(0），f=f(0)的仿射模变换，迭代n次产生图像F’(x',y')。
*将图像F’(x',y')分成B ×B块，依次将混沌序列的{a(k)}{b(k)}{c(k)}{d(k)}{e(k)}{f(k)}带入式（5），迭代n2次，得到密图F’'(x'',y'')，完成图像的加密。
（2）解密步骤
*同加密步骤( 1)；
*求出不同a、 b、c和d值周期的最小公倍数T2，令n22=T2 -n2；
*将密图F’'(x'',y'')分成N2/B2块，依次将混沌序列的{a(k)}{b(k)}{c(k)}{d(k)}{e(k)}{f(k)}带入式（5），迭代n2次得到图像F’(x’，y')；
*对图像F’(x’，y')进行仿射模变换，其中a=a(0),b=b(O),c=c(0)，d=d（0)，e=e(0），f=f(0)歹迭代n1次，即可得到原图像，实现解密。
小知识之图像熵
图像熵表示为图像灰度级集合的比特平均数，单位比特/像素，也描述了图像信源的平均信息量。
