彩色图像处理是数字图像处理的重要组成部分,在网络与多媒体通信中,常常涉及到彩色图像文件加密。为此,我们提出了一种彩色图像混沌加密算法,该加密算法通过选用Lorenz系统中三个不同维的变量生成置乱矩阵来分别实现对RGB彩色图像三分量的置乱加密,从而实现对整个彩色图像文件加密。
一、彩色图像混沌加密算法设计实现
1、对Lorenz混沌序列的优化
Lorenz动力学方程为:

其中, 参数σ,r,b 的典型值分别为σ= 10,r=28,b=8/3,在σ和b不变,当r>24.74时,系统进入混沌状态。
但该系统输出的实值混沌序列有一些固有缺陷:x,y,z的值域各不相同,不利于批处理;x,y,z局部取值呈现单调性,易受线性预测攻击;x,y,z自相关特性非理想的δ函数,互相关特性非理想的零特性,难以保证不可预测性,而且系统多输出特性也得不到充分利用。为此,有专家提出了一种对Lorenz混沌序列的优化方法,构建了式(2)所示的一个数学模型:

其中,x',y',z'三为优化后的实值混沌序列;m为控制参数,通过它可以提高序列取值的不规则性;round()为取最接近整数函数。经过实验,证明此优化序列具有良好的混沌特性、较理想的万函数自相关特性和近似为0的互相关特性。
本空域算法采用了此混沌优化序列。
2、置乱算法
利用式(2)产生的三个优化后的混沌序列x',y',z'生成三个置乱矩阵,分别对RGB彩色图像的三个分量进行置乱加密。
置乱矩阵的生成方法:利用优化混沌序列生成相应的置换矩阵PM×N, 对PM×N来说, 其中任一元素Pij∈[1,2,…,M×N],且Pij=Pkl,当且仅当i=k,j=1。
比如:M=4,N=4,P即为4×4的矩阵,由优化混沌序列生成16个实数值组成的混沌序列为:
10.95621370、10.91248372、 10.57640346、11.0759704、11.62504738、 11.13958961、 10.26628130、 9.10829136、9.53332571、 9.21575219、 9.11570905、 9.19910548、8.87154601、9.27423505、 9.85781001、10.94356727
对以上序列按大小排序,然后从1到16进行标识,即可得到序列:4、6、7、3、1、2、8、15、10、12、14、 13、16、11、9、5。
按行排列成4×4的置乱矩阵P4×4为:

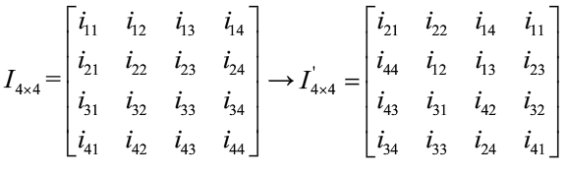
置乱规则:采用非线性置换方法,将图像IM×N。N与置乱矩阵PM。Ⅳ的元素一一对应。将IM×N中的元素对应PM×N中的元素进行置乱。如对4x4的图像I4×4按照上面的P4x4矩阵进行
置乱,I中的第1个元素移到第4个元素位置,第2个元素移到第6个元素位置,…,具体过程为:
3、分块加密
由于经本加密算法加密的彩色图像在以后的处理过程中还要进行JPEG压缩,而JPEG压缩过程中的二维DCT、系数量化以及熵编码都是以8×8块为基本单位进行的,为了不破坏DCT系数的分布概率,并且使Huffman编码表能按最优方式使用,我们将待加密彩色图像的R、G、B3个分量按8×8大小分块,以8x8块为单位分别用置乱矩阵Px,Py,Pz进行空域置乱加密。
4、彩色图像混沌加密算法的实现
(1)彩色图像混沌加密算法的实现
图像加密算法实现步骤为:
Step1:输入待加密的彩色图像,分离彩色图像的R、G、B三基色分量。
Step2:对Lorenz混沌序列进行优化处理。输入密钥σ,r,b,x0,yo,z0(xo,yo,zo为初始值),生成x,y,z实值混沌序列,用式(2)对x,y,z混沌序列进行优化,得到x',y',z'优化混沌序列。
Step3:将待加密彩色图像的R、G、B3个分量按8x8大小分块,以8×8块为单位生成置乱矩阵Px,Py,Pz。
Step4:空域置乱。按置乱矩阵Px,Py,Pz规则重排三基色分量8×8块的几何位置,实现置乱加密。
Step5:输出置乱彩色图像。合成置乱后的三基色图,即得到加密后的图像。
(2)解密算法实现
用户输入正确的密钥后,将加密算法逆向运算,即可获得解密图像。
二、实验仿真
我们选取大小为512×512的彩色图像Lena作为实验对象(如图1),利用MATLAB 6.5编程实现算法。选取密钥σ=10,r=28,b=8/3,xo=0.5143978026,yo=0.3246981507,
zo=0.7021364589。为了增强生成混沌序列的安全性,我们除去序列的初始段,使Lorenz方程预先迭代n=10000次。
图2、图3、图4分别是Lena的三基色分量分解图,图5、图6、图7分别是三基色分量图加密后的图像,图8是将分量图合成为彩色图像后的Lena最终加密图像。

三、安全性分析
1、保密性测试
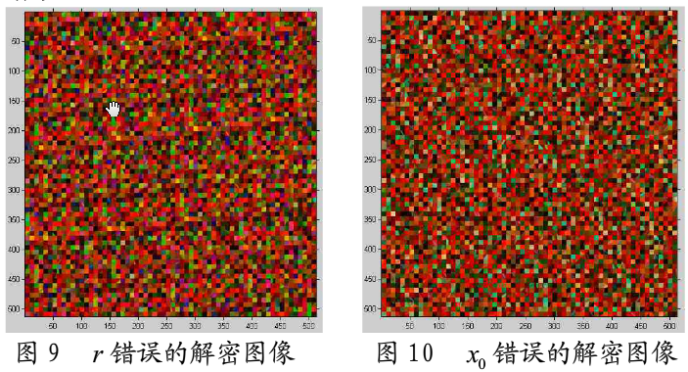
本算法在空域范围内使用Px,Py,Pz对彩色图像三基色分置乱,从密码学角度来说,加强了算法扩散的强度。若采取唯密文攻击,则解密工作量高达3×(M×N)!,进一步加大了破译难度。另外,三基色分量分别置乱,混淆了彩色图像每一像素的R,G,B三分量,使加密图像在视觉上发生了色彩变化,图像更难读懂。图9为参数r的偏差为10的-10次方时的错误解密图像,图10为初值xo的偏差为10的-10次方时的错误解密图像。
由于混沌序列对系统参数和初值极其敏感,即使密钥有微小的变化也会得到完全不同的置乱矩阵,从而导致错误的解密结果。
2、置乱度分析
我们使用置乱度(SM)来评估加密图像的置乱程度。它的计算式为:
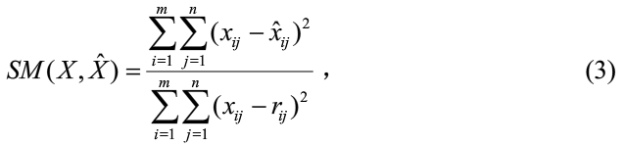
在本加密算法中,我们将R定义为经过幻方变换生成的置乱图像。幻方变换是一种矩阵变换,在图像文件加密中,它的加密算法和密钥是不能公开的,因此,一般不单独作为加密算法。但单就置乱效果而言,幻方变换的置乱效果是很好的,所以我们将它作为衡量本加密算法置乱度好坏的一个标准。
我们利用本加密算法多次试验来计算Lena三基色分量图像的置乱度,可得到SM的平均值SM为:

可见,本加密算法的置乱度与幻方变换的置乱度相近,具有良好的置乱性。
3、抗攻击测试
图11、图12分别为Lena加密图像受到压缩处理、噪声干扰后的解密图像。图1 1为加密图像经JPEG压缩为原大小20%后的解密图像,图12为加密图像受到10%强度的高斯噪声干扰后的解密图像,可以看出解密图像效果较好,具有较强的抗攻击能力。

小知识之Huffman编码
哈夫曼编码(Huffman Coding)是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫作Huffman编码。











