为了实现图像安全,快速给图像文件加密,我们利用了图像像素可以插入到相邻像素之间以及拉伸折叠的思想设计了一种基于三维坐标的图像加密算法。
一、把二维十进制矩阵转化为三维二进制矩阵
对二维图像的处理一般是把数字图像读成N×M分别为原二维矩阵的长和宽,K为十进制数转化为二进制数后的二进制位数。如下图1所示:
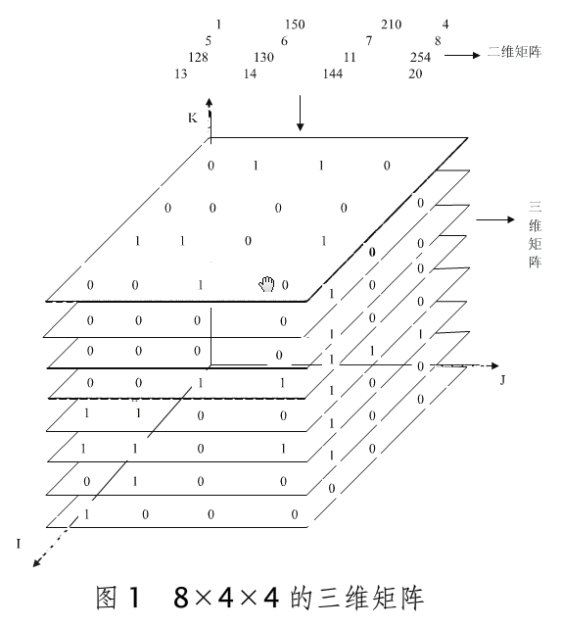
二、映射思想
设三维矩阵在在IJ坐标的投影上一个N×N二维矩阵(当投影不是N×N的方阵时,可以用插补法把它补成投影时是方阵),新映射方法就是根据图像像素能够插入到其他相邻的像素之间的性质。根据方向的不同,映射分为左映射跟右映射。
首先把三维矩阵沿平行于K轴,沿着IJ平面的对角先把三维矩阵切开,分成左右两部分。左映射就是在IJ平面上,把左半边矩阵从左到右第一行的所有元素依次插入右半边矩阵从上到下的第一行两个元素之间,并且保持K轴坐标不变。然后再把左半边矩阵从左到右第二行的所有元素依次插入右半边矩阵从上到下的第二行矩阵中,并且保持K轴坐标不变…重复以上过程,直到取完左半边的数据,如图2所示。
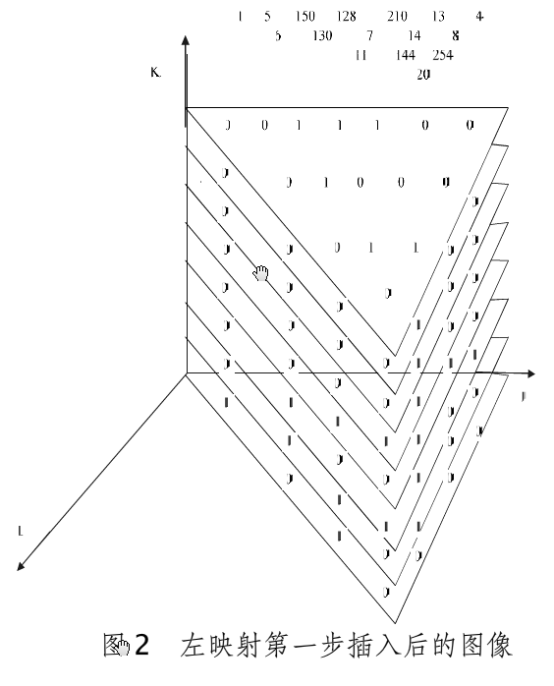
第2步就是把在IJ平面上第二,三,N行的对应的平行于K轴平面依次添加到第一行的平行于K轴的平面后面,这样三维矩阵就转化成为了一个的二维矩阵,如图3所示。

最后对二维矩阵进行置乱,然后把矩阵还原为原来的8×N×N矩阵。
其中除了最后一步对二维矩阵进行置乱之外,前两步中,数据保持K轴不变。右映射与左映射相似,而且是相对称的。就是首先把右半边IJ平面上第一行的元素分别插入到左半边第一列的两个元素之间,然后是第二行…,第三行…。
第2步就是把平行于K轴的,第2,3,…列所在的平面的二维矩阵沿K轴依次添加到第一行所在的平面的矩阵后面。
最后就是对生成的二维矩阵进行置乱,并且把矩阵还原为原来的8×N×N矩阵。
1、映射的计算算法
设图像读成8×N×N的三维矩阵A(k,i,j),iJ=0,1,…,N一1,k=0,1,…,7,P(k,m),m=O,1,…,N2_1,k=0,1,…,7;为将A(k,i,j)拉伸为一个平面后的二维矩阵o(下文的k,iJ,m取值范围同上)左映射计算算法如下:
当i>j时,有:
![]()
当i<=j时,有:
![]()
右映射计算算法为:
当i>j时,有:
![]()
当i< =j时,有:
![]()
把二维矩阵P(k,m)折叠成为三维矩阵B(k,i,j)的折叠算法为:
![]()
三、图像文件加密和解密原理
将左映射和右映射的映射次数设计为密钥Key,其中当取Key的值是第奇数位时,映射为左映射,且映射次数为Key的位数数字的值,同理,当取Key的值是第偶数位时,映射为右映射,且映射次数为Key的位数数字的值。例如Key=2345表示先左映射2次,然后右映射3次,再左映射4次,最后右映射5次。
1、图像文件加密过程如下:
①把二维图像读成三维二进制矩阵,设置好密钥Key;
②取出Key的—位数字,并根据数字位置跟数字和式(1)一(4)将图像三维A(k,i,j)转化成二维图像p(k,m);
③用图像置乱算法将二维图像p(k,m)置乱;
④根据折叠法(式(5)把二维矩阵p(k,m)折叠成为三维矩阵A(k,i,j),继续取出Key的一位数,重复①;
③步直到取完Key的位数;
⑤把最后生成的三维二进制矩阵读成二维十进制矩阵;
2、文件解密过程如下:
①从未位读起读取Key的一位数字,并且把二维矩阵图像读成三维A(k,i,J);
②把三维矩阵A(k,i,j)拉着一个二维矩阵p(k,m);
![]()
③根据图像置乱算法的解密算法把p(k,m)解密,并且根据读取的是Key的第几位数值和数值的大小,来判断加密是左映射还是右映射和解密次数。如果加密时是左映射,则解密方法如下:
当i>j时,有:
![]()
当i<=j时,有:
![]()
如果图像文件加密时是右映射,则解密方法如下:
当i>j时,有:
![]()
当i<=j时,有:
![]()
④继续读取Key的数值,重复(2),(3)步,知道读取完Key的位数。
⑤把最后生成的三维二进制矩阵转化为二维十进制矩阵,则其对应的图像为所求的解密图像。
四、图像文件加密和解密实例分析
1、图像文件加密实例
本文在图像文件加密过程中的第3步对二维图像p(k,m)是基于改进的Logistic映射。
对L= 256的Lena灰度图进行加密。当Key1=1, Key2=01, Key3=123456778和Logistic映射中xo =0.556465656,β=3.943534534534时,图像文件加密效果如下图所示。
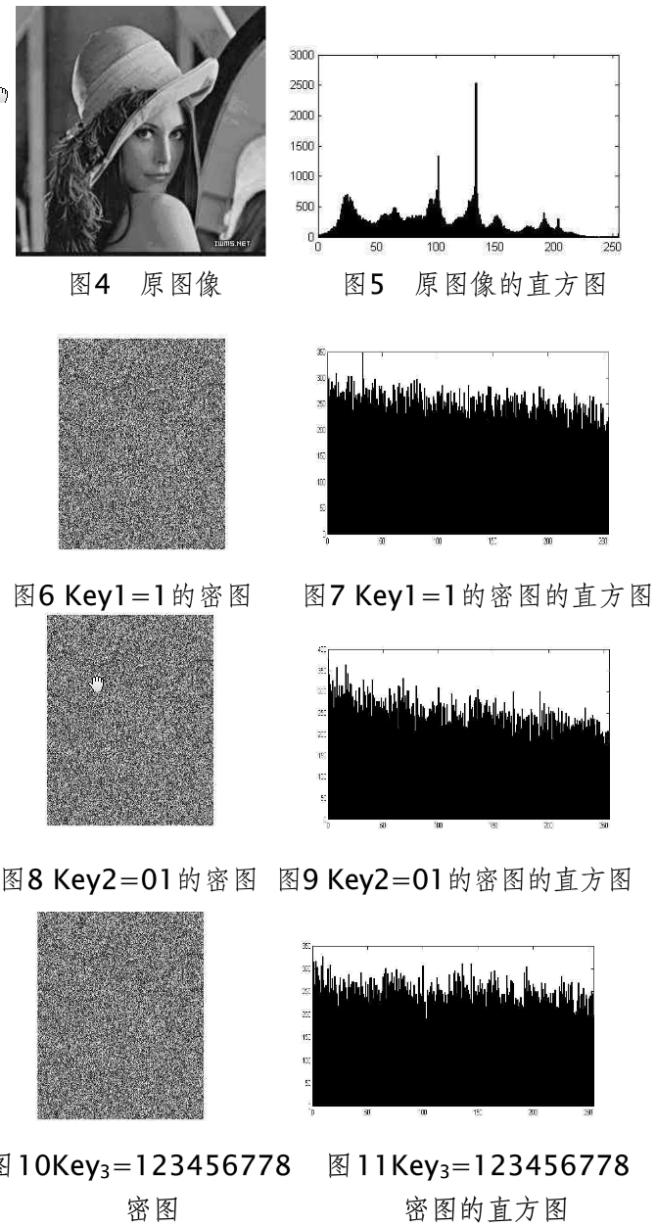
由图5,图7,图9,图11可以看出,利用本文提出的加密算法加密的密图的直方图与原图的直方图是不同的,这说明这种加密算法不仅改变了像素的位置还达到了改变图像像素的效果,隐藏了直方图信息,可以有效的抵御已知(选择)明文攻击,提高了加密算法的安全性。
2、安全性能分析
本加密算法中涉及了左右映射跟改进的Logistic映射,其中左右映射的密钥空间只与密钥长度大小有关他们之间的关系如下表1:
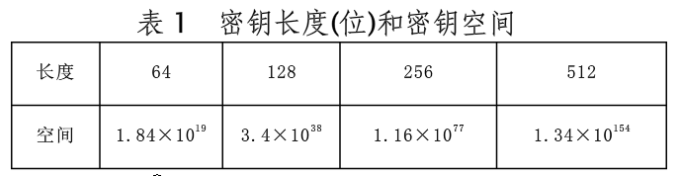
密钥敏感性分析。对用Key=123456778对图像文件加密,然后分别用Key1=123456777,Key2= 123456779和正确的Logistic映射密钥进行解密,如图1 2,1 3所示。即使加密密钥和解密密钥仅有非常小的差异,也无法解密图像,加密算法对密钥变化非常敏感。

统计分析:原始图像中相邻像素的相关性是很大的,为了破坏统计攻击,必须降低相邻像素的相关性,对图像中像素点相邻点进行相邻点分析。
通过相关系数的计算方法计算,相邻点的相关系数如表2。
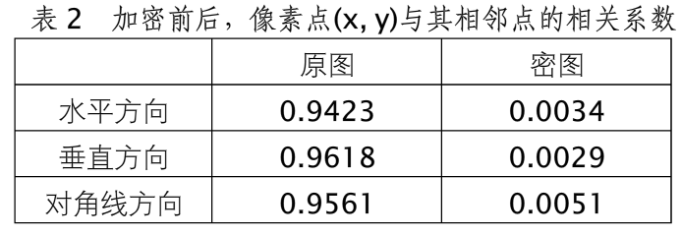
显然,图像文件加密后,密图像素值与相邻点像素值之间的相关系数非常小,解密算法很难利用统计方法从密图中恢复原图。
最后计算分析原图和密图的不动点比o原图像A的像素点A(iJ),在加密后其图像灰度值没有发生变化,则称该像素点为不动点。图像中不动点占有像素的百分比称为该图像的不动点比。在Key=l时,即图6跟图4的不动点比为0.404%; Key=01,即图8跟图4的不动点比为0.407%。这说明只在一次左映射或者右映射的情况下,不动点的数目很少,99.5%以上的像素点都发生了改墨,置乱效果很明显。
最后计算分析原图和密图的不动点比。原图像A的像素点A(i J),在加密后其图像灰度值没有发生变化,则称该像素点为不动点。图像中不动点占有像素的百分比称为该图像的不动点比。在Key=1时,即图6跟图4的不动点比为0.404%; Key=01,即图8跟图4的不动点比为0.407%0这说明只在一次左映射或者右映射的情况下,不动点的数目很少,99.5%以上的像素点都发生了改变,置乱效果很明显。
五、新映射与其他混沌映射比较
Baker map是最典型、应用最广的混沌映射之一,在图像加密领域得到广泛的应用。新映射和Bakermap比较:
①密钥空间更大。Baker map有两种形式,但即使是Baker map的一般形式(即密钥不是图像大小的因数的情况),Baker map的密钥空间最大仅为2N-1(N为图像的宽),而新映射的密钥空间只和密钥本身长度和改进的Logistic映射有关。只要计算速度允许,密钥长度没有限制。
②对密钥变化更加敏感。新映射只要密钥稍有变化,密图就会截然不同。因此,用相似但不相同的密钥无法对密图解密。而使用相似的密钥也可以对Baker map加密密图进行解密。
③改变图像的像素值,由图5,图7,图9,图11可知,本算法可以改变原图像的直方图,即本加密算法可以改变图像的像素值,这样可以有效的隐藏直方图信息,从而抵御己知(选择)明文攻击,提高加密算法的安全性。
六、基于三维空间下的图像加密算法优点
本文提出了一种基于三维空间下的图像加密算法,算法具有如下优点:
①公式非常简单,容易编程实现。
②映射是可逆的。
③在加密/解密过程中没有信息损失。
④加密的密钥基本没有限制。
⑤密图和原图大小一致,没有大小差异。
⑥能满足实时需要,适合大尺寸图像文件加密。
⑦经过映射后,可以改变原图像的直方图。
⑧加密算法简单,容易硬件实现。
小知识之三维空间
三维空间,也称为三次元、3D,日常生活中可指由长、宽、高三个维度所构成的空间。而且日常生活中使用的“三维空间” 一词,常常是指三维的欧几里得空间。










