面包师变换是动力系统中一个非常经典的变换,为了对图象文件加密,Masaki_Miyamoto等人把面包师变换推广到截断面包师变换情形,并给出了基于位置的图象文件加密方法,那么今天,我就给大家介绍一下这种基于面包师变换的数字图象加密技术。
一、二进制下的面包师变换
1、面包师变换
面包师变换B(1/2,1/2)是Bernoulli推移的推广,它定义为如下映射T:

其中(Xk,Yk)表示某个初值经过k次映射后的值,显然T是可逆的,它的逆映射为:
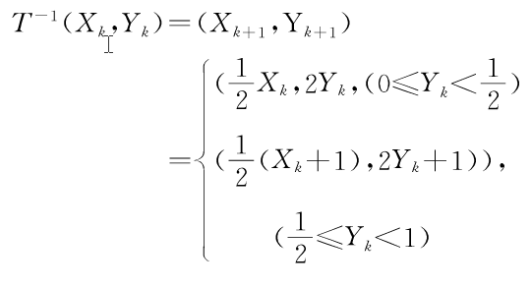
假设(Xo,Yo)∈M,其二进制序列为:
![]()
其中:
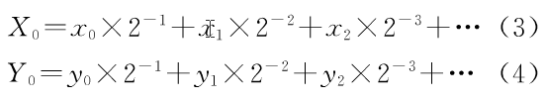
则面包师变换T等价于推移算子Φ:
![]()
即二进制序列向左移一个字节,由于T同构于Bernoulli推移,所以它具有遍列性质和混合性质。
2、二进制截断面包师变换
为了定义二进制截断面包师变换B*(1/2,1/2),其变换的原空间M*通过把M*[o,1)2划分成2l×2l个部分而得到,记为M*=[o.2 l-1]2,(l=O,1,2,…)。
二进制截断面包师变换T*定义如下:
(1)当0≤Xk<2l-1时,
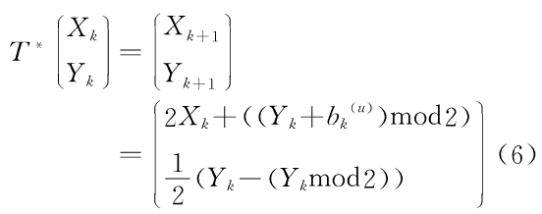
(2)当2l-1≤Xk<2l时,
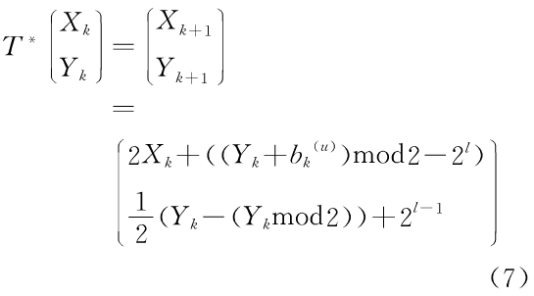
其中(Xk,Yk)表示M*上k次迭代的值。而:
![]()
是一个二进制随机序列,u表示数列数,k表示映射的次数。字节阮bk(u)用到第(k+1)次映射中。
不同于面包师变换t,初始点(Xo, Yo)∈M*由一个有限的二进制序列表示:
![]()
其中:
![]()
![]()
T*等价于s*上的推移算子Φ*:
![]()
其中s*上的替代运算实际上是用:
![]()
代替Xk+1的最低有效位,这里YKLSB是Yk的最低有效位。(这个例子中Yk-1是最低有效位)。
二进制截断面包师变换也是可逆的,并且有:
(3)当0≤Yk< 2l-1时,
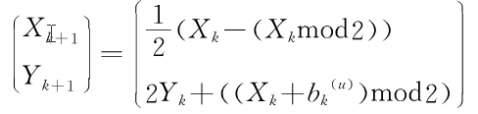
(4)当2l-1≤Yk<2l时,
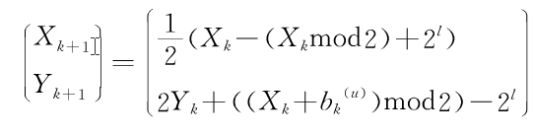
二、三进制下的面包师变换
三进制面包师变换T:M=[0,1)2→M=[o,1)2定义为:
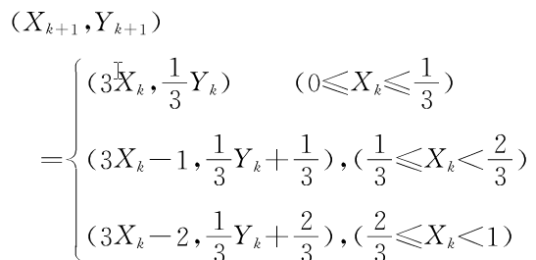
其中(Xk,Yk)表示定义M域中的点(X0,Yo)∈M经过尼次迭代后得到的值。对于任何初始点(Xo ,Yo)∈M,它都可以表示成下列无穷的三进制序列:
![]()
其中:
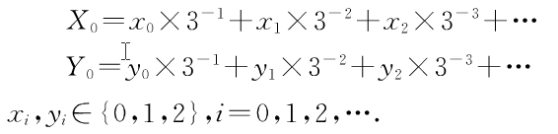
此时T等价于s上的一个推移运算Φ
![]()
显然变换T是可逆的,且它的逆变换T-1为:
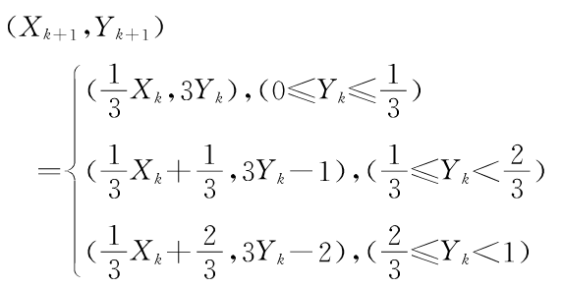
类似于三进制面包师变换,三进制面包师逆变换也等价于一个推移运算Φ-1
![]()
为了把三进制面包师变换应用到数字图象的加密当中,需要考虑离散的三进制面包师变换。
三、基于二进制面包师变换的图象文件加密示例
1、基于位置的图象文件加密

2、基于色彩的图像文件加密

小知识之三进制
三进制是以3为底数的进位制。
曾经被莫斯科大学科研人员用于计算机,在光子计算机研究领域也有涉及。










