基于仿射变换的数字图像置乱加密算法

为了提高图像置乱后的保密性及提高信息隐藏的抗攻击能力，使合法的用户可以更多地自由选择密钥，受可逆线性变换整型化思想的启发，我们提出了一种新的图像加密算法——基于仿射变换的数字图像置乱加密算法。

一、有限整数域上的拟仿射变换

1、整数域上的拟仿射变换

为引入整数域上拟仿射变换的定义，我们先看几何仿射变换的定义。

定义1、仿射变换的一般形式为：

为便于与Arnold变换、排列变换、Fibonacci变换对照，将它写成矩阵的形式：

其中a，b，c，d，e，f为实数．考虑到整数域上的特殊性（x．y，x’，y '）均为整数。通常式（1）我们并不能满足要求，受可逆线性变换整型化思想的启发，我们将根据式（1）构造出一个整数到整数的变换，且满足以下要求：

（1）变换是离散点域{（x，y）：x，y为整数}到其自身的单映射；

（2）变换是离散点域{（x，y）：x，y为整数}到其自身的满映射，即变换是可逆的。

首先介绍整数提升变换的概念．对于变换：

可以构造它所对应的整数变换为：

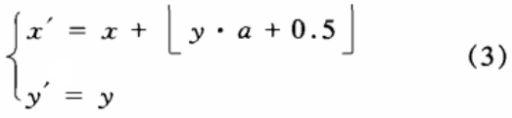
其中[x]表示x的整数部分，加入0.5以实现舍人，从式(3)可以看出，如果输入x，y为整数，那么经过计算得到的x’，y’也必定为整数，同时，我们可以得到变换式(3)的逆变换式：

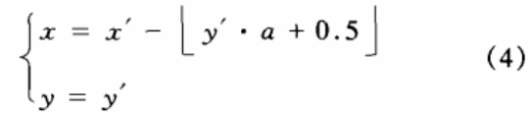
类似地，对于如下变换：

我们可以构造它所对应的整数变换为：

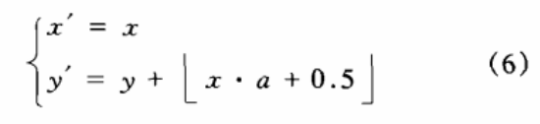
及式(6)的逆变换式：

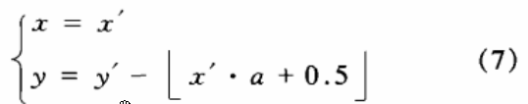
定义2．我们称式(3)，(6)为对应于式(2)．(5)的整数提升变换，式(4)，(7)为式(3)，(6)的逆整数提升变换。

容易看出，整数提升变换的一个突出性质就是可以实现整数到整数的可逆变换．除此之外，整数提升变换的级联也可以实现整数到整数的可逆变换．对于式(1)定义的一般仿射变换，当满足△=时，可将式（1），分解如下：

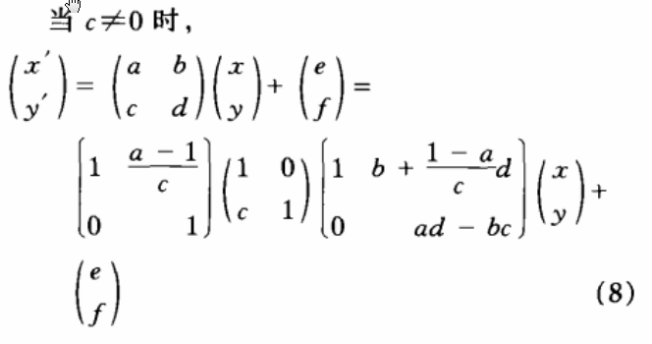
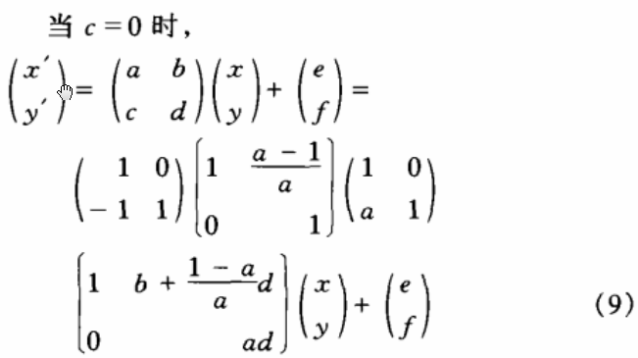
由式(8)，(9)可知，如对e，f简单舍人取整，其他部分以整数提升变换实现，则可以在整数域上实现式(1)所示之仿射变换，注意：当△=-1时，第一次整数提升变换需作适当的修正，即当式(8)中的ad -bc或式(9)中的ad为-1时，式(3)，(4)中第二个等式的右面需加一负号；另外，为了减小舍人误差，可将e，f融人最后一次整数提升变换中进行舍人运算。

值得指出的是，由于在各级整数提升变换中引入了非线性的舍入运算，使得最后得到的结果不再是传统意义上的仿射变换，对此我们引入如下定义：

定义3、对于式（1）定义的仿射变换，如果满足，当x，y∈x时，将整数提升变换实现的形式上的仿射变换称为整数域上的拟仿射变换，简称整数拟仿射变换，整数拟仿射变换有如下4条性质：

性质1、整数拟仿射变换的逆变换一定存在；

性质2、整数拟仿射变换的和不一定是整数拟仿射变换；

性质3、整数拟仿射变换的积仍然是整数拟仿射变换；

性质4、整数拟仿射变换是整数域上的一一变换。

在实际应用中，通常对x，y及x'，y’的取值范围有一定的限制，如限定0≤x，x’<M，0≤y，y'<N，下面介绍有限整数域上的拟仿射变换的概念及构造方法。

2、有限整数域上的拟仿射变换

定义4、有限整数域上的拟仿射变换( Quasi-Affine Transformation on Limited Integer Grids,QATLIG)，它首先是一个变换，满足：

条件1、变换是离散点域{(x，y)：0≤x<M，0≤y<N }到其自身的单映射；

条件2、变换是离散点域{(x，y)：0≤x<M，0≤y<N}到其自身的满映射。

其次，它是式(1)在有限整数域上的一个实现，即可由式(1)改造而来，显然，QATLIG和整数仿射变换有着密切的联系，我们首先介绍有限整数域上的提升变换，在此基础上给出QATLIG的构造方法。

对于式(2)，(5)之线性变换，当限定0≤x<M，0≤y<N时，可以构造相应的有限整数域上的提升变换如下：

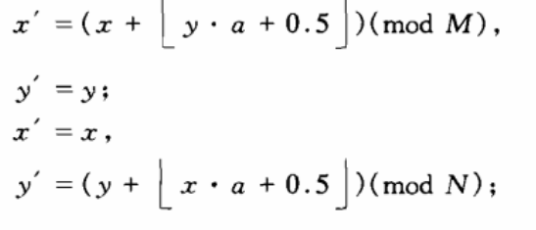
对应的逆变换为：

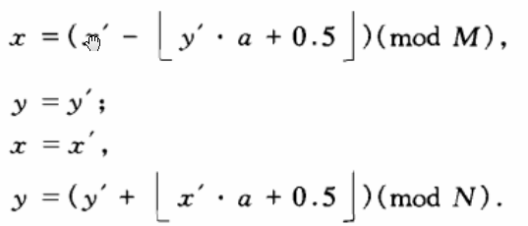
容易看出，有限整数域上的提升变换的一个突出性质就是可以实现有限整数域到有限整数域的可逆变换．除此之外，有限整数域上的提升变换的级联也可以实现有限整数域到有限整数域的可逆变换，对于式(1)定义的一般仿射变换，当满足时，由式(8)，(9)可知，如最后一步作如下变换：

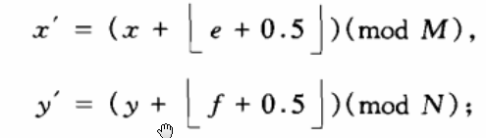
其相应的逆变换为：

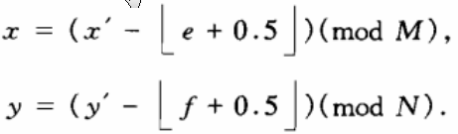
其他部分以有限整数域上的提升变换实现，则可以在有限整数域上实现式(1)所示之仿射变换。另外，为了减小舍入误差，可将e，f融入最后一次有限整数提升变换中进行舍入及取模运算，根据QATLIG的定义及其构造方法，不难得到如下4条性质：

性质5、QATLIG的逆变换一定存在。

性质6、QATLIG的和不一定是QATLIG。

性质7、QATLIG的积仍然是QATLIG。

性质8、QATLIG是有限整数域上的一一变换。

二、 QATLIG在图像置乱中的应用

一幅数字图像可用矩阵A={a(i，j)}N×M表示，其中a(i，j)表示图像在第f行第歹列像素处的灰度值（或RGB分量值）。

数字图像的置乱原理是：将原来点(x，y)处像素对应的灰度值或RGB颜色值移动到变换后的点(x’，y')处。如果对一幅数字图像迭代地使用QATLIG，即将式(2)左端的（x’，y’）T作为下一次相应变换的输入，则可重复这个过程一直做下去。

用第2节给出的QATLIG，随机地选择其变换系数（本例中，a= 9.4849113758545604e+002，b=13322919891824768e+004,c=5.7813914782433339e+∞8.d=8.12(J79454L5277645e+004,P=1.615675,5002857162e
+002,f=2.2755882099826667e+∞B)，对Airplane图像(256×256像素)进行置乱的效果如图1所示。

从图1可以看出，QATLIG用于图像置乱有较好的置乱效果，在经过2次迭代置乱变换后，可将原图像的各种灰度值均匀地分布到图像区域中，从而能较好地隐蔽原图像的信息，为进一步进行图像隐藏打下了良好的基础．而对于其他形式的变换，如Arnold变换，要达到如此的置乱效果，至少要迭代10次以上。

三、QATLIG应用于图像置乱的周期性

对数字图像A={a(i，j)}N×N，某一置乱变换关于A的周期T是指使得图像A经一系列变换后回复到A的最小次数。

显然，上述定义除与具体A的大小有关外，还与A的具体内容有关，它并不能完全刻画出QATLIG的置乱性能，为此引入如下定义。

定义5、对大小为N×M的数字图像A，我们说QATLIG(a．b，c，d，e，f)关于N×M的周期为T，是指当A的任意两个像素没有相同的颜色值时，使得图像A经重复同一变换后又回复到A的最小变换次数为T。

下面以第3节实验中所给出的变换参数定义的QATLIG为例，假定图像为N×N像素，按定义5求得其周期TNo及Arnold变换的周期TNA如表1所示。

在第3节中已经指出，从数据文件加密的角度看，QATLIG优于Arnold变换等几何变换。另一方面，从信息隐藏的角度考虑，图像置乱变换作为进一步操作的预处理过程，比如置乱后再进行隐藏，Arnold变换在进行迭代置乱时，很多时候有较强的纹理特征，在用Cox的水印方法进行隐藏时，为达到隐藏的目的就必须减小其强度控制参数，但这样降低了隐蔽倍道的容量。而QATLIG具有这样的特点：容易构造出好的QATLIG(如第3节实验中所给出的变换参数)，使得图像置乱后，其各种灰度值均匀分布在图像所在的区域({(x，y)：0≤x<M，0≤y<N且为整数}），减少了置乱图像的纹理特征，从而可以增加隐蔽信道的容量。从信息隐藏的角度考虑，QATLIG也优于Arnold等几何变换。

四、基于仿射变换的数字图像置乱加密算法优点

（1）能适用于任意大小的图像，有较大的适用性。

（2）6个变换参数中的5个可以选用随机数，另外一个由约束确定．这大大方便了密钥的选择，增加了系统的安全性。

（3）置乱加密算法可以公开，秘密全寓于密钥中，满足密码学中的Kerckhoffs假设。对于其他固定参数的置乱算法，密钥只能存在于置乱次数中，但由于图像置乱固有的周期性，因此单靠置乱次数作为密钥是十分不安全的。

admin普通用户

海报分享