图像文件加密主要包含两种技术,一种是位置置乱技术,即改变图像的相互位置关系,降低图像的相关性,从而达到图像文件加密的目的。另一种是像素值替代技术,即改变图像每个像素点的像素值,降低图像相邻像素之间的相关性,从而更好地保护图像数据。这两种方法或多或少的都存在有一些缺陷,为此,我们在研究m序列产生原理的基础上,提出了基于置乱和m序列整数调制的图像加密算法。这种方法可以有效地紊乱图像,而且还具有很好的安全性。
一、正弦混沌映射
正弦映射是一个非线性动力系统,其方程为:
![]()
其中μ为正弦映射的系统参数(0<μ≤1),其取值大小决定正弦映射的周期、分岔与混沌三种状态;而xn∈[-1,0)或者xn∈(0,1]。通常采用Lyapunov指数和功率谱两种方法来研究正弦映射的混沌行为。
1、Lyapunov指数法
对一维动力系统xn+1=f(xn),其Lyapunov指数定义为:
![]()
因此,正弦映射量xn+1=μsin( πxn)的Lyapunov指数为:
![]()
当λ>O时,正弦映射处于混沌状态,且此时对初始值敏感;当λ<O时,正弦映射处于周期状态,且对初始值不敏感,而λ=O为临界状态。Lyapunov指数大于零是判断非线性系统混沌行为的一个必要条件,但不是充分条件。
2、功率谱方法
对于时间序列x1,x2,…,xN,其功率谱可以通过以下步骤进行计算:
1)先对N个采样值加上周期条件知Xn+j=Xj,计算自相关函数:
![]()
2)然后对Cj进行离散傅立叶变换,得到傅立叶系数:
![]()
记ak=Re( Pk),bk=Im( Pk),则有Qk=ak2+bk2。这里称Qk为功率谱或者功率谱密度函数。
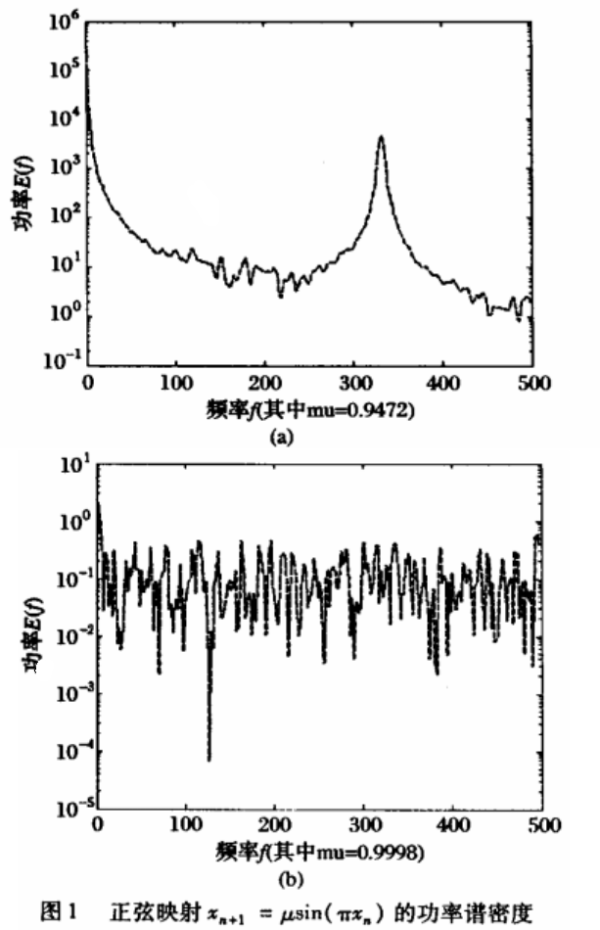
图1为正弦映射在不同系统参数下产生序列的功率谱,从功率谱进行分析可以观察到典型的混沌特性。当功率谱图具有单峰(或多峰),则对应于周期(或拟周期)序列,如图1(a)所示。可以验证,当时,正弦映射的Lyapunov指数大于零,但其功率谱为单峰,此时由正弦混沌系统产生的序列不是混沌序列。当功率谱图无明显的峰值或峰值连成一片,则对应混沌序列,如图1(b)所示o以上表明,取定一个大于零的系统参数p后,可以进一步计算序列的功率谱,由此确定序列是否为混沌序列。
二、m序列变换与m序列整数调制
1、m序列原理
伪随机序列可以通过一个n级线性反馈移位寄存器得到,如图2所示。
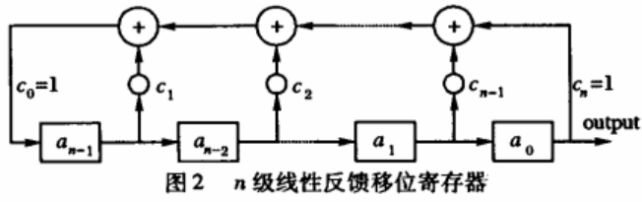
图中an-1,an-2,…,a1,ao为寄存器的状态,反馈线的连接状态用ci表示。ci =1表示反馈线接通(参与反馈),ci=O表示反馈线断开,但是cn= co=1。寄存器的每一级输出经反馈
相加后作为最高位的输人an,n级线性反馈移位寄存器可能产生的最长周期为2n-1,称这种最长的序列为m序列。线性反馈移位寄存器能产生m序列的充要条件是反馈移位寄存器的特征多项式为本原多项式。
2、m序列变换
根据m序列的理论,本文设计了一种新的图像位置置乱方法,即称之为m序列变换,其变换原理如下:
设数字图像为f(x,y),x=0,1,…,m-1;y=0,1,…,n-1,若m和m满足2kx-1<m<2kx和2ky-1<n<2ky,取一个k=kx+ky级线性反馈移存器的本原多项式f(x)作为其特征方程,且移位寄存器的初始状态为非零状态。则数字图像f(x,y)的水平坐标≈和垂直坐标儿可分别用前kx和后ky个移位寄存器的状态来表示,其对应关系如下式:
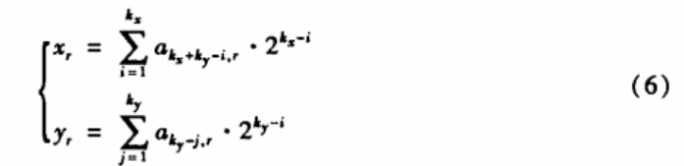
其中r表示m序列由第0时刻开始的移位次数,r∈{0,1,2,…,2k-2}。而akx+ky-i,r和aky-j,r分别表示前kx个和后ky个移位寄存器移位r次的状态。
当然,可任取kx个移位寄存器的状态按照不同的排列方式得到xr,剩余的ky个移位寄存器的状态也按照不同的排列方式得到Yr,这等效于将移位寄存器的状态{a0r,a1r,…,akx+ky-i,r}进行排列,为了描述方便,排列后的移位寄存器状态用{b0r,b1r,…,bkx+ky-i,r}表示,则(6)式可改为:
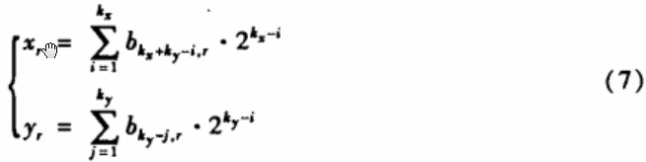
根据m序列原理可知xr∈{0,1 ,…,2kx-1}和yr∈{0,1,….2ky-1},但xr和yr不能同时为零。在图像位置量乱中,x和y可作为原图像经过m序列变换后的水平和垂直坐标。显然,只有当m=2kx和n= 2ky时.m序列在移位时得到的‘和y,不可能超出图像的尺寸界限;否则,由(7)计算得到的毛和儿就有一部分数据超出了图像的尺寸界限,在m序列变换中对这些点要作舍弃处理。因此,m序列变换算法描述如下:
(1)任意选择表示图像位置xr与yr时使用的移位寄存器的一种排列方式,并任意选择(x’o,y'o),将f(x,y)第1个像素点(0.0)的值与f(x,y)中任意一个像素点(x’o.y'o)的值相互交换,x’o和,y’o分别对应移位寄存器经排列后前kx个和后ky食的状态,其对应关系参照式(7)。其中x’o =0,1,2,…,m- 1;y'o=0,1,2,…,n-1,但x’o和Y'o不能同时取零。
(2)m序列移位一次,并由移位寄存器状态用式(7)计算x1和y1,检查x1和y是否满足式(8):
![]()
若不满足,m序列继续移位,并由移位寄存器状态用式(7)计算x2和y2,检查x2和y2是否满足式(8),直到寻找到满足式(8)的xr和yr为止,并把此时的xr和yr记为写x1'和y1',将f(x,y)第2个点的像素值f(x,y)与(x’1.y'1)中点的像素值相互交换。
(3)m序列继续移位,按照步骤(2)方法对f(x,y)其他像素点与对应点的像素值相互交换,m序列经过一个周期(t=2k-1)后,正好将f(x,y)除(M -1,N一1)一点外的其他所有像素点与对应点的像素值相互交换了一遍。
(4)最后,m序列继续移位,按照步骤(2)方法,此时找到满足式(8)条件的点为(x'o,y'o)点,将(x,y)的点(M -1,N一1)与点(x’o,y'o)的像素值相互交换。
上述过程实现了图像的m序列变换。当特征方程f(x)为本原多项式时,k=kx+ky级线性反馈移位寄存器的周期为2kx+ky一1,舍弃不同时满足0≤xr≤M-1和0≤yr≤N-1的点,用它即可实现图像的位置置乱。其图像置乱的结果取决于任意选择的移位寄存器的排列方式和任意选择的(x’o,y'o),它们均可作为可作为图像加解密的独立密钥。其中k=kx+ ky个移位寄存器的捧列方式为k!,而x’o和y'o的密钥空间分别是x’o∈{ 0,1,…,m-1}和y'o∈{0,1,…,n-1},但是x’o和y'o不能同时为零。所以,m序列变换的总密钥空间大小为K!(MN-1)。
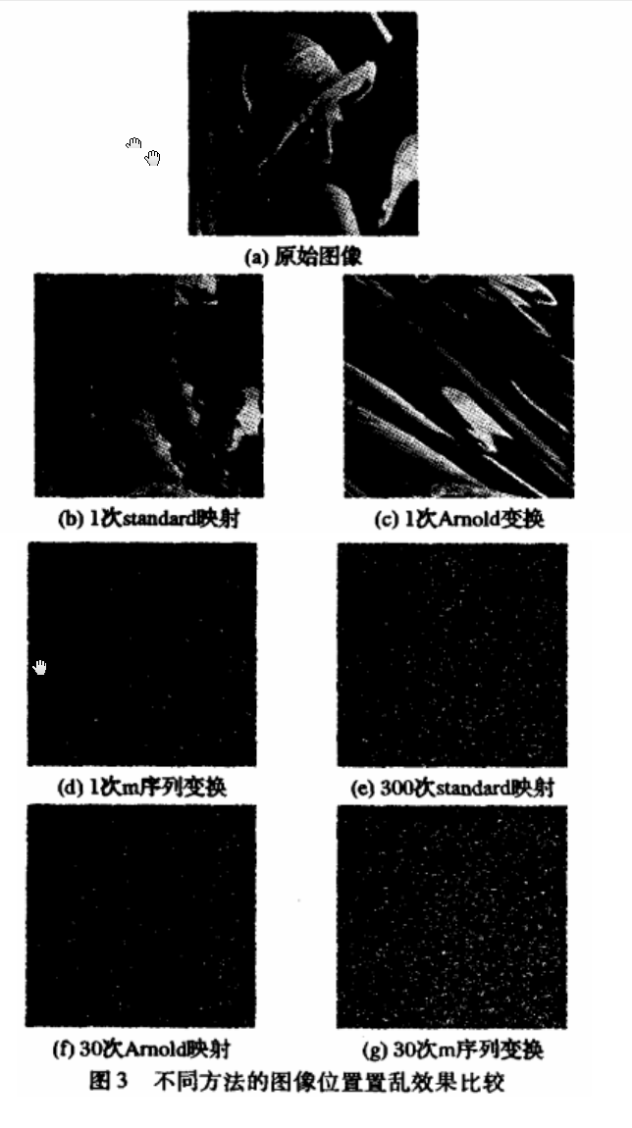
图3是分别采用m序列变换和其他方法对一幅256×256的lenna灰度图像加密的实验结果。
从以上实验结果可以看出,常用的一些位置置乱变换,如8tarid8td映射和Amold变换均需要变换多次后才能达到较好的图像置乱效果,而m序列变换只需变换一次就可以达到非常好的置乱效果,说明本文提出的m序列变换对图像进行位置置乱时其加密效率高。原因在于这种方法是依次不断地交换两个像素点的位置并利用了m序列的伪随机特性,加密过程为非线性过程。因此,它不仅图像文件加密效果好,而且加密效率高。
3、 m序列整救调钥
设f(x,y),x=0,1,…,M- 1;y=0,1,…,N-1为一幅待加密灰度图像,灰度级为L∈ {0,1,2,…,255},用正弦映射产生一幅同样尺寸大小的混沌图像,用g0(x,y),x∈{0,1,
…,m-1},y∈{0,1.…,n- 1 }表示,其灰度级为f’={ 1,2,…,255}。根据f(x,y)和g0(x,y)的灰度级范围,可以取一个本原多项式f(x)=x8+x4+x3+x2+1作为n=8级的m序列产生器的特征方程。依据m序列原理可知,m序列的周期为p=2n-1=255,即m序列产生器中移位寄存器有255种状态(均为非零状态),若用它们表示混沌图像go(x,y)的灰度值,二者正好一一对应,其对应关系如下:
![]()
其中g0(x,y)表示(x,y)处的混沌图像g 0(x,y)的灰度值。
因此,图像的m序列整数调制方法可描述如下:
(1)待加密图像f(x,y)在(x,y)处的像素值为f(x,y)≠0,以f(x,y)像素值作为g0(x,y)在(x,y)处像素go(x,y)的m序列移位次数,go(x,y)对应m序列产生器中移位寄
存器的一个初始状态vo={a70,a60,a50,a40,a30,a20,a10},经过f(x ,y)次移位后,移位寄存器的状态发生改变,其状态变为vm={a7m,a6m,a5m,a4m,a3m,a2m,a1m},此时v状态可对应一个整数gm(x,y),对应关系为;
![]()
(2)若待加密图像f(x,y)在(x,y)处的像素值以f(x,y)=0,g(x,y)= 0。
对所有像素点作上述处理后,得到的所有gm(x,y)构成一个矩阵gm(x,y),它即为m序列整数调制后的加密图像。
4、m序列整数调整的快速算法
从m序列整数调翩原理可以看出,采用m序列整数调制进行图像加密的计算复杂度高,整个加密过程所需要的时间很长,其原因是当f(x,y)的像东值不为零(尤其是较大)时,m序列整数调钥的移位次数也相应增多,造成总的运算复杂度增加。为此,本文设计了一个快速算法:
算法思想:考虑到用m序列整效调制进行图像文件加密实际上包括很多重复运算,可以把g0(x,y)经f(x,y)≠o次m序列移位后得到gm(x,y)设计成一个映射表(也称为映射关系>o并将该映射表保存为一幅灰度图像( en. bmp),其灰度级为{ 1,2,…,255}。此外,用m序列整数调制进行图像解密的计算复杂度也很高,类似用m序列整数调制进行图像加密的方法把由gm(x,y)≠0和go(x,y)得到f(x,y)≠0也设计成另一个映射表,并保存为另一幅灰度图像( de. bmp)。
这样,对图像f(x,y)进行加密时,当f(x,y)≠0时,只要从映射表( en. bmp)中寻找对应关系就可明显的提高图像加密的速度。同理,当gm(x,y)≠0。图像解密时也是在映射表( de.bmp)中寻找对应关系。
三、 图像混沌加密算法
第1步 输入原始图像,用矩阵表示为fo(x,y),X∈{0,1,…,M-1},y∈{1 0,1.…,N-1},灰度级L=256。
第2步 对fo(x,y)进行图像预处理:
![]()
其中g 1(x,y)和g2(x,y)是由(1)式正弦混沌系统迭代并作取整得到的两幅混沌图像。可使图像经此预处理后f1(x,y)接近于随机图像。
当原图像中含有大量的零并且比较集中或有规律时,若不作上述顶处理而直接进行m序列整数调制,其图像加密效果不理想。因此,上述采用改进的猫映射进行图像预处理的目的是使m序列整数调制方法适合于任意图像文件加密。
第3步用3节和4节的m序列整数调制及其快速算法,将f1(x,y)图像调制在混沌图go(x,y)上,得到加密图go(x,y)。
第4步用2节m序列变换对gm(x,y)进行图像的位置置乱,得到f2(x,y)。
解密算法是加密算法的逆过程。
四、基于置乱和m序列整数调制的图像加密算法优势
与其他加密算法相比,本文加密算法具有以下优点:
(1)m序列变换是利用交换图像像素点的值,无须证明m序列变换是否为一一映射,采用m序列变换肯定保留了原图像的所有信息。其加密效果好,效率高,具有很好的保密性,密钥空间由任意选择的移位寄存器的捧列方式和任意选择的(x'0,y'o)决定。m序列变换的总密钥空间大小为K(MN-1)。
(2)m序列整数调制与按位异或运算用于图像文件加密相比,它更难解密。按位异或运算对图像是一种伪装,如果揭开这层面纱,一切暴露无遗;而m序列整数调制是将待加密目像作为m序列整数调制的调制参数,将待加密图像信息调制在一幅混沌图像上,要解密它必须准确知道密钥x0和μo。
(3)该加密算法对图像尺寸大小没有限制。
(4)该加密算法总的密钥空间非常大。
小知识之M序列
M序列(即De Bruijn序列)又叫做伪随机序列、伪噪声(PN)码或伪随机码。可以预先确定并且可以重复实现的序列称为确定序列;既不能预先确定又不能重复实现的序列称随机序列;不能预先确定但可以重复产生的序列称伪随机序列。











