随着互联网和多媒体技术的广泛使用,迫切需要快速而安全的图像加密算法保证涉密图像信息的保存与传输。为了应对这种挑战,研究人员已提出了大量的图像加密算法。基于复合离散混沌系统的图像加密算法就是其中应用比较广泛的一种,接下来我们就简单的给大家做一下介绍。
一、复合离散混沌系统
1、复合离散混沌系统的定义
定义设2个离散混沌系统f(),g():xn+1=f(xn,pf),yn+1=g(yn,pg),定义一个新的离散混沌系统φ()如下:
![]()
其中,Q是大于0的自然数;(Xmin,Xmax)的典型取值区间是(0.2,0.8);yn+1是由g()产生的混沌序列,其值通常也要求在(0.2,0.8)之间;△是f()的迭代次数修正量,如果fN(yn+1-xmin)/(xmax-xmin)(xn)∈(Xmin,Xmax),则△=O,否则,继续迭代fN(yn+1-xmin)/(xmax-xmin)(xn),直到其值介于区间(Xmin,Xmax)内,则△就等于继续迭代的次数。
2、混沌序列的生成
根据上节的描述,本文选择Logistic映射作为φ()中的f(),帐篷映射作为φ()中的g(),构成改进的离散混沌系统φ()。Logistic映射和帐篷映射分别定义如下:
![]()
标准帐篷映射的方程为:
![]()
则产生混沌序列过程如下:
(1)选定2个初始参数i和j,分别作为Logistic映射和帐篷映射的初始值,同时确定式(2)中的Q值,i,j,Q即为此加密算法密钥。
(2)利用式(4)和j产生混沌序列y1,y2,…,yn。
(3)利用式(1)得到φ()的混沌序列x1,x2,…,xn。
(4)利用下式将该序列离散化得到混沌序列φ(1),φ(2),…,φ(k),…,φ(n):
![]()
其中,N是图像的颜色深度(对于256级的灰度图像,N=256);(Xmin,Xmax)的典型取值区间是(0.2,0.8)。
二、基于复合离散混沌系统的图像置乱加密算法
对于一个数字灰度图像I,其大小为M×N,利用复合离散混沌系统φ()来产生混沌实值序列,然后通过下面描述的置乱加密算法即可对图像,逐行进行置乱和解密。
1、置乱加密算法
置乱加密算法步骤如下:
(1)经复合离散混沌系统得到混沌实值序列φ(1),φ(2),…,φ(k),…,φ(n)。
(2)通过排序变换,将实值序列集合{φ(1),φ(2),…,φ(k),…,φ(n)}中的n个值由小到大排序,形成有序序列φ1,φ2,…,φn。
(3)确定混沌实值序列{φ(1),φ(2),…,φ(n)}中的每个φ(i)在有序序列{φ1,φ2,…,φn}中的位置编号,形成置换地址集合T={ t1,t2,…,tn}。
(4)按置换地址集合{ t1,t2,…,tn}对图像的第1行像素进行置换,同时将其第i列像素置换至第ti列,i=1,2,…,n。
(5)置φ(1)=φ(n),对2~M行,重复步骤(2)-步骤(5)。
2、解密算法
可采用类似置乱的步骤,即只需将步骤(4)改为:按置换地址集合{ t1,t2,…,tn}对图像的第1行像素进行置换,同时将其第ti列像素置换至第i列(i=1,2.…,n)即可实现图像的解密。
三、实验仿真
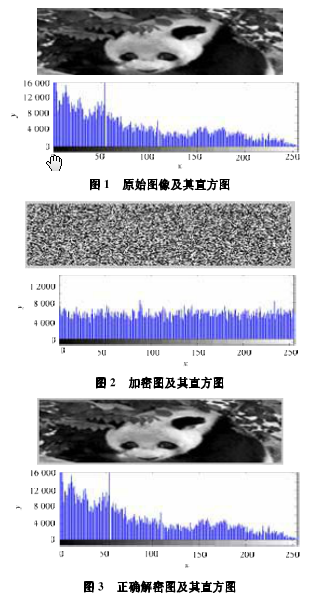
选择大小为220×60的灰度图像(如图1所示)作为实验对象,利用Matlab 7.0编程实现本加密算法。选取密钥i=0.666 66,j=0.555 55,Q=2,为了增强生成混沌序列的安全性,除去序列的初始段,然后进行加密运算产生加密图像如图2所示),正确解密后的图像如图3所示。
四、加密算法的安全性分析
一个好的加密算法应该能够抵抗各种密码分析攻击,并且其安全性不应该依赖于加密体制或算法的保密。针对本文提出的加密方案进行的各种安全性分析如下。
1、置乱度分析
置乱度(SM)来评估加密图像的像素置乱程度,它的计算式为:

其中,![]() 表示原始图像;
表示原始图像;![]() 表示置乱后图像;
表示置乱后图像;![]() 表示与原始图像大小相同的标准置乱图像。
表示与原始图像大小相同的标准置乱图像。
在本加密算法中,将尺定义为均匀噪声图像,均匀噪声具备良好的随机性和混乱性,可以作为衡量像素置乱度的标准。利用实验结果多次计算SM得到平均值为:SM=0.887。
可见,给图像文件加密的像素置乱度与均匀噪声相近,具有良好的置乱性。
2、抗攻击测试
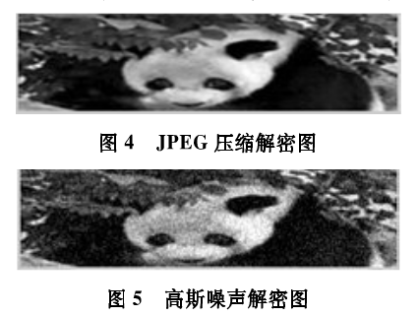
图4是加密图像经JPEG压缩为原大小20%后的解密图像,图5是加密图像受到10%强度的高斯噪声干扰后的解密图像。可以看出解密图像效果较好,具有较强的抗攻击能力。
本文的加密算法具有良好的密钥敏感性和很大的密钥空间,同时具有较好的抗统计攻击、差分攻击和选择明文攻击能力。另外,由于排序变换的强不规则性,还增加了加密算法对混沌映射初始值的敏感度和置乱的复杂度,从而使得新的混沌图像置乱加密算法具有较高的安全保密性能和足够大的密钥量。
小知识之离散
所谓离散(Measures of Dispersion),即观测变量各个取值之间的差异程度。它是用以衡量风险大小的指标。










