Rijndael加密算法如何在ARM微处理器上实现

Rijndael加密算法以安全性好、运算速度快、存储要求低、灵活性强，为计算机网络和电子商务的发展提供了强有力的保障。而ARM微处理器凭借强大的处理能力和极低的功耗，被越来越多的企业来使用。那么我们今天就来讲一下Rijndael加密算法是如何在ARM微处理器上实现的。

一、Rijndael加密算法简介

1、Rijndael加密算法流程结构

Rijndael加密算法的128位输入分组用以字节为单位的正方形矩阵描述。该数组被复制到State数组。加密过程分为四个阶段：密钥扩展、轮密钥加、Nr—1（对应128、192、256位密钥长度，Nr分别为10、12、14）轮变换及最后一轮变换。轮变换包括字节代换、行移位、列混淆和轮密钥加四个过程，最后一轮变换包括字节代换、行移位和轮密钥加三个过程。用伪C代码表示如下：

Rijndael(State,CipherKey)

{

KeyExpansion(CipherKey,ExpandKey);

//密钥扩展AddRoundKey(State,RoundKey);

//轮密钥加For(i=1;i<Nr;i++)

Round(State,ExpandKey+4*i);

//轮变换

FinalRound(State,ExpandKey+4*Nr);

//最后一轮变换

}

Round(State,RoundKey)

{

//轮变换SubByte(State);

//字节代换ShiftRow(State);

//行移位MixColumn(State);

//列混淆AddRoundKey(State,RoundKey);

//轮密钥加

FinalRound(State,RoundKey)

{

//最后一轮变换

SubByte(State);ShiftRow(State);

AddRoundKey(State,RoundKey);

}

2、Rijndael加密算法所使用的主要变换

（1）字节代换SubByte

用一个简单的查表操作代替了基于矩阵乘法的复杂仿射变换。Rijndael定义了一个16_16字节的S盒矩阵,包含8位值所能表达的256种可能的变换。把State中每个字节的高4位作为行值,低4位作为列值,取出S盒中对应行列的元素作为新的字节输出。

行移位变换ShiftRow:State的第一行保持不变，第2、3、4行分别循环左移1、2、3个字节。

（2）列混淆变换MixColumn

可表示为如下基于系数矩阵CoefMix与State的矩阵乘法：

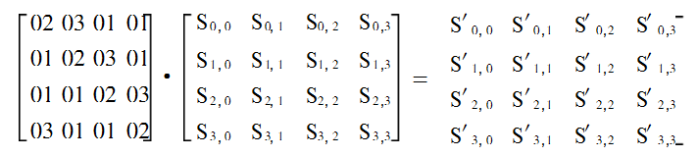
乘积矩阵中的每个元素S’i,j是系数矩阵中一行元素CoefMix[i,k]与State矩阵中对应一列元素State[k,j]的乘积之和。这里的加法与乘法都定义在有限域GF(28)上：加法即按位异或操作，乘法遵循GF(28)上的多项式乘法规则。

（3）密钥扩展KeyExpanxsion

以4个字密钥为输入，生成44字扩展密钥数组w[44]，为初始轮密钥加阶段和后面10轮变换提供轮密钥。输入密钥直接被复制到扩展密钥数组的前4个字，然后每次用4个字填充扩展密钥数组余下的部分。在扩展密钥数组中，w[i]值依赖于w[i-1]和w[i-4]。w数组中下标不是4的倍数时，w[i]为w[i-1]和w[i-4]的异或。下标为4的倍数时，首先将w[i-1]的4个字节循环左移1个字节，然后利用S盒对每个字节进行字节代换，再与轮常量按位异或。轮常量是1个字，其最右边3个字节为0，最左边1个字节的值RC[j]与轮数j相关。RC[1]=1，RC[j]=2#RC[j-1]，乘法定义在GF(28)上。RC[j]值以十六进制表示。

（4）轮密钥加AddRoundKey

轮密钥加AddRoundKey是基于State列的操作，即把State一列中的4个字节与轮密钥RoundKey的1个字进行异或。

二、Rijndael加密算法如何在ARM微处理器上实现

1、源程序组成及功能

源程序包含main.c和ARM汇编程序Rijndael.s。main.c用C语言编写，主要完成调用，C/OSII函数进行系统初始化及I/O的全部功能，并调用Rijndael.s对明文加密。明文、密钥及密文均在开发板显示屏上输出。

Rijndael.s用ARM汇编编程语言编写,是实现加密算法的关键程序。

2、Rijndael.s程序实现加密算法步骤

Rijndael.s主要通过ARM汇编子程序调用完成加密算法，包括1个代码段和1个数据段。它把算法所使用的所有变换均用同名ARM汇编子程序实现。代码段包括以下几个模块:

首先，进行明文、密钥预处理。明文可以从开发板键盘上接收，也可以是常量或参数传递过来的变量。

其次，调用子程序KeyExpansion完成密钥扩展。

第三，调用子程序AddRoundKey完成初始轮密钥加。

第四，轮变换。

包括四个步骤：a、调用子程序SubByte进行字节代换；

b、调用子程序ShiftRow进行行移位；

c、调用子程序MixColumn进行列混淆；

d、调用子程序Ad__dRoundKey进行轮密钥加。本过程重复9次。

第五，最后一轮变换。

包括三个步骤：

a、调用子程序SubByte进行字节代换；

b、调用子程序ShiftRow进行行移位；

c、调用子程序AddRoundKey进行轮密钥加。

最后，对生成的密文进行进一步处理，即把密文视为4_4数组，将其行与列对调。

在数据段中对转换过程中使用到的部分数据或中间变量进行了定义并初始化。如字节代换中的S盒及列混淆变换中的系数矩阵等。

3、ARM汇编子程序代码设计举例

在所有子程序中，列混淆变换和密钥扩展的代码设计难度较高，算法较复杂。下面是列混淆子程序的代码设计：

MixColumn;子程序入口

ldrr0,=State;取变量地址

ldrr1,=CoefMixldrr2,=Temp;Temp中间变量

movr3,#0;i=0

loop_i;i循环入口

movr4,#0;j=0loop_j;j循环入口

movr5,#0;k=0loop_k;k循环入口

movr6,r3,lsl#2

addr6,r6,r5

ldrbr6,[r1,r6];读取CoefMix[i,k]

movr7,r5,lsl#2

addr7,r7,r4

ldrbr7,[r0,r7];读取State[k,j]

loop_temp;此循环用来计算

movr8,r3,lsl#2

addr8,r8,r4

andr9,r6,#1

cmpr9,#1;判断CoefMix[i,k]的最低位是否为1

bnenotequal;若不为1,转向执行

ldrbr9,[r2,r8];若为1,则Temp[i,j]+=State[k,j]

eorr9,r9,r7strbr9,[r2,r8]

notequal

movr6,r6,lsr#1;CoefMix[i,k]逻辑右移1位

andr9,r7,#0x80

movr7,r7,lsl#1;State[k,j]逻辑左移1位

andr7,r7,#0xff

cmpr9,#0x80;移位后State[k,j]最高位是否为1

bltlittlethan;如不为1,转向执行

eorr7,r7,#0x1b;如为1,则State[k,j]与#0x1b异或littlethan

cmpr6,#0;CoefMix[i,k]与0比较

bgtloop_temp;如大于0,转到标号loop_temp处执;行,否则读取CoefMix[i,k+1]

addr5,r5,#1cmpr5,#4blt

loop_k

;执行k循环

addr4,r4,#1cmpr4,#4blt

loop_j

;执行j循环

addr3,r3,#1cmpr3,#4bltloop_I;执行i循环

movr3,#0renew

;用Temp更新Stateldrbr4,[r2,r3]strbr4,[r0,r3]addr3,r3,#1cmpr3,#16bltrenewMixColumnend

movpc,lr

;子程序返回

三、Rijndael加密算法实现效率比较

在调用ARM汇编程序实现Rijndael加密算法之余，还在嵌入式微处理器ARM上通过调用C子程序实现了Rijndael算法，同样获得了正确结果。表1、表2是两种实现方式的空间与时间效率比较。

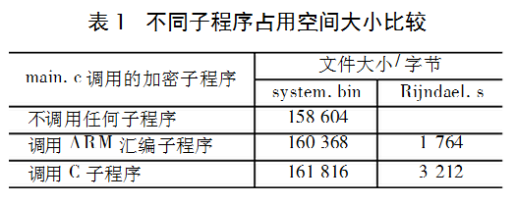
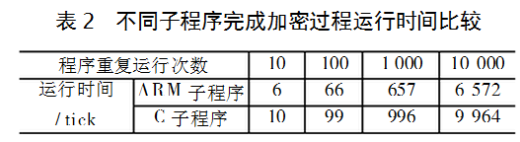
由表1知，ARM子程序比C子程序所占用空间明显小得多，前者仅为后者的55%。由表2,运行一次ARM汇编程序Rijndael.s程序完成加密算法，仅需约0.657tick(此处，1000tick=1s)，而运行一次C子程序约需0.996tick，比前者增加了52%。

Rijndael加密算法在嵌入式微处理器ARM上的实现具有一定的实用价值。经UniversityofCalifor nia，SanDiego在因特网上提供的测试程序InteractiveRi jndaelTestVectorsinJavaScript验证，本实现加密算法是正确的。

admin普通用户

海报分享