目前加密技术绝大部分只是对数字图像的像素位置进行混沌加密,即只是对数字图像的像素位置进行置换,而像素值却保持不变,这些导致这些加密技术存在一些安全隐患,如图像的直方图在置换前后仍然一致。为克服这些缺陷,我们使用改变图像像素位置和像素值的思想对数字图像的混沌加密技术进行研究,提出一种基于像素值双重置换与像素位置的混沌加密算法。
一、数字图像像素位置与像素值双重置换的混沌加密
1、混沌图像加密技术
混沌图像加密技术是近年来应用非常普遍的一种数字图像加密技术,混沌现象是指在非线性动态系统中出现的确定性和类似随机的过程,混沌动力学在此基础上得到迅猛发展,这使得混沌可以用来作为一种新的密码体系,可以加密文本、声音及图像数据。1997年Fridrich首次将混沌加密方法应用到图像加密中,随后,混沌图像加密技术成为数字图像加密技术研究的热点。
混沌加密的原理:将原始信息与混沌发生器产生的混沌序列进行特定的运算,使原始信息转换为具有类似随机噪声的性态,从而对数字图像文件加密。解密就是将加密信息与混沌发生器产生的混沌序列进行反运算,去除混沌信号,使原始信息恢复。混沌加密与解密原理如图1所示。
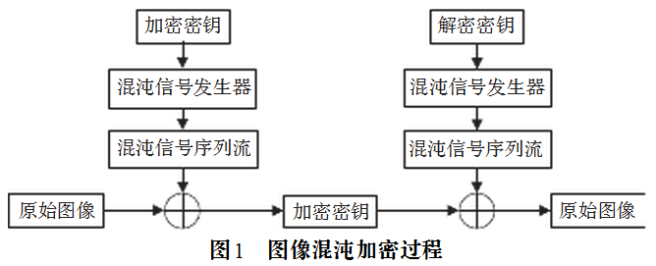
混沌加密技术效率高、操作速度快、实施简易、计算费用低廉,使得基于混沌的图像加密[17]可行性好,在军事、工业以及商业应用的图像和视频通信方面具有广阔前景。然而传统的混沌加密技术只是利用混沌序列与原始信息进行某种运算,使得原始信息变为具有类似随机噪声的性态,从而达到加密目的。目前绝大多数混沌加密算法实质上是单一的图像像素值置乱或图像像素位置置乱,而单一的使用其中任一种都无法保证图像具有较高的安全性,存在一定的安全隐患。
2、数字图像像素位置与像素值双重置换的混沌加密
数字图像通常用二维数组Am×n保存,每个数组元素ai,j的值表示数字图像对应像素的RGB灰度值以及Alpha值,混沌加密技术主要是通过数学变换,即二维矩阵的数学变换,将原数字图像矩阵Am×n置换为二维矩阵Bm×n,使数字图像像素点位置发生变换,从而破坏原数字图像的有序性,达到置乱的目的,从而实现对数字图像加密。但存在一个缺陷,就是无论经过多么复杂的变换,只改变了数字图像像素位置,而数字图像矩阵中的元素即图像像素的灰度值和Alpha值没有改变,因此图像的灰度直方图不会发生变化。攻击者可能通过像素比较的方法加以破解,因而像素位置置乱与像素值置乱相结合成为发展的必然。本文提出的基于数字图像像素位置与像素值双重置换的混沌加密思想就是为此而提出的,其加密思想是:不但对数字图像的像素位置进行置换,而且对其像素值也进行变换,从而改变数字图像的直方图,使安全性进一步提高。具体的加密和解密过程如图2所示:
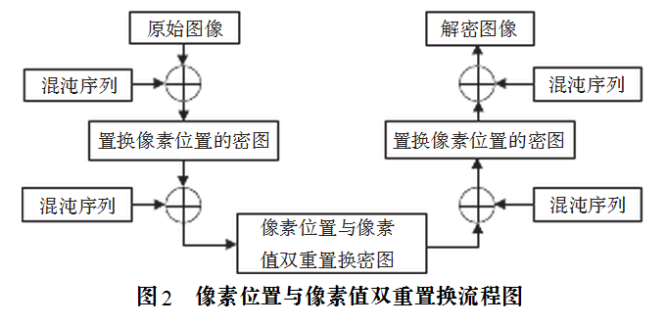
其加密过程具有两个步骤:第一步对数字图像进行像素位置置换,即对像素位置加密;第二步对经过像素位置加密得到的密图再进行像素值的变换,即通过设置加密算法,对密图的每个像素的像素值进行加密,改变密图的R、G、B值,甚至改变Alpha值(透明度),即改变各像素的灰度值。表示数字图像的二维矩阵中对应的每个元素值就表示数字图像对应位置的像素值,一般情况是32位4个字节,具体的存储结构如图3所示:
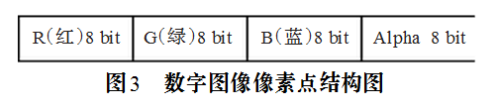
通过加密算法对每个像素的32bit进行置换,即可以改变图像的像素值。这种加密方法弥补了常用的加密技术只置换像素位置的不足,将提高加密算法的抗攻击能力。
二、像素值双重置换与像素位置的混沌加密算法加密算法与解密算法
基于混沌的数字图像像素位置与像素值双重置换的加密过程如图2所示,分两个步骤进行,第一步就是对图像像素位置进行置换,第二步再进行像素值的置换,从而得到密图。在混沌系统中Logistic混沌系统应用非常广泛,而且具有代表性,因此在加密和解密过程中采用的混沌函数是Logistic混沌函数。此系统具有极其复杂的动力学行为,在加密领域的应用十分广泛,其定义如下:
![]()
其中u_(0,4]被称为Logistic参数。研究表明,当X_(0,1)时,Logistic映射处于混沌状态,由初始条件X0在Logistic映射作用下产生的序列是非周期的、不收敛的,而在此范围之外,生成的序列必将收敛于某一个特定的值。
第一步对数字图像像素位置进行置换的算法如下:
(1)将数字图像矩阵Am′n按行扫描形成长度为m′n的一维序列P{P1,P2,......,Pm′n}。
(2)用Logistic混沌函数产生一个长度为m′n的混沌序列L{L1,L2,......,Lm′n},并且将L{L1,L2,......,Lm′n}与P{P1,P2,......,Pm′n}中的元素一一对应。
(3)将所产生的混沌序列L{L1,L2,......,Lm′n}的m′n个值由小到大排序,形成有序序列L'{L'1,L'2,......,L'm′n},由于L{L1,L2,......,Lm′n}与P{P1,P2,.....,Pm′n}中的元素一一对应,P{P1,P2,......,Pm′n}也由同样的置换规则置换成P'{P'1,P'2,......,P'm′n}。
(4)将一维序列P'{P'1,P'2,......,P'm′n}按顺序每m个元素构成一行,从而得到二维矩阵Bm′n,Bm′n就是加密后的图像矩阵。
具体的置换过程如图4所示。
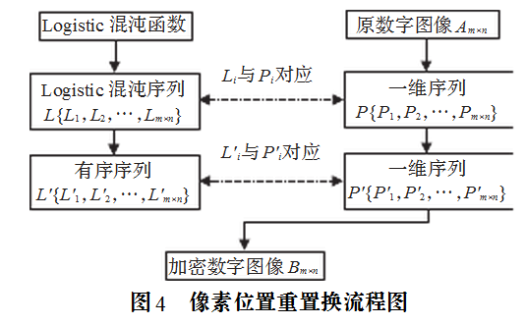
第二步对数字图像像素值进行置换的算法如下:
(1)构造一个长度为256的一维序列C{C0,C1,......,C255},令C0=0,C1=1,…,C255=255。
(2)用Logistic混沌函数产生一个长度为256的混沌序列L{L0,L1,......,L255},并且将序列L{L0,L1,......,L255}与序列C{C0,C1,......,C255}中的元素一一对应。
(3)将所产生的混沌序列L{L0,L1,......,L255}的256个值由小到大排序,形成有序序列L'{L'0,L'1,......,'255},由于L{L0,L1,.....,L255}与序列C{C0,C1,......,C255}中的元素一一对
应,C{C0,C1,......,C255}也由同样的置换规则置换成C'{C'0,C'1,......,C'255}。
(4)将Bm′n中的元素bi,j(表示经过像素位置置换所得加密图像的像素值)的R、G、B、Alpha分量分别进行像素值置换,具体置换规则:
C{C0,C1,......,C255}与C'{C'0,C'1,......,C'255}中的元素是一一对应的,将Bm′n中的元素bi,j进行置换,Bm′n是表示彩色数字图像的矩阵,因此bi,j的R、G、B、Alpha分量的值不同,要对彩色数字图像进行加密,则必须分别对bi,j的R、G、B、Alpha几个分量进行像素值混沌加密。以bi,j的R分量为例,若bi,j的R分量原来为Cr,则将bi,j的R分量转换为C'r,即用C'r置换bi,j的R分量,从而对bi,j的R分量进行了像素值的置换。
(5)重复(4),采用类似的算法对bi,j的G、B、Alpha分量进行像素值的混沌加密,从而对bi,j的R、G、B、Alpha分量分别了进行像素值混沌加密,由此得到数字图像矩阵Cm′n即是经过像素位置与像素值双重混沌加密后的密图。
解密过程也分为两个步骤,与加密过程正好互逆,先将密图Cm′n经过像素值的混沌解密得到经过像素位置混沌加密的密图Bm′n,最后将Bm′n经过像素位置的混沌解密,得到原数字图像Am′n,完成解密。根据加密的算法设计,易得具体的解密算法。
三、加密效果比较
1、加密效果图
为检验算法的加密效果,以图5(a)为原数字图像进行加解密实验。图5(b)为只经过像素位置置换的加密密图,图5(c)为只经过像素值置换的加密密图,图5(d)为经过像素位置与像素值双重置换的加密密图。
由图5可以得出,只经过像素位置混沌加密的密图图5(b)效果比较好,图像像素点分布比较均匀。而只经过像素值置换的加密密图图5(c)仍然具有一些原图像的细节信息,加密效果不是很好。然而经过像素位置与像素值双重置换加密的密图图5(d)的图像像素分布均匀,已经覆盖了原图像的人物轮廓,无法得出原图像的细节信息,其加密效果是最优的。
2、直方图分析
以下从图像的直方图来分析像素位置与像素值双重置换加密的有效性,原图像图5(a)的直方图如图6(a)所示,只经过像素位置置换的加密密图图5(b)的直方图如图6(b)所示,而只经过像素值置换的加密密图图5(c)的直方图则如图6(c)所示,图6(d)为经过像素位置与像素值双重置换的加密密图图5(d)的直方图。

从以上实验数据可以得出:基于混沌的数字图像像素位置的加密技术只是置换数字图像的像素点的位置,而像素值并不置换,从而数字图像的直方图不会改变,因而所得密图直方图与原数字图像的直方图相同;而基于混沌的数字图像的像素值加密技术虽然将像素值进行置换,改变了数字图像的直方图,但是像素位置没有置换,因此加密效果不太理想;然而基于混沌的数字图像像素位置与像素值双重置换加密算法既置换像素位置,又置换像素值,从而加密密图的直方图与原图像的直方图是不同的,而且加密后的直方图分布非常均匀,从而加密效果更优。
3、密钥敏感性分析
本文加密算法其本质是利用Logistic混沌序列对像素位置和像素值进行置换,因此在加密和解密过程中不会失真。而且由于是基于Logistic混沌序列,这使得解密对密钥具有极强的敏感性。图7(a)是原图像,图7(b)是使用正确密钥解密的效果图(其密钥与图5中的加密密钥一致),图7(c)是使用错误密钥对密图进行像素值解密的效果图,所使用的像素值解密密钥为u0=3.891,x0=0.91211,图7(d)则是使用错误密钥对密图再进行像素位置解密的效果图,所使用的像素位置加密密钥为u0=3.911,x0=0.89111。以上实验数据充分表明本文所提出的加密算法对密钥具有极强的敏感性,密钥相差极微,却仍然不能解密,而且这种错误密钥解密后的图像不具有原图像的任何信息,因此算法安全性是很高的。
本文加密算法的密钥为K=(x0,u0),x0可以取(0,1)之间的任何值,其密钥空间无穷大,而且加密过程中应用了多个混沌序列,更极大地增加了密钥空间。使得整个加密算法既有较好的加密效果,又有较强的安全性。从而,对密钥的穷举攻击变得不可行。
本文加密算法中都是采用二维数组存储数字图像,其大小为m×n,本加密算法主要的运算是对序列排序和对像素位置和像素值置换,而对序列排序算法的时间复杂度为0(n2),对像素位置和像素值进行置换的运算就是根据已经排序好的序列的对应关系而对二维数字图像数组进行取值和赋值运算,因而其时间复杂度亦为0(n2),因此本文提出的加密算法的总时间复杂度为0(n2)。而目前的图像加密算法都维持在这个数量级上,所以本文加密算法其运算效率是比较理想的。
小知识之像素
“像素”(Pixel)是由Picture(图像)和Element(元素)这两个单词的字母所组成的,是用来计算数码影像的一种单位,如同摄影的相片一样,数码影像也具有连续性的浓淡阶调,我们若把影像放大数倍,会发现这些连续色调其实是由许多色彩相近的小方点所组成,这些小方点就是构成影像的最小单位“像素”(Pixel)。











